ELF abstracts page
SPEAKERS : please add below, in your own section, your title talk and abstract :
- first : log in;
- click on your name in the "Contents" box below, this will lead you to your own section;
- your section starts with your name as the title line, click on [edit] (far right).
- >>> How to insert a picture in your abstract
The order of abstracts follow the program of the workshop.
E. Alikhani
Address
Title of the talk
Abstract...
References
[1]
[2]
P. C. Hiberty
Université de Paris-Sud, Laboratoire de Chimie Physique, UMR8000, 91405 Orsay Cédex, France
New Concepts in Chemical Bonding. Charge-Shift Bonding and its Manifestations in Chemistry
Abstract:
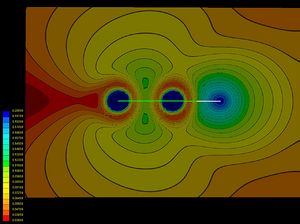
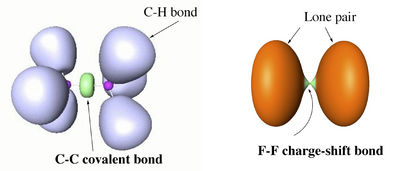
Valence bond (VB) theory and electron-localization function (ELF) calculations of various single bonds demonstrate that along the two classical bond families of covalent and ionic bonds, there exists a class of charge-shift bonds (CS-bonds) in which the fluctuation of the electron pair density plays a dominant role. In VB theory, CS-bonding manifests by large covalent-ionic resonance energy, and in ELF by a depleted basin population with large variances (fluctuations).[1]
CS-bonding can be found in homopolar as well as heteropolar bonds. Atoms that are prone to CS-bonding are compact electronegative and/or electron rich species. An extreme case is the single bond in difluorine, where the purely covalent wave function is repulsive at all distances, while the stability of the molecule is entirely due to covalent-ionic resonance.
The difference between covalent and charge-shift bonds, in terms of ELF picture, is illustrated with the examples of ethane and F2 below.
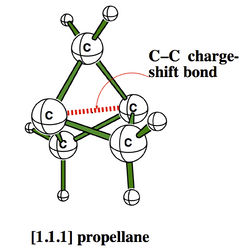
The CS character of such bonds have some experimental consequences, among which the strange stabilities of some cage compounds like the family of propellanes, which display rather strong bonds between “inverted” carbons despite their pyramidalization in the “wrong” direction.[2]
Another experimental consequence, the rarity of silicenium ions in condensed phases,[3] will be addressed if there is some time left.
References
[1] S. Shaik, D. Danovich, B. Silvi, D.L. Lauvergnat, P.C. Hiberty, Chem. Eur. J. 2005, 11, 658.
[2] S. Shaik, D. Danovich, W. Wu, P. C. Hiberty, Nature Chem. 2009, 1, 443.
[3] P. Su, L. Song, W. Wu, S. Shaik, P. C. Hiberty, J. Phys. Chem. A 2008, 112, 2988.
C. Lepetit
Laboratoire de Chimie de Coordination UPR 8241 CNRS, 205, Route de Narbonne, F-31077 Toulouse cedex 05. France.
ELF analysis, an outstanding tool for characterization of chemical bonding, electron delocalization and reactivity.
ELF analysis is now recognized as an oustanding tool for the description of chemical bonding, especially in challenging situations such as multicentric bonds, donor-acceptor bonds, distinction between ionic or weakly covalent interactions ....
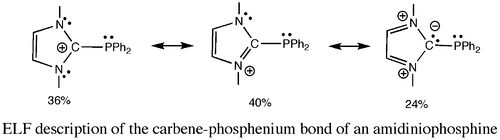
Recent examples in the carbo-mer chemistry [1] or in the coordination chemistry of strong donating carbon ligands such as phosphonium ylides and yldiides [2] or poorly electron-donating amidiniophosphines will be discussed to illustrate the large extent of ELF analysis applications :
(i) In conjugated systems, translation of ELF populations and covariances into weights of most representative mesomeric forms allows for the characterization of electron delocalization and aromaticity [3].
(ii) ELF analysis may be combined to fragment orbital analysis to describe metal-ligand electron transfer in terms of donation and back-donation contributions within the framework of the Dewar-Chatt-Duncanson model [4].
(iii) ELF analysis allows for the prediction of chemical reactivity. Fukui indices and dual descriptors [5] condensed on ELF basins can indeed be used to identify the most sensitive sites where electrophilic or nucleophilic attack is favored [6].
References
[1] M. Gicquel, J.-L. Heully, C. Lepetit, R. Chauvin Phys. Chem. Chem. Phys. 2008, 10, 3578.
[2] R. Zurawinski, Y. Canac, C. Lepetit, M. Mikolajczyk, R. Chauvin Inorg. Chem. 2009, 48, 2147.
[3] (a) C. Lepetit, B. Silvi, R. Chauvin J. Phys. Chem. A 2003, 107, 464. (b) B. Silvi, Phys. Chem. Chem. Phys. 2004, 6, 256.
[4] J.-M. Ducéré, C. Lepetit, B. Silvi, R. Chauvin Organometallics 2008, 27, 5263.
[5] C. Morell, A. Grand, A. Toro-Labbe J. Phys. Chem. A 2005, 109, 205.
[6] W. Tiznado, E. Chamorro, R. Contreras, P. Fuentealba J. Phys. Chem. 2005, 109, 3220.
M. Yanez
Departamento de Química, C-9. Universidad Autónoma de Madrid. Cantoblanco, 28049-Madrid. Spain
ELF as a useful tool to understand chemical bonding in challenging cases
Quite unexpectedly, substituent effects on the structure of iminoboranes are opposite to those observed for the acetylene derivatives in spite of the fact that both series of compounds are isoelectronic. [1] More importantly these dissimilarities cannot be easily explained in terms of the atoms in molecules (AIM) theory or in terms of the population of the πBN* or πCC* antibonding orbitals. In some molecules a decrease (increase) of the electron density is unexpectedly reflected in a shortening (lengthening) of the bond. Conversely, the ELF analysis offers a clear picture of the substituent effects on the CC and BN bonding. The dissimilarities between acetylene- and iminoborane derivatives are primarily a consequence of the strong electronegativity difference between the B and N atoms in the iminoboranes. This difference is the origin of the significant distortion of the BN bonding electron density in iminoboranes, which is not seen in the corresponding acetylene analogues.
References
[1] O. Mó; M. Yáñez; A. Martín Pendás; J.E. Del Bene; I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys. 9, 3970 (2007)
B. de Courcy
CNRS,UPMC Univ Paris 06, UMR 7616, Laboratoire de Chimie Théorique, case courrier 137, 4 place Jussieu, F-75005, Paris, France,
Hard and soft cations within large biological systems: an ELF study
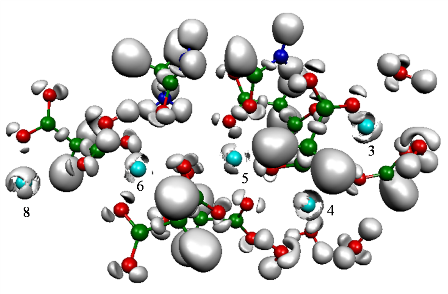
Metal cations exhibit a specific topological signature when studying the electronic localization of their interacting density with biological ligands. Introducing the concept of “subvalence”, for the metal cations, we show that, each cation is able to split the density of its electronic outer shell into “subvalent” domains (or basins) according to its ability to form either partially covalent bonding with their environment for the soft cations, or mainly electrostatic interactions for the hard cations.
We use QCT (Quantum Chemical Topology) techniques such as (QT)AIM and ELF, to study the selectivity of the cations Ca(II) and MG(II), within enzymes involved in the blood coagulation process (the GLA domains of three coagulation factors) [1]. We demonstrate that the enzymatic activity of these proteins is directly linked to the ability of calcium to structure their geometries into their active forms, whereas the presence of magnesium, in addition with calcium, enhances the affinity of the GLA domain for the cellular membrane. We then study the active site of ADH (Alcohol Dehydrogenase), a zinc metalloprotein, to evidence the nature of the interaction of the cation with its ligands [2] as well as the redistribution of the electronic densities of the ligands’ lone pairs under the influence of the cation. We introduce here the notion of “hard” and “soft” ligands[3].
References
[1] de Courcy, B., Pedersen, L. G., Parisel, O., Gresh, N., Silvi, B., Pimé, J., Piquemal, J-P. J. Chem. Theory. Comput. 2010, 6, 1048.
[2] de Courcy B., Dognon J-P., Clavaguéra C., Gresh N., Piquemal J-P. Int J Quantum Chem 2010, in press.
[3] de Courcy B., Gresh N., Piquemal J-P. Interdiscip Sci Comput Life Sci 2009 1, 55.
H. Jamet
Laboratoire Chimie Théorique, DCM, 301 Rue de la Chimie,Domaine Universitaire, 38041 Grenoble Cedex 9, email: hjamet@ujf-grenoble.fr
ELF and MESP : two efficient methods to validate a QM/MM partition for the modelization of Phosphine ligands
A fundamental question that arises after the decision of using QM/MM methods for a certain problem, is how to partition the system, which atoms are going to be included in the QM region and which atoms are going to be included in the MM region? Chemical knowledge is most of the time the guiding line for this choice, but tests should be run in case of uncertainty. In this study we discuss the modelization of phosphine ligands commonly used in the assymetric Pauson-Khand reaction[1] by means of QM/MM methods. X-ray structures of the ligands bound to the tungsten penta(tetra) carbonyl were used as starting point for all calculations. For the evaluation of the position of the QM/MM border, different approaches were used. Firstly, we compare the results of geometry optimizations obtained from ONIOM method using different QM-MM borders with those obtained from full quantum mechanical calculations. Secondly, we evaluate the molecular electrostatic potential (MESP) and the ELF function for the ligand alone, without optimizing it. More precisely we calculate the minimum value of the MESP around the lone pair region of the phosphorus atom as Suresh et al. done[2] and evaluate the population of the valence phosphorus basin V(P). We show that these two later approaches which have the advantage of being fast and computationally inexpensive reproduce the same trend than results obtained from geometry optimizations of the whole complex.
References
[1] K. Hiroi, T. Watanabe, R. Kawagishi and I. Abe. Tetrahedron: Asymmetry, 2000, 11:1197.
[2] J.Mathew, T. Thomas and C.H.Suresh, Inorg. Chem. 2007, 46(25):10800.
G. A. Cisneros
Department of Chemistry, Wayne State University, Detroit, MI, 48202
Topological analysis of the active site of human DNA polymerase lambda provides insight on metal ion mutagenicity in DNA synthesis
DNA polymerases are crucial players in genome replication and repair. They require two divalent metal ions in the active site for catalysis. Experimentally it has been confirmed that the most probable metal ion utilized by polymerases in vivo is Mg(II) [1]. Other metal ions have been shown to be potent mutagens or inhibitors [2]. We have employed ELF analysis based on ab initio quantum mechanical/molecular mechanical (QM/MM) methods to study human DNA polymerase lambda with different metals (Na(I), Ca(II), Co(II), Cr(II), Cu(II), Mg(II), Mn(II), Ni(II) and Zn(II)) in the active site. Our results indicate that all considered mutagenic metals show a split of their outer-shell density, on the recently proposed subvalent domain [3]. This split of the subvalence density is not observed for the non-mutagenic Mg(II) cation. The behavior of the metal subvalence density is directly correlated to its hard or soft character. Distributed electrostatic moments have also been determined to gain a deeper understanding of the electronic polarization.
References
[1] A. Kornberg, T.A. Baker (1992) DNA Replication 2nd Ed., Freeman, San Francisco, CA.
[2] M.A. Sirover, L.A. Loeb, Science, 1976, 194:1434-1426.
[3] B. de Courcy, L. G. Pedersen, O. Parisel, N. Gresh, B. Silvi, J. Pilmé and J-P Piquemal, J. Chem. Theory. Comput., 2010, 6:1048-1063.
X. Assfeld
Xavier Assfeld and Adèle Laurent
Chimie et Biochimie Théoriques, UMR 7565 Nancy Université. email
ELF analysis of core-ionized and core-excited states
Describing core-excited or core-ionized states of macromolecules represent three challenges for theoretical chemistry. The first one is known as the variational collapse which always gives the lowest energy in a given symmetry. The second one is the orthogonality constrain between the ground and the excited/ionized states. The third and last one, is the representation of macromolecule at the quantum mechanical level.
All these three points are related to the fulfillment of orthogonality constrains with respect to given spinorbitals. I will present two methods taking the orthogonality constrains into account differently. The first one modifies the basis functions, the second one changes the Fock operator.
Illustrative calculations will be presented and the electronic structures analyzed by means of ELF analysis.
References
[1] Application of the LSCF Method to Core-Ionized and Core-Excited Molecules, Polymers, and Proteins. True Orthogonality Between Ground and Excited States. N. Ferré et X. Assfeld, J. Chem. Phys. 117 (2002) 4119.
[2] Core-ionized and core-excited states of macromolecules. P.-F. Loos et X. Assfeld, Int. J. Quant. Chem. 107, 12 (2007) 2243-2252
[3] Doubly, triply and multiply excited states from a constrained optimized effective potential method. V. Glushkov and X. Assfeld, J. Chem. Phys. 132, (2010) 204106.
H. S. Rzepa
Department of Chemistry, Imperial College London, email: rzepa@imperial.ac.uk
ELF and the Nature of Triple bonds
A recent report of the species HOS≡CH by Schreiner, Mloston and co-workers1 speculated upon the nature of the SC bond; did it have triple significant bond character? Of the various techniques these authors used for the analysis, neither QTAIM nor ELF was employed. I initially filled this gap by a post on my blog2, and followed this by a full article submitted for publication more conventionally3. The results of this investigation will be presented at the workshop, including a rather surprising conclusion regarding the nature of triple bonds themselves in relation to the degree of charge-shift character they display4. The hypothesis so generated was then extended to investigating the nature of metal-metal multiple bonds, particularly Cr-Cr whose compounds are purported to exhibit homonuclear quadruple or quintuple bonds5. These systems also appear to sustain remarkably high charge-shift character and most intriguing ELF behaviour. The issue for discussion in the workshop is therefore whether or not ELF (combined with QTAIM) is indeed revealing something new about the nature of the triple and higher order homonuclear (metal) bond.
The talk will appear @www.ch.ic.ac.uk/rzepa/talks/elf10 and will feature rotatable ELF isosurfaces and models.
References
[1] P. R. Schreiner, H. P. Reisenauer, J. Romanski, and G. Mloston, Angew. Chemie. 2009, 48, 8133-8136. DOI: 10.1002/anie.200903969
[2] H. S. Rzepa, Blog and follow up
[3] H. S. Rzepa, submitted for publication, 2010.
[4] S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nature Chem., 2009, 1, 443-449. DOI: 10.1038/nchem.327
[5] For initial speculations, see blog.
P. J. MacDougall
Department of Chemistry, Middle Tennessee State University, Murfreesboro, Tennessee, USA
Probing electron correlation in momentum-space
Electron localization is a core concept in chemistry and electronic materials. Prior to the introduction of ELF, practical applications of this concept relied on arbitrary orbital transformation schemes, or averaging electron correlation properties over atomic volumes or other domains. We will review some pre-ELF probes of electron localization, with an emphasis on the utility of the Laplacian of the charge density as an interpretive tool. Complementary analyses are considered for a similar tool operating in momentum-space. The result is unexpected insight into the correlated electron dynamics of molecules that are nano-scale analogs of electronic devices.[1]
References
[1] MacDougall, P. J. and Levit, M. C. "A Synthesis of Fluid Dynamics and Quantum Chemistry in a Momentum-Space Investigation of Molecular Wires and Diodes", in "Computational Studies, Nanotechnology, and Solution Thermodynamics of Polymer Systems", M. D. Dadmun, A. Van Hook, Y. Melnichenko, D. Noid and R. Sumpter (eds.), Kluwer Academic, pp. 139 - 150 (2000).
J. G. Ángyán
CRM2, CNRS & Nancy-University, B.P. 70239, F-54506 Vandoeuvre-lès-Nancy, FRANCE
Fuzzy Wannier-center representation of electron localization: the haystack function
Point-wise characterization of electron localization/delocalization by different variants of the electron localization function (ELF) have proven their usefulness to understand various features of the electronic structure. These functions are usually defined as dimensionless quantities and do not carry any direct, visual information about the population of the localization domains.
Based on the recently established charge density reconstitution rule of the exchange-correlation hole [1]
it is possible to construct a new function, which has the dimension of charge density and preserves the reconstitutes the molecular dipole moment components and, in the mean time, has maxima located at the centroids of the electron pairs. The new function, which has be named haystack function, since it collects
the charge associated to electron pairs, like hay is raked in haystacks, can be regarded also as a fuzzy
variant of the Wannier-center [2] representation of the electron pairs.
References
[1] Gori-Giorgi, P.; Ángyán, J.G.; Savin A., Can. J. Chem. 87, 1444 (2009)
[2] Marzari N.; Vanderbilt, D., Phys. Rev. B. 56, 12847 (1996)
M. Causa
Dipartimento di Chimica, Universita' di Napoli "Federico II", mauro.causa@unina.it
A journey with ELF and probability analysis from atoms, through molecules and nano-systems, to surfaces and crystals
The potential relevance of nano-system is underlined in every branch of sciences.Often assumptions about peculiar electronic properties of nano-systems are invoked. Advanced methods of density and wave-function analysis like ELF can give new light on this field. We will describe a project devoted to the application of these methods to series of systems relevant in catalysis,like nano-structured metals and ionic compounds.
J. Contreras-García
Dept. of Chemistry, Duke University
Non covalent interactions from electron density
Identifying the intricate non covalent interactions patterns in molecules, and especially macromolecules constitutes a crucial step in many areas of biochemistry, including design of ligands, self-assembled materials, catalysts, drugs, and other molecular systems. Current methods either lack generality and/or are difficult to apply to large systems.
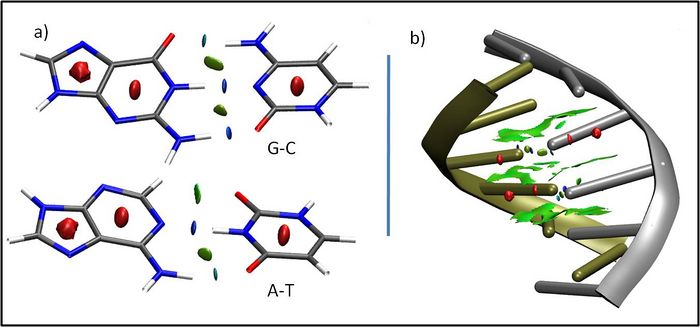
We have developed an index, named NCI, to detect non covalent interactions in real space. It is applicable to both SCF and promolecular densities, so that it only requires knowledge of the atomic coordinates and it is highly efficient in large systems, such as proteins or DNA[1]. NCI provides a rapid and rich representation of van der Waals interactions (vdW), hydrogen bonds (HB), and steric clashes as low-gradient-low-density isosurfaces. Figs. 1a-b shows one such example for the different non covalent interactions appearing in DNA. Colours coding is as follows: HBs are in blue, vdW interactions in green and steric clashes in red. The interactions between individual deoxyadenosine-deoxythymidine and deoxycytidine-deoxyguanosine are highlighted in Figure 1a. It can be seen that NCI is able to reveal the stronger nature of N-H-O vs C-H-O interactions. The large green regions are indicative of π-stacking between base-steps (Fig. 1b).
Across numerous applications of NCI, a view of non bonded interactions emerges as continuous surfaces rather than close contacts between atom pairs, providing insight into the multiple small contribution to macromolecular interaction. Recent results have shown that integration of the density within NCI regions is able to uniquely characterize the strength of interaction. It thus provides a fast and accurate evaluation of the most relevant interactions to biological systems. This tool hence offers exciting possibilities for high throughput screening of drugs and ligand design.
Source code soon available at www.chem.duke.edu/~yang/software.htm
References
[1] E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen, and W. Yang, J. Am. Chem. Soc., 2010, 132 (18), pp 6498–6506. pubs.acs.org/doi/abs/10.1021/ja100936w
D. L. Cooper
Department of Chemistry, University of Liverpool, Liverpool L69 7ZD, UK
Is domain-averaged Fermi hole analysis critically dependent on the choice of atoms-in-molecules domains?
A large number of applications have shown how the analysis of so-called domain-averaged Fermi holes (DAFHs) appears to extract highly visual information about electronic structure and bonding from one- and two-electron density matrices. Somewhat worryingly, even the qualitative form of the geometry dependence of a related quantity, variously known as the shared-electron distribution index (SEDI) or delolocalization index (DI), turns out to be highly sensitive to the choice of atoms-in-molecules method for defining the domains. Together with Patrick Bultinck (Ghent) and Robert Ponec (Prague) we have been investigating whether DAFH analysis might also be so sensitive. Fortunately we find that the DAFH eigenvectors remain very similar for all of the AIM methods considered; the corresponding eigenvalues are found to differ significantly but, importantly, the sums of complementary eigenvalues tend to show only relatively small changes.
References
[1] P. Bultinck, D.L. Cooper and R. Ponec, J. Phys. Chem. A (in press). DOI: 10.1021/jp101707w
A. Lüchow
Institut fuer Physikalische Chemie, RWTH Aachen university, Landoltweg 2, 52056 Aachen, Germany
Single electron densities based on correlated wavefunctions and ELF
A new method is presented based on the partitioning of the total electron density into single electron densities. The partitioning is obtained directly from the squared many-electron wave function by assignment of electron arrangements to the maximum of the squared wave function. In this way, the single electron densities are strongly localized and mainly shaped by the antisymmetry of the many-electron wave function, similar to the ELF basins. The single electron densities are calculated using quantum Monte Carlo techniques. First examples of this analysis are presented: the relationship to the electron pairs of the VSEPR model, the electron structure of aromatic molecules and the analysis of the unusual properties of chemical bonds such as in the fluorine dimer.
E. P. Fowe
Université de Sherbrooke, Departement de Chimie, bvd de l'Université de Sherbrooke, J1k-2R1 Sherbrooke, Canada
Theoretical Study of Ionization and Harmonic Generation on CO2, OCS and CS2 by Ultrashort Intense Laser Pulses: ELF as tool for visualization
In the present work, non pertubative time dependent density theory,TDDFT, methods as opposed to linear response TDDFT are used to study the orientational dependence of ionization and molecular high order harmonic generation, mHOHG, in CO2, OCS, CS2 molecules as a function of laser intensity, I0 ≥ 1014 W/cm2 for few cycle 800 nm laser pulses. A time series analysis is used to confirm the recollision model in MHOHG. We find that at equilibrium distance and at intensities I0 > 3.5x1014 W/cm2, lower highest occupied molecular orbitals, HOMO’s, contribute significantly to ionization and to the mHOHG process. This is due to the symmetry of these orbitals. Even though such lower orbitals have higher ionization potentials, IP, ionization and mHOHG processes occur when orbital densities are maximum with laser polarization direction. Our simulations also reveal that the direction of laser polarization, θ, with respect to the molecular axis of the linear molecule can have a significant effect on mHOHG. At some angles, ionization probabilities of different orbital cross in magnitude. So, while maxima (constructive) and minima (destructive) due to intramolecular interference are found in the dependence of the harmonic intensities magnitude on the orientation of the asymmetric OCS molecule, only maxima interference are found for symmetric CS2 and CO2 molecules when the laser polarization is perpendicular to the molecular axis. These findings are confirmed with the time dependent electron localization function, TDELF, representation through the analysis in term of perturbation appearing on the images of each molecule
References
[1] E. Penka and A. Bandrauk, PRA 81, 023411 (2010)
[2] E. Penka and A. Bandrauk, Can. J. Chem. 87(7): 1081 (2009)
[3] E. Runge and E. K. U. Gross, PRL. 52, 997–1000 (1984)
[4] T. Burnus, M. A. L. Marques and E. K. U. Gross, PRA. 71, 010501(R) (2005)
S.J. Grabowski
Kimika Fakultatea, Euskal Herriko Unibertsitatea, 20080 San Sebastian and IKERBASQUE, Basque Foundation for Science, 48011, Bilbao, Spain
Categories of hydrogen bonds - ELF, QTAIM and other approaches
The ELF definition of hydrogen bonding was introduced [1,2] and it was also found that the analysis of localization domains allows to categorize such interactions into sub-classes [1,2]. This diversification is in line with the other classifications based on the other approaches. For example, the characteristics of Quantum Theory of ´Atoms in Molecules´ (QTAIM) were applied by Rozas and coworkers [3] to classify hydrogen bonds into strong, moderate and weak ones. The latter classification is based on the signs of QTAIM parameters: laplacian of the electron density at the bond critical point (BCP) and the total electron energy density at BCP, but not on the arbitrarily chosen values. Considerning the energetic parameters one can also perform the similar classifications [4,5]. It seems that the decomposition schemes of the interaction energy [6] are useful to characterize hydrogen bonding.
References
[1] Fuster, F.; Silvi, B. Theor.Chem.Acc 2000, 104, 13.
[2] Alikhani, M.E.; Fuster, F.; Silvi, B. Structural Chemistry 2005, 16, 203.
[3] Rozas I, Alkorta I, Elguero J. J.Am.Chem.Soc. 2000, 122, 11154.
[4] Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Chem.Rev. 2005, 105, 3513.
[5] Grabowski, S.J.; Sokalski, W.A.; Dyguda, E.; Leszczynski, J. J.Phys.Chem. B 2006, 110, 6444.
[6] Pendás, A.M.; Blanco, M.A.; Francisco, E. J. Chem. Phys. 2006, 125, 184112.
A. Martín Pendás
Dpto. Química Física y Analítica. Universidad de Oviedo. Spain'
ELF: electron-electron interactions, electron number statistics.
The use of lectron localization functions has provided important insights in theoretical chemistry, including vivid images of chemically important regions. However, integration of operator densities over ELF basins other than electron populations has not been fully exploited up to now. Here we report two examples of non-standard ELF basin integration. On the one hand we show how the electron repulsion energy between basins is able to recover the Gillespie-Nyholm rule within the VSEPR model.1 On the other, we show a number of examples of the full statistics of the electron population distribution functions (EDF) computed over ELF basins.
[1]A. Martín Pendás, E. Francisco, M. A. Blanco, Chem. Phys. Lett. 454, 396 (2008).
E. Matito
Institute of Physics, University of Szczecin, Poland
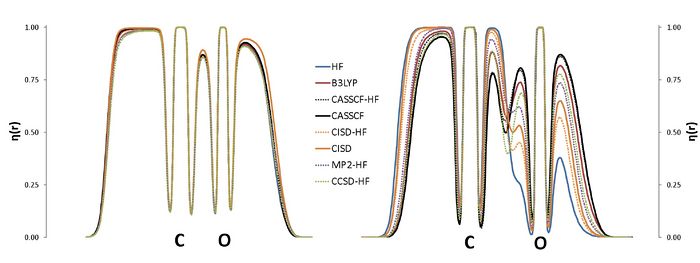
The Electron Localization Function at the Correlated Level: A Natural Orbital Formulation.
The ELF is nowadays used in a wide context, with applications on aromaticity, chemical bonding or reaction mechanisms. The calculation of the ELF involves the computation of the two-particle density (2-PD),1 which has a very simple structure in the case of monodeterminantal wavefunctions. In the case of correlated wavefunctions, the structure of the 2-PD imposes an important bottleneck for both the calculation of the ELF and the population analysis (variance, covariance) of the ELF basins. Therefore, in practice, the use of the ELF for correlated wavefunctions is limited to very small molecules. However, it is possible to lower the numerical complexity of the calculation of the localization function as well as that of the pair populations using approximated expressions for the calculation of 2-PD. In this work we propose a correlated version of the ELF where the 2-PD has been approximated by the formula for the monodeterminantal wavefunctions (X-HF in the graph below) and the formula of Müller in terms of natural orbitals.3,4 The approximation has been tested in a set of molecules, NH3, CO2, H2O, CO, CN-, NO+, N2, H2O2, F2 and FCl-, which have been calculated using a plethora of methods: HF, B3LYP, MP2, CISD, CCSD and CASSCF. The present approach aims at a correlated version of the ELF which can be used in medium size molecules.
References
[1] Matito E., Silvi B., Duran M. and Solà M., J. Chem. Phys. 125, 024301 (2006)
[2] Feixas F., Matito E., Duran M., Solà M. and Silvi B., in preparation.
[3] Müller A.M.K., Phys. Lett. 105A, 446 (1984)
[4] M. A. Buijse, E. J. Baerends, Mol. Phys., 100, 401 (2002)
D. Borgis
Pôle de Physico-Chimie Théorique, UMR-CNRS 8640, Ecole Normale Supérieure et Université Pierre et Marie Curie, 24 rue Lhomond, 75231 Paris Cedex
Classical density functional theory: A theoretical chemist view.
We draw a comparison between the quantum density functional theory for electronic structure calculations and the classical density functional theory (cDFT) of molecular liquids and we show how, borrowing ideas and techniques from electronic DFT, classical DFT can be used as a useful chemist's tool to provide, at a microscopic level, the solvation properties of molecular surfaces or molecular solutes in molecular solvents. This includes the determination of absolute solvation free-energies, as well as three-dimensional microscopic solvation structures. We will show a few applications to solvation in acetonitrile and premises in water. The fundamental object to be considered in cDFT being the solvent position and orientation density around a given molecular solute, we will end by wondering whether their is an equivalent of the ELF function in classical DFT.
References
[1] Rosa Ramirez, Ralph Gebauer, Michel Mareschal, and Daniel Borgis, Phys. Rev. E, 66, 031206 (2002).
[2] Rosa Ramirez and Daniel Borgis, J. Phys. Chem B 109, 6754 (2005).
[3] Rosa Ramirez, Michel Mareschal, and Daniel Borgis, Chem. EssaysExperts.Com is the company which first and main priority was, is and will be customers� satisfaction with the essays online. If you still have no idea where to buy your writing tasks, this company is the best option for you. Phys. 319, 261 (2005).
[4] Lionel Gendre, Rosa Ramirez, and Daniel Borgis, Chem. Phys. Lett. 474, 366 (2009).
R. Vuilleumier
Pôle de Physico-Chimie Théorique, UMR-CNRS 8640, Ecole Normale Supérieure et Université Pierre et Marie Curie, 24 rue Lhomond, 75231 Paris Cedex
From ELF to ALF?
In this short communication, we will discuss how the ideas developed for localizing electrons can find extensions in molecular simulations for the localization of atoms in solvation shells. We will illustrate this by studying the local structure of liquid water using maximum probabilility bassins inspired from Quantum Monte Carlo calculations [1]. Future applications for the study of liquid structure and dynamics will be discussed.
References
[1] A. Scemama,M. Caffarel, A. Savin, Maximum probability domains from Quantum Monte Carlo calculations, J. Comp. Chem. 28, 442 (2007).
J. Cioslowski
Address
Title of the talk
Abstract...
References
[1]
[2]
R. Nesper
Reinhard Nesper Laboratory of Inorganic Chemistry ETH Zürich
Zintl-Phases and Intermetallics – 20 Years with ELF
For nearly 90 year Zintl phases were thought to be electronically well-behaved compound, contrary to intermetallics which need specific treatment theoretical treatment until today. The first ELF analyses of bonding in Zintl compounds starting in 1990 fostered that picture for a while with some hidden specials being undetected.
At the same time, ELF opened many insights into the rich variety of bonding patterns of intermetallics. The development of special ELF tools like space separation and integration models allowed for a better quantification and even prediction of what holds peculiar structures together. Now, as more and finer details of collective interactions come into focus, ELF may play an advanced role both on in subtle detail and with a general scope.
Y. Grin
Max-Planck-Institut für Chemische Physik fester Stoffe, Dresden, Germany
My ELF days in Stuttgart: electron localizability and intermetallic compounds
Due to strongly application governed development of the knowledge on intermetallic compounds, the understanding of their nature is still not complete. Important open questions are: why some intermetallic compounds only form at distinct compositions, why do other they form homogeneity ranges, why some structural motifs are stable and can be often found, why others appear very rarely among intermetallic compounds. One of the reasons for this situation is insufficient knowledge about chemical bonding in intermetallic compounds [1]. The local environment of atoms in the crystal structures of intermetallic compounds is difficult to describe by means of traditional MO pictures as well as by means of the free electron gas model. The atomic coordination is usually more complex as in the inorganic compounds and not necessary can be derived from the closest sphere packing motifs characteristic e.g. for structure of elemental metals. The electron localization – electron density approach has been recently grown into a useful chemical tool for investigating the bond formation in compounds with typically metallic physical properties. Originally defined by Becke and Edgecombe in the framework of Hartree-Fock theory [2] and developed later by Savin et al. for density functional theory [3], the electron localization function (ELF) belongs to the so-called bonding indicators in the positional space. As it was shown by Kohout [4,5], the functions of this group trace the correlation of electronic motion of same-spin electrons and a more general function of this kind is developed called electron localization indicator (ELI). ELF and ELI represent, in general sense, a charge distribution of electron pairs and, thus are suitable tools for analysis of chemical bonding in sense of the Lewis theory, where the pair formation plays the central role. Not only the number of electron localizability functional maxima in the inner shells of a given atom but also the electronic population per shell is very close to the values expected from the Aufbau principle [6,7]. The maxima of electron localizability functional in the valence region (outer shells) provide signatures for directed (covalent) bonding in the position space [8-11]. An application of electron localizability – electron density approach opens the possibility of getting access to bond definition in real space and of electron counting for intermetallic compounds [11-15].
References
[1] Yu. Grin. Wissenschaftl. Z. TU Dresden 49 (2000) 16.
[2] A. D. Becke, K. E. Edgecombe. J. Chem. Phys. 92 (1990) 5397.
[3] A. Savin et al. Angew. Chem. 104 (1992) 185.
[4] M. Kohout. Int. J. Quantum Chem. 97 (2004) 651.
[5] M. Kohout, Faraday Disscuss. 2007, 135, 43-54
[6] M. Kohout, A. Savin. Int. J. Quant. Chem 60 (1996) 875.
[7] A. Savin, B. Silvi, F. Colonna, Can. J. Chem. 1996, 74, 1088.
[8] B. Silvi, A. Savin. Nature 371 (1994) 683.
[9] A. Savin et al. Angew. Chem. 109 (1997) 1892.
[10] F. R. Wagner, V. Bezugly, M. Kohout, Yu. Grin, Chem. Eur. J. 2007, 13, 5724-5741
[11] J. Contreras-Garcia, A. M. Pendas, J. M. Recio, B. Silvi. J. Chem. Theor. Comp. 5 (2009) 164.
[12] E. Dashjav et al. J. Solid State Chem. 181 (2008) 3121.
[13] P. S. Chizhov et al. Z. Anorg. Allg. Chem. 635 (2009) 1863.
[14] O. Sichevych et al. Inorg. Chem. 48 (2009) 6261.
[15] 1F. Haarmann et al. Chem. Eur. J. 15 (2009)1673.
[16] For more details see http://www.cpfs.mpg.de/ELI.
J-F. Halet
Laboratoire Sciences Chimiques de Rennes, UMR 6226 CNRS-Université de Rennes 1, Avenue du Général Leclerc, F-35042 Rennes, France
Elf at Rennes. What do we do with it in solid-state chemistry? Examples in boride carbide and boride silicide chemistry
Solid state rare-earth metal boride carbides show an amazing diversity of stoichiometries and exhibit an astonishing variety of stable architectures. These architectures can be systematized by several arrangements of the non-metal sub-structures, ranging from zero-dimensional units isolated from each other in a matrix of metal atoms to one- and two-dimensional networks alternating with metal sub-lattices, which are closely related to the electron count per light atoms, boron and carbon [1-3]. Interestingly, the chemistry of rare-earth metal–boron–silicon does not parallel that of rare-earth metal–boron–carbon. B–C bonds are easily formed in the latter, leading to a large variety of different structural arrangements, whereas Si–B bonds are hardly observed in the former, except in insertion compounds [3]. Parameters such as the symmetry, the electron count of the non-metal sub-structures and the nature of the rare-earth metals will be analyzed with the aid of density-functional band structure calculations and the electron localization function (ELF) to address the issues of bonding, structural arrangement and physical properties of some representative compounds.
References
[1] J. Bauer, J.-F. Halet, J.-Y. Saillard, Coord. Chem. Rev. 178–180 (1998) 723–753 and refs. therein.
[2] J.-F. Halet, in: M.G. Davidson, A.K. Hugues, T.B. Marder, K. Wade (Eds.), Contemporary Boron Chemistry, Royal Society of Chemistry, Cambridge, 2000, p. 514 and refs. therein.
[3] M. Ben Yahia, J. Roger, X. Rocquefelte, R. Gautier, J. Bauer, R. Guérin, J.-Y. Saillard, J.-F. Halet, J. Solid State Chem. 179 (2006) 2779–2786 and refs. therein.
U. Wedig
Max Planck Institute for Solid State Research, Heisenbergstr. 1, 70569 Stuttgart, Germany
ELF in electron deficient clusters
The analysis of the Electron Localization Function in closo boron clusters [1] was one of the first applications on compounds containing non-Lewis structures. In this class of electron deficient compounds, which can be well described by Wade's rules, the 2n+2 skeletal electrons lead to reducible ELF domains with the form of the dual polyhedron of the boron cage. Such an ELF pattern can be related to resonance structures containing n+1 3-center-2-electron and/or 2-center-2-electron bonds.[2,3]
The knowledge about the bonding characteristics of boron cluster, however, can not be reliably applied to clusters of the heaviest non-synthetic homologue element, thallium. The high speed of the electrons near the nucleus requires a relativistic description of the system and results in the formation of inert electron pairs. As a consequence, in some cases the formal electron count for Tl clusters in solid state compounds is lower than required by Wade's rules for closo clusters. One example is the recently found [Tl8]6- cluster in Cs18Tl8O6, the first homoatomic, covalently bonded cluster with the shape of a tetrahedral star or stella quadrangula.[4] The cluster has 2n-2 skeletal electrons, being best denoted as hypoelectronic.[5] In the ELF of this cluster, only features related to the inert electron pair can be identified (Fig. 1).
Remarkably, an isoelectronic cluster with the different shape of a parallelepiped was previously found in Cs8Tl8O.[6] Both clusters can be derived from an homocubane unit by displacive distortions. Relativistic DFT calculations including spin-orbit coupling show, that the parallelepiped is the result of a Jahn-Teller distortion. In contrast, the electronic structure of the tetrahedral star can be only described in accordance with the diamagnetic behavior of the Cs18Tl8O6 compound if spin-orbit coupling is considered.
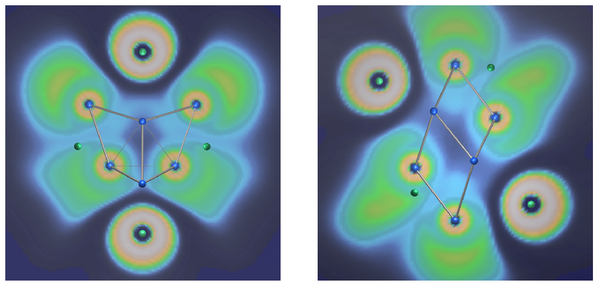
References
[1] A. Burkhardt, U. Wedig, H. G. von Schnering, A. Savin, Z. Anorg. Allg. Chem. 619 (1993) 437.
[2] A. Savin, R. Nesper, S. Wengert, T. F. Faessler, Angew. Chem. 109 (1997) 1893, Angew. Chem. Int. Ed. 36 (1997) 1809.
[3] T. F. Faessler, A. Savin, Chemie in unserer Zeit 31 (1997) 110.
[4] U. Wedig, V. Saltykov, J. Nuss, M. Jansen, J. Am. Chem. Soc., submitted.
[5] J. D. Corbett, Angew. Chem. 112 (2000) 682, Angew. Chem. Int. Ed. 39 (2000) 670.
[6] A. Karpov, M. Jansen, Angew. Chem. 117 (2005) 7813, Angew. Chem. Int. Ed. 44 (2005) 7639.
R. Weihrich
University of Ulm, Institute of Inorganic Chemistry II Materials and Catalysis, Albert-Einstein-Allee 11 D-89081 Ulm (Germany) Fon: +49 (0)731/50-23867 or/- 22575 (secretary) Fax: +49 (0)731/50-23039
Bonding in Half Antiperovskites
Compounds with the composition A2M3X2 was recently described as half antiperovskites (HAP) AM3/2X as shown for InNi3/2S [1], BiPd3/2S [2], PbNi3/2S [3], and ARh3/2S (A = In, Sn, Tl, Pb, Bi) [4]. Within the structural concept, the crystal structures are easily deduced from antiperovskites like MgNi3C by occupation of only half of the M = Ni sites. The symmetry of e.g. trigonal PbNi3/2S, monoclinic BiNi3/2S, and kubic BiPd3/2S is completely determined by M site ordering. As structural relations were drawn to [Hg3S2]Cl2 and K2[Sn2O3] the question is now asked if half antiperovskites can be written by the general formula A2[M3S2] with covalent M-S networks that are indicated by short atomic distances. To enlight chemical bonding of range of HAP compounds, ELF and AIM analysis were performed based on DFT all electron calculations. Comparison is given to bonding in hard compounds of light elements [5].
References
[1] R. Weihrich, I. Anusca, M. Zabel, Z. Anorg. Allg. Chem., 631 (2005) 1463. [2] R. Weihrich, I. Anusca, Z Anorg Allg Chem. 632 (2006) 335. [3] R. Weihrich, S.F. Matar, V. Eyert, F. Rau, M. Zabel, M. Andratschke, I. Anusca, T. Bernert, Prog. Solid State Ch., 35 (2007) 309. [4] I. Anusca, A. Schmid, Ph. Peter, J. Rothballer, F. Pielnhofer, R. Weihrich: Z. Anorg. Allg. Chem. 635 (2009) 2410. [5] R. Weihrich, S.F. Matar, E. Betranhandy, V. Eyert, Solid State Sci. 5 (2003) 701. R. Weihrich, S. F. Matar, E. Betranhandy, J. Phys. Chem. Solids. 64 (2003) 1539.
P. Raybaud
IFP, Direction Catalyse et Séparation, Département Catalyse par les Sulfures, Rond-point de l'échangeur de Solaize BP 3 - 69360 Solaize - France. Mail
From electronic to catalytic properties of transition metal sulfides
This talk will illustrate how density functional theory (DFT) calculations has helped to make new progresses in the atomic scale understanding of the active sites of transition metal sulfides materials, widely used in industrial catalytic reactions. In particular, the surface energy calculation of the MoS2 based catalysts makes possible to solve the equilibrium morphology of Co (and Ni) promoted MoS2 nano-particles [1,2]. Valence and core electronic properties solved by DFT calculations are successfully compared to experimental scanning tunnel microscopy [1] and X-ray photoelectron spectroscopy [3]. In agreement with the ELF analysis of of the chemical interaction (figure 1) [4], the adsorption energy of organic molecules explains the catalytic behavior of these materials [5].
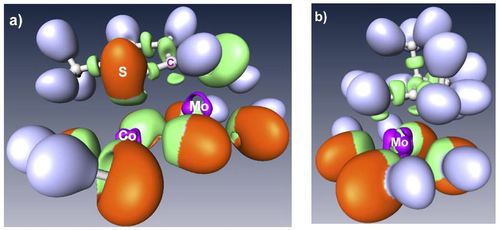
References
[1] H. Schweiger, P. Raybaud, H. Toulhoat, J. Catal. 212, 33-38 (2002).
[2] E. Krebs, B. Silvi, P. Raybaud, Catal. Today 130, 160-169 (2008).
[3] A.D. Gandubert, E. Krebs, C. Legens, D. Costa, D. Guillaume, P. Raybaud, Catal. Today 130, 149-159 (2008).
[4] E. Krebs, B. Silvi, P. Raybaud, J. Chem. Theory and Comput. 5, 580-593 (2009).
[5] E. Krebs, B. Silvi, A. Daudin, P. Raybaud, J. Catal. 260, 276–287 (2008).
N. Chéron
ENS de Lyon, Laboratoire de Chimie, 46 allée d'Italie, 69364 Lyon Cedex 07
Computational study of the Nef reaction : study of the mechanism, influence of parameters and extension of the reaction
When old reactions are looked in the light of modern tools, new understandings can be acquired, leading to new results. In this presentation, we will focus at the Nef-insertion reaction of isocyanides with acyl chlorides forming imidoyl chlorides, first described 120 years ago [1].
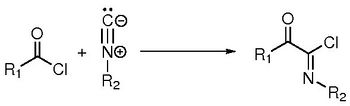
We first showed that this reaction proceeds via a new kind of mechanism between a nucleophile species and an acid derivative, which occurs in one elementary step (and not a two-step addition-elimination mechanism). It is close to the Sn2 mechanism of acyl chlorides hydrolysis.
We then investigated effects of variations on the solvent, the acyl chloride, the isocyanide or the chlorine moitey on the energy profile. We were able to reproduce experimental results. For example, we found that the reaction is faster with acyl bromide, acyl iodide or methyl-oxalylchloride. More, we also found a linear correlation between the activation energy and the lone pair population of the carbonyl oxygen (computed via ELF analysis, see V(O) in Figure below). This correlation opens up the application field of this reaction.
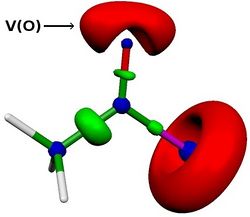
References
[1] Nef, J. U. Justus Liebigs Ann. Chem. 1892, 270, 267
J. Pilmé
Laboratoire de Chimie Théorique, UMR7616 UPMC-Univ. Paris 06 / CNRS
Distributed Electrostatic Moments using the ELF partition: a tool for the bonding analysis?
- The ELF partition of the total charge density allows computing of local moments located at non atomic centers such as lone pairs and bonds. The local moments are used to rationalize covalent interactions as well as typical hydrogen bond interactions. Bond quadrupole polarization moments being related to a pi character enable to discuss bond multiplicities, and to sort families of molecules according to their bond order. Transferability tests show that the approach is probably suitable for the design of advanced force fields.
References
[1] Advancing beyond Charge Analysis using the Electronic Localization Function: Chemically Intuitive Distribution of Electrostatic Moments. J. Pilmé and J-P Piquemal. J. Comp. Chem., 29(9), 2008 , 1440-144
S. Berski
Address
Title of the talk
Abstract...
References
[1]
[2]
H. Gérard
Laboratoire de Chimie Théorique, UMR7616 UPMC-Univ. Paris 06 / CNRS
Theoretical Tools to Understand Organic Chemistry: Case of Carbanion Chemistry
Formation of new C-C bond has been for many years and still remains a challenge to organic chemists. Among the various synthetic solutions envisioned, many rely on carbanions or carbanion equivalents such as organometallic complexes. A major difficulty in using these species lies in the selectivity for formation and reaction of these species: when various sites can be deprotonated or when the negative charge can be delocalized, the nucleophilic site can migrate on the carbon chain of the reactant, leading to problems in mastering the regioselectivity of the reaction.
Significant help to the synthetic chemist can be obtained from theoretical investigation. A classical approach relies in computing the relative stability of the various tautomeric forms or of the metallotropic equilibrium, or in computing the various regiodiffering reaction paths. An other possibility is to resort to the various tools developed by theoretical chemists to analyse the energetic properties or electronic structure of the reactants. Among them, the topoplogical analysis of the Electron Localization Function (ELF) is especially attractive as it can be easily connected to a Lewis structure. In particular, it allows quantitative evaluation of the inductive [1] or mesomeric [2] effects usually used in organic chemistry to justify for the stabilisation of negative charges.
We will propose some examples of the application of such methods to the description of the electronic structure of highly delocalized carbanions and to the understanding of the various factors affecting their reactivity.
References
[1] “How the topological analysis of the electron localization function accounts for the inductive effect”, I. Fourré, H. Gérard, B. Silvi, J. Mol. Struc.: THEOCHEM, 2007, 811, 69-76.
[2] “Sulfonyl vs. carbonyl group: which is the more electron-withdrawing” I. Chataigner, C. Panel, H. Gérard, S. Piettre, Chem. Commun., 2007, 3288-3290.
L. Joubert
IRCOF, Université de Rouen, 1 rue Tesnière, 76130 Mont Saint-Aignan
Making density functional theory and the quantum theory of atoms in molecules converse: a local approach
A first (local) bridge between Kohn–Sham density functional theory and the quantum theory of atoms in molecules of Bader is built by means of a second order reduced density gradient expansion of the exchange-correlation energy density at a given bond critical point [1]. This approach leads to the definition of new “mixed” descriptors that are particularly useful for the classification of the chemical interactions for which the traditional atoms in molecules characterization reveals insufficient, as for instance the distinction between hydrogen and agostic bonds.
Reference
[1] V. Tognetti, L. Joubert and C. Adamo, J. Chem. Phys. 132, 211101 (2010)
H. Bolvin
Laboratoire de Chimie Quantique 4 rue Blaise Pascal 67000 Strasbourg
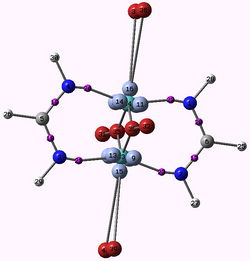
Bond length effect in the spectrochemical series. Magnetic coupling and metal-metal bond.
For a transition metal complex, the ligand field parameter is defined within an octahedral environment as the splitting energy Delta separating the t2g from the eg set of nd orbitals. Comparing Delta for a range of different ligands, one finds that the order is essentially independent of the metal ion, as long as the oxidation state, coordination geometry and spin states are kept constant. In halide complexes, Delta decreases according to the sequence F->Cl->Br->I-. This series is usually interpreted using pi-effects. Down the column, the electronegativity decreases which favorizes both sigma- and pi-interactions. But, simultaneously, the ionic radius and consequently the bond length increase. Despite of this bond lengthening, the covalence of the bond increases in the series in the sense that the global charge transfer from ligand to metal increases. But pi-interactions decrease because they are more sensible to distance than sigma-ones and the destabilization of the antibonding orbitals decreases because ligand orbitals are more and more diffuse down the column; with diffuse orbitals, the charge transfer is made easier but does not contribute as much to a gain of energy.
The [Li6Ca2Mn2N6] crystal presents magnetic properties with a large antiferromagnetic coupling between two spins S=1. It shows a direct Mn-Mn bond with Mn atoms in d3 configuration. We will show that the magnetic coupling is due to the coupling of the pi electrons localized on each metallic center via the delocalized sigma electrons following spin polarization mechanism.
'References
[1] H. Bolvin Eur. J. Inorg. Chem. 2010 2221 (2010).
[2] ``H. Bolvin, F. R. Wagner, W. Schnelle, R. Kniep. manuscript in preparation
A. de la Lande
Laboratoire de Chimie Physique, CNRS UMR 8000
Université Paris-Sud 11
aurelien.de-la-lande@u-psud.fr
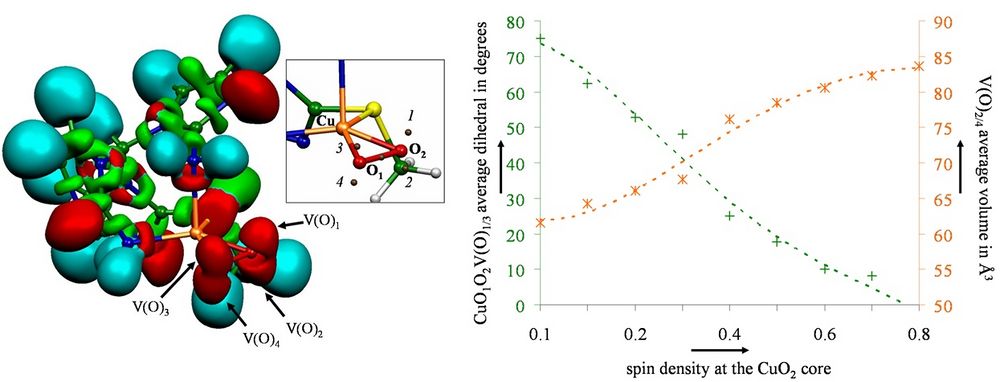
Constrained DFT and ELF Analysis
Constrained Density Functional Theory (CDFT) is a computational tool enabling one to access the diabatic description of a molecular electronic structure in opposite to regular DFT that provides an adiabatic representation. It other words one can impose a charge or spin density on a group of atoms within a molecular system during the DFT computation. To achieve this goal a constraining potential term is added to the Hamiltonian and its amplitude is optimized on-the-fly during the SCF procedure so that the converged electronic density fulfills the desired charge repartition.
This approach has been originally proposed by Q. Wu and T. Van Voorhis[1] and we have recently implemented it in the DFT code deMon2k.[2] Moreover we have also recently interfaced the CDFT approach to the ELF topological analysis. In our presentation we will briefly give some details about the underlying CDFT methodology, but we will essentially show some applications of our approach to the case of a copper dioxygen adduct
References
[1] Q. Wu, T. Van Voorhis, "Direct optimization method to study constrained systems within density-functional theory" Phys. Rev. A, 2005, 72, 024502
[2] A. de la Lande, D. R. Salahub, "Derivation of interpretative models for long range electron transfer from constrained density functional theory" J. Mol. Strcut. THEOCHEM, 2010, 943, 115
R. Nalewajski
Department of Theoretical Chemistry and Department of Computational Methods in Chemistry, Faculty of Chemistry, Jagiellonian University, R. Ingardena 3, 30-060 Cracow, Poland
Use of Non-Additive Fisher-Information in Probing the Chemical Bonds
In chemistry an adequate identification of chemical bonds in complicated molecular systems is of paramount importance for both structural and reactivity purposes. In the past various local probes have been suggested for exploring the calculated molecular electron distributions in chemical terms, such as the bonding and lone-electron pairs, etc. For example, the Electron Localization Function (ELF) [1] have been shown to provide attractive tools for visualizing such structural building-blocks of the system electronic structure [2-4]. Alternatively, the bond-multiplicity indices formulated in both the MO and Orbital Communication theories can be used to quantify the bond-“connectivities” between bonded atoms [4-14]. The ELF concept has been shown to explore the non-additive part of the Fisher information in the Molecular Orbital (MO) resolution [15], while a similar approach in the Atomic Orbital (AO) representation [4,16] gives rise to the Contra-Gradience (CG) criterion [14,16-19], related to the AO representation of the electronic kinetic-energy operator, to explore the chemical bonds in the molecule. This AO-phase sensitive index is capable of distinguishing the bonding, non-bonding, and anti-bonding electronic states in H2, as do the off-diagonal Charge and Bond-Order (CBO) matrix elements of quantum chemistry. It successfully locates the bonding basins of the physical space corresponding to the negative non-additive Fisher information density in the AO resolution, thus qualitatively answering the fundamental question about the existence or non-existence of the chemical bond(s) between a given pair of constituent atoms and providing the visual representation of the bonding region in question. The main purpose of this talk is to introduce this “ELF for chemical bonds” concept and to present illustrative applications of this novel, local probe of chemical bonds in generating the associated visual and quantitative descriptors.
The contra-gradience (CG) criterion is related to the non-additive Fisher information and kinetic energy of electrons in the resolution determined by the basis-functions χ = {χi} of the standard SCF LCAO MO calculations of molecular electronic structure, e.g., Atomic-Orbitals (AO). It can be used used to locate the bonding regions in space and to generate the associated quantitative information-theoretic (IT) descriptors of these localized chemical bonds in molecules. The key quantity is the interference (non-additive, delocalization) contribution to the molecular Fisher-information density, fnadd.[χ; r] = f total[χ; r] − f add.[χ; r], where f total[χ; r] ≡ f total[ρ; r] stands for the molecular (overall) distribution for the molecular ground-state density ρ, and f add.[χ; r] = ∑i f[χi; r] denotes its AO-additive part. The CG criterion identifies the regions of the physical space exhibiting a diminished overall Fisher information content, compared to the reference AO-additive level. This scalar field is used to determine the bonding basins in the molecule, identified as the valence, closed volumes of fnadd.[χ; r] < 0 or f total[χ; r] < f add.[χ; r], enclosed by the zero CG surface fnadd.[χ; r] = 0. These bonding volumes represent a locally decreased gradient content of the system wave-function, thus reflecting less “order” (more “uncertainty”) in the molecular distribution of electrons marking their relative delocalization via the system chemical bonds.
The CG concept will be first illustrated in the simplest two-orbital model of H2. The graphical representations of both the closed bonding and core areas of a diminished CG density will be presented for illustrative molecules, together with the associated numerical IT descriptors measuring the associated integrals of fnadd.[χ; r] over the volumes in question. These examples convincingly validate the applicability of the CG probe in exploring the bonding pattern in molecules from the Fisher-information/kinetic-energy perspective at the AO level of resolution.
The majority of theoretical interpretations of the origins of the covalent chemical bond emphasizes exclusively the potential (interaction) aspect of this phenomenon, focusing on the mutual attraction between the accumulation of electronic density between the two bonded atoms (a negative “bond-charge”) and the partially screened (positively charged) nuclei. The CG, electron-delocalization probe, reflecting the non-additive component in the AO resolution of the molecular Fisher information, adopts the complementary view by stressing the importance of the kinetic-energy component of the chemical bonds.
[1] A. D. Becke, K. E. Edgecombe, J. Chem. Phys. 92 (1990) 5397.
[2] A. Savin, R. Nesper, S. Wengert, T.F. Fässler, Angew. Chem. Int. Ed. Engl. 36 (1997) 808; B. Silvi, A. Savin, Nature 371 (1994) 683.
[3] R. F. Nalewajski, Information Theory of Molecular Systems, Elsevier, Amsterdam, 2006;
[4] R. F. Nalewajski, Information Origins of the Chemical Bond, Nova Science Publishers, New York, 2010.
[5] R. F. Nalewajski, D. Szczepanik, J. Mrozek, Adv. Quant. Chem., in press.
[6] K. A. Wiberg, Tetrahedron 24 (1968) 1083.
[7] M. S. Gopinathan, K. Jug, Theor. Chim. Acta (Berl.) 63 (1983) 497, 511
[8] I. Mayer, Chem. Phys. Lett. 97 (1983) 270.
[9] R. F. Nalewajski, A. M. Köster, K. Jug, Theoret. Chim. Acta (Berl.) 85 (1993) 463.
[10] R. F. Nalewajski, J. Mrozek, Int. J. Quantum Chem. 51 (1994) 187.
[11] R. F. Nalewajski, S. J. Formosinho, A. J. C. Varandas, J. Mrozek, Int. J. Quantum Chem. 52 (1994) 1153.
[12] R. F. Nalewajski, J. Mrozek, G. Mazur, Can. J. Chem. 100 (1996) 1121.
[13] R. F. Nalewajski, J. Mrozek, A. Michalak, Int. J. Quantum Chem. 61 (1997) 589.
[14] J. Mrozek, R. F. Nalewajski, A. Michalak, Polish J. Chem. 72 (1998) 1779.
[15] R. F. Nalewajski, Chem. Phys. Lett. 386 (2004) 265.
[16] R. F. Nalewajski, A. M. Köster, S. Escalante, J. Phys. Chem. A 109, 10038 (2005).
[17] R. F. Nalewajski, Int. J. Quantum Chem. 108 (2008) 2230.
[18] R. F. Nalewajski, P. de Silva, J. Mrozek, Kinetic Energy Functional, A. Wang, T. Wesołowski, Eds, World Scientific, Singapore, 2009, in press.
[19] R. F. Nalewajski, J. Math. Chem. 47 (2010) 667.
[20] R. F. Nalewajski, , P. de Silva, J. Mrozek, THEOCHEM, in press.
J. Tao
Los Alamos National Laboratory, Los Alamos, New Mexico 87545
Quantum Stress in Descriptive Chemistry
In this talk, I will discuss the construction of a physically-motivated electron localization function. Then I will discuss how to include quantum many-body effects -- the exchange-correlation contribution [1]. Finally, I will discuss a recent work on the ELF for systems exposed to a magnetic field.
References
[1]
A. Scemama
Laboratoire de Chimie et Physique Quantiques / IRSAMC, Toulouse (France)
Localizing electron pairs with the Electron Pair Localization Function
The Electron Pair Localization Function gives a direct measure of the degree of pairing of electrons in a molecule. Its value is positive in the case of anti-parallel electron pairing, negative in the case of parallel electron pairing, and close to zero when the electrons are unpaired. Therefore --as with the ELF-- chemical bonds, core domains and lone pairs can be visualized. However, unpaired electrons exhibit minimum values and can be easily differenciated from electron pairs.
References
[1] Electron pair localization function, a practical tool to visualize electron localization in molecules from quantum Monte Carlo data
A. Scemama, P. Chaquin, M. Caffarel
J. Chem. Phys., vol 121, pp. 1725-1735 (2004)
[2] Structural and optical properties of a neutral Nickel bisdithiolene complex. Density Functional versus ab-initio methods.
F. Alary, J.-L. Heully, A. Scemama, B. Garreau-de-Bonneval, K. I. Chane-Ching, M. Caffarel
Theoretical Chemistry Accounts, in press