Différences entre les versions de « ELF abstracts page »
| Ligne 719 : | Ligne 719 : | ||
[5] R. F. Nalewajski, D. Szczepanik, J. Mrozek, Adv. Quant. Chem., in press. | [5] R. F. Nalewajski, D. Szczepanik, J. Mrozek, Adv. Quant. Chem., in press. | ||
| − | [ | + | [6] K. A. Wiberg, Tetrahedron 24 (1968) 1083. |
| − | [ | + | [7] M. S. Gopinathan, K. Jug, Theor. Chim. Acta (Berl.) 63 (1983) 497, 511 |
| − | [ | + | [8] I. Mayer, Chem. Phys. Lett. 97 (1983) 270. |
| − | [ | + | [9] R. F. Nalewajski, A. M. Köster, K. Jug, Theoret. Chim. Acta (Berl.) 85 (1993) 463. |
| − | [ | + | [10] R. F. Nalewajski, J. Mrozek, Int. J. Quantum Chem. 51 (1994) 187. |
| − | [ | + | [11] R. F. Nalewajski, S. J. Formosinho, A. J. C. Varandas, J. Mrozek, Int. J. Quantum Chem. 52 (1994) 1153. |
| − | [ | + | [12] R. F. Nalewajski, J. Mrozek, G. Mazur, Can. J. Chem. 100 (1996) 1121. |
| − | [ | + | [13] R. F. Nalewajski, J. Mrozek, A. Michalak, Int. J. Quantum Chem. 61 (1997) 589. |
| − | [ | + | [14] J. Mrozek, R. F. Nalewajski, A. Michalak, Polish J. Chem. 72 (1998) 1779. |
| − | [ | + | [15] R. F. Nalewajski, Chem. Phys. Lett. 386 (2004) 265. |
| − | [ | + | [16] R. F. Nalewajski, A. M. Köster, S. Escalante, J. Phys. Chem. A 109, 10038 (2005). |
| − | [ | + | [17] R. F. Nalewajski, Int. J. Quantum Chem. 108 (2008) 2230. |
| − | [ | + | [18] R. F. Nalewajski, P. de Silva, J. Mrozek, Kinetic Energy Functional, A. Wang, T. Wesołowski, Eds, World Scientific, Singapore, 2009, in press. |
| − | [ | + | [19] R. F. Nalewajski, J. Math. Chem. 47 (2010) 667. |
| − | [ | + | [20] R. F. Nalewajski, , P. de Silva, J. Mrozek, THEOCHEM, in press. |
''' | ''' | ||
Version du 25 mai 2010 à 14:35
SPEAKERS : please add below, in your own section, your title talk and abstract :
- first : log in;
- click on your name in the "Contents" box below, this will lead you to your own section;
- your section starts with your name as the title line, click on [edit] (far right).
- >>> How to insert a picture in your abstract
The order of abstracts follow the program of the workshop.
E. Alikhani
Address
Title of the talk
Abstract...
References
[1]
[2]
P. C. Hiberty
Université de Paris-Sud, Laboratoire de Chimie Physique, UMR8000, 91405 Orsay Cédex, France
New Concepts in Chemical Bonding. Charge-Shift Bonding and its Manifestations in Chemistry
Abstract:
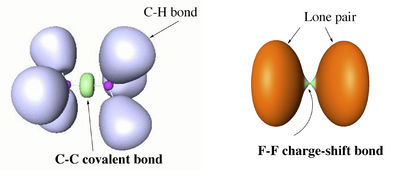
Valence bond (VB) theory and electron-localization function (ELF) calculations of various single bonds demonstrate that along the two classical bond families of covalent and ionic bonds, there exists a class of charge-shift bonds (CS-bonds) in which the fluctuation of the electron pair density plays a dominant role. In VB theory, CS-bonding manifests by large covalent-ionic resonance energy, and in ELF by a depleted basin population with large variances (fluctuations).[1]
CS-bonding can be found in homopolar as well as heteropolar bonds. Atoms that are prone to CS-bonding are compact electronegative and/or electron rich species. An extreme case is the single bond in difluorine, where the purely covalent wave function is repulsive at all distances, while the stability of the molecule is entirely due to covalent-ionic resonance.
The difference between covalent and charge-shift bonds, in terms of ELF picture, is illustrated with the examples of ethane and F2 below.
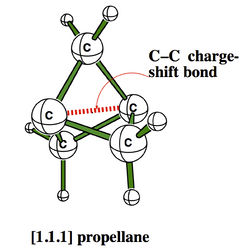
The CS character of such bonds have some experimental consequences, among which the strange stabilities of some cage compounds like the family of propellanes, which display rather strong bonds between “inverted” carbons despite their pyramidalization in the “wrong” direction.[2]
Another experimental consequence, the rarity of silicenium ions in condensed phases,[3] will be addressed if there is some time left.
References
[1] S. Shaik, D. Danovich, B. Silvi, D.L. Lauvergnat, P.C. Hiberty, Chem. Eur. J. 2005, 11, 658.
[2] S. Shaik, D. Danovich, W. Wu, P. C. Hiberty, Nature Chem. 2009, 1, 443.
[3] P. Su, L. Song, W. Wu, S. Shaik, P. C. Hiberty, J. Phys. Chem. A 2008, 112, 2988.
C. Lepetit
Address
Title of the talk
Abstract...
References
[1]
[2]
M-M. Rohmer
Address
Title of the talk
Abstract...
References
[1]
[2]
B. De Courcy
Address
Title of the talk
Abstract...
References
[1]
[2]
H. Jamet
Laboratoire Chimie Théorique, DCM, 301 Rue de la Chimie,Domaine Universitaire, 38041 Grenoble Cedex 9, email: hjamet@ujf-grenoble.fr
ELF and MESP : two efficient methods to validate a QM/MM partition for the modelization of Phosphine ligands
A fundamental question that arises after the decision of using QM/MM methods for a certain problem, is how to partition the system, which atoms are going to be included in the QM region and which atoms are going to be included in the MM region? Chemical knowledge is most of the time the guiding line for this choice, but tests should be run in case of uncertainty. In this study we discuss the modelization of phosphine ligands commonly used in the assymetric Pauson-Khand reaction[1] by means of QM/MM methods. X-ray structures of the ligands bound to the tungsten penta(tetra) carbonyl were used as starting point for all calculations. For the evaluation of the position of the QM/MM border, different approaches were used. Firstly, we compare the results of geometry optimizations obtained from ONIOM method using different QM-MM borders with those obtained from full quantum mechanical calculations. Secondly, we evaluate the molecular electrostatic potential (MESP) and the ELF function for the ligand alone, without optimizing it. More precisely we calculate the minimum value of the MESP around the lone pair region of the phosphorus atom as Suresh et al. done[2] and evaluate the population of the valence phosphorus basin V(P). We show that these two later approaches which have the advantage of being fast and computationally inexpensive reproduce the same trend than results obtained from geometry optimizations of the whole complex.
References
[1] K. Hiroi, T. Watanabe, R. Kawagishi and I. Abe. Tetrahedron: Asymmetry, 2000, 11:1197.
[2] J.Mathew, T. Thomas and C.H.Suresh, Inorg. Chem. 2007, 46(25):10800.
G. A. Cisneros
Department of Chemistry, Wayne State University, Detroit, MI, 48202
Topological analysis of the active site of human DNA polymerase lambda provides insight on metal ion mutagenicity in DNA synthesis
DNA polymerases are crucial players in genome replication and repair. They require two divalent metal ions in the active site for catalysis. Experimentally it has been confirmed that the most probable metal ion utilized by polymerases in vivo is Mg(II) [1]. Other metal ions have been shown to be potent mutagens or inhibitors [2]. We have employed ELF analysis based on ab initio quantum mechanical/molecular mechanical (QM/MM) methods to study human DNA polymerase lambda with different metals (Na(I), Ca(II), Co(II), Cr(II), Cu(II), Mg(II), Mn(II), Ni(II) and Zn(II)) in the active site. Our results indicate that all considered mutagenic metals show a split of their outer-shell density, on the recently proposed subvalent domain [3]. This split of the subvalence density is not observed for the non-mutagenic Mg(II) cation. The behavior of the metal subvalence density is directly correlated to its hard or soft character. Distributed electrostatic moments have also been determined to gain a deeper understanding of the electronic polarization.
References
[1] A. Kornberg, T.A. Baker (1992) DNA Replication 2nd Ed., Freeman, San Francisco, CA.
[2] M.A. Sirover, L.A. Loeb, Science, 1976, 194:1434-1426.
[3] B. de Courcy, L. G. Pedersen, O. Parisel, N. Gresh, B. Silvi, J. Pilmé and J-P Piquemal, J. Chem. Theory. Comput., 2010, 6:1048-1063.
X. Assfeld
Address
Title of the talk
Abstract...
References
[1]
[2]
H. S. Rzepa
Department of Chemistry, Imperial College London, email: rzepa@imperial.ac.uk
ELF and the Nature of Triple bonds
A recent report of the species HOS≡CH by Schreiner, Mloston and co-workers1 speculated upon the nature of the SC bond; did it have triple significant bond character? Of the various techniques these authors used for the analysis, neither QTAIM nor ELF was employed. I initially filled this gap by a post on my blog2, and followed this by a full article submitted for publication more conventionally3. The results of this investigation will be presented at the workshop, including a rather surprising conclusion regarding the nature of triple bonds themselves in relation to the degree of charge-shift character they display4. The hypothesis so generated was then extended to investigating the nature of metal-metal multiple bonds, particularly Cr-Cr whose compounds are purported to exhibit homonuclear quadruple or quintuple bonds5. These systems also appear to sustain remarkably high charge-shift character and most intriguing ELF behaviour. The issue for discussion in the workshop is therefore whether or not ELF (combined with QTAIM) is indeed revealing something new about the nature of the triple and higher order homonuclear (metal) bond.
The talk will appear @www.ch.ic.ac.uk/rzepa/talks/elf10 and will feature rotatable ELF isosurfaces and models.
References
[1] P. R. Schreiner, H. P. Reisenauer, J. Romanski, and G. Mloston, Angew. Chemie. 2009, 48, 8133-8136. DOI: 10.1002/anie.200903969
[2] H. S. Rzepa, Blog and follow up
[3] H. S. Rzepa, submitted for publication, 2010.
[4] S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nature Chem., 2009, 1, 443-449. DOI: 10.1038/nchem.327
[5] For initial speculations, see blog.
M. Yanez
Departamento de Química, C-9. Universidad Autónoma de Madrid. Cantoblanco, 28049-Madrid. Spain
ELF as a useful tool to understand chemical bonding in challenging cases
Quite unexpectedly, substituent effects on the structure of iminoboranes are opposite to those observed for the acetylene derivatives in spite of the fact that both series of compounds are isoelectronic. [1] More importantly these dissimilarities cannot be easily explained in terms of the atoms in molecules (AIM) theory or in terms of the population of the πBN* or πCC* antibonding orbitals. In some molecules a decrease (increase) of the electron density is unexpectedly reflected in a shortening (lengthening) of the bond. Conversely, the ELF analysis offers a clear picture of the substituent effects on the CC and BN bonding. The dissimilarities between acetylene- and iminoborane derivatives are primarily a consequence of the strong electronegativity difference between the B and N atoms in the iminoboranes. This difference is the origin of the significant distortion of the BN bonding electron density in iminoboranes, which is not seen in the corresponding acetylene analogues.
References
[1] O. Mó; M. Yáñez; A. Martín Pendás; J.E. Del Bene; I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys. 9, 3970 (2007)
P. J. MacDougall
Address
Title of the talk
Abstract...
References
[1]
[2]
J. Angyan
Address
Title of the talk
Abstract...
References
[1]
[2]
M. Causa
Address
Title of the talk
Abstract...
References
[1]
[2]
J. Contreras-Garcia
Address
Title of the talk
Abstract...
References
[1]
[2]
D. L. Cooper
Address
Title of the talk
Abstract...
References
[1]
[2]
A. Lüchow
Address
Title of the talk
Abstract...
References
[1]
[2]
E. P. Fowe
Address
Title of the talk
Abstract...
References
[1]
[2]
S.J. Grabowski
Kimika Fakultatea, Euskal Herriko Unibertsitatea, 20080 San Sebastian and IKERBASQUE, Basque Foundation for Science, 48011, Bilbao, Spain
Categories of hydrogen bonds - ELF, QTAIM and other approaches
The ELF definition of hydrogen bonding was introduced [1,2] and it was also found that the analysis of localization domains allows to categorize such interactions into sub-classes [1,2]. This diversification is in line with the other classifications based on the other approaches. For example, the characteristics of Quantum Theory of ´Atoms in Molecules´ (QTAIM) were applied by Rozas and coworkers [3] to classify hydrogen bonds into strong, moderate and weak ones. The latter classification is based on the signs of QTAIM parameters: laplacian of the electron density at the bond critical point (BCP) and the total electron energy density at BCP, but not on the arbitrarily chosen values. Considerning the energetic parameters one can also perform the similar classifications [4,5]. It seems that the decomposition schemes of the interaction energy [6] are useful to characterize hydrogen bonding.
References
[1] Fuster, F.; Silvi, B. Theor.Chem.Acc 2000, 104, 13.
[2] Alikhani, M.E.; Fuster, F.; Silvi, B. Structural Chemistry 2005, 16, 203.
[3] Rozas I, Alkorta I, Elguero J. J.Am.Chem.Soc. 2000, 122, 11154.
[4] Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Chem.Rev. 2005, 105, 3513.
[5] Grabowski, S.J.; Sokalski, W.A.; Dyguda, E.; Leszczynski, J. J.Phys.Chem. B 2006, 110, 6444.
[6] Pendás, A.M.; Blanco, M.A.; Francisco, E. J. Chem. Phys. 2006, 125, 184112.
A. Martín Pendás
Dpto. Química Física y Analítica. Universidad de Oviedo. Spain'
ELF: electron-electron interactions, electron number statistics.
The use of lectron localization functions has provided important insights in theoretical chemistry, including vivid images of chemically important regions. However, integration of operator densities over ELF basins other than electron populations has not been fully exploited up to now. Here we report two examples of non-standard ELF basin integration. On the one hand we show how the electron repulsion energy between basins is able to recover the Gillespie-Nyholm rule within the VSEPR model.1 On the other, we show a number of examples of the full statistics of the electron population distribution functions (EDF) computed over ELF basins.
[1]A. Martín Pendás, E. Francisco, M. A. Blanco, Chem. Phys. Lett. 454, 396 (2008).
E. Matito
Institute of Physics, University of Szczecin, Poland
The Electron Localization Function at the Correlated Level: A Natural Orbital Formulation.
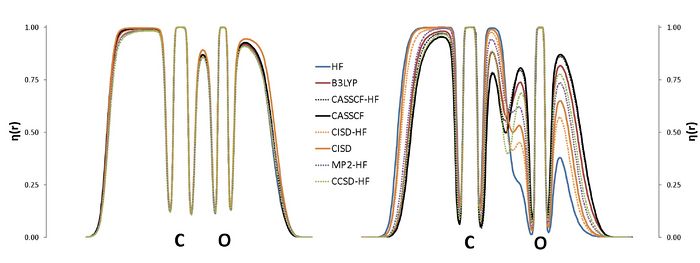
The ELF is nowadays used in a wide context, with applications on aromaticity, chemical bonding or reaction mechanisms. The calculation of the ELF involves the computation of the second-order density matrix (DM2),1 which has a very simple structure in the case of monodeterminantal wavefunctions. In the case of correlated wavefunctions, the structure of the DM2 imposes an important bottleneck for both the calculation of the ELF and the population analysis (variance, covariance) of the ELF basins. Therefore, in practice, the use of the ELF for correlated wavefunctions is limited to very small molecules. However, it is possible to lower the numerical complexity of the calculation of the localization function as well as that of the pair populations using approximated expressions for the calculation of DM2. In this work we propose a correlated version of the ELF where the DM2 has been approximated by the formula for the monodeterminantal wavefunctions (X-HF in the graph below) and the formula of Müller in terms of natural orbitals.3,4 The approximation has been tested in a set of molecules, NH3, CO2, H2O, CO, CN-, NO+, N2, H2O2, F2 and FCl-, which have been calculated using a plethora of methods: HF, B3LYP, MP2, CISD, CCSD and CASSCF. The present approach aims at a correlated version of the ELF which can be used in medium size molecules.
References
[1] Matito E., Silvi B., Duran M. and Solà M., J. Chem. Phys. 125, 024301 (2006)
[2] Feixas F., Matito E., Duran M., Solà M. and Silvi B., in preparation.
[3] Müller A.M.K., Phys. Lett. 105A, 446 (1984)
[4] M. A. Buijse, E. J. Baerends, Mol. Phys., 100, 401 (2002)
D. Borgis
Address
Title of the talk
Abstract...
References
[1]
[2]
R. Vuillemier
Address
Title of the talk
Abstract...
References
[1]
[2]
J. Cioslowski
Address
Title of the talk
Abstract...
References
[1]
[2]
J. Pilmé
Address
Title of the talk
Abstract...
References
[1]
[2]
R. Nesper
Address
Title of the talk
Abstract...
References
[1]
[2]
Y. Grin
Max-Planck-Institut für Chemische Physik fester Stoffe, Dresden, Germany
My ELF days in Stuttgart: electron localizability and intermetallic compounds
Due to strongly application governed development of the knowledge on intermetallic compounds, the understanding of their nature is still not complete. Important open questions are: why some intermetallic compounds only form at distinct compositions, why do other they form homogeneity ranges, why some structural motifs are stable and can be often found, why others appear very rarely among intermetallic compounds. One of the reasons for this situation is insufficient knowledge about chemical bonding in intermetallic compounds [1]. The local environment of atoms in the crystal structures of intermetallic compounds is difficult to describe by means of traditional MO pictures as well as by means of the free electron gas model. The atomic coordination is usually more complex as in the inorganic compounds and not necessary can be derived from the closest sphere packing motifs characteristic e.g. for structure of elemental metals. The electron localization – electron density approach has been recently grown into a useful chemical tool for investigating the bond formation in compounds with typically metallic physical properties. Originally defined by Becke and Edgecombe in the framework of Hartree-Fock theory [2] and developed later by Savin et al. for density functional theory [3], the electron localization function (ELF) belongs to the so-called bonding indicators in the positional space. As it was shown by Kohout [4,5], the functions of this group trace the correlation of electronic motion of same-spin electrons and a more general function of this kind is developed called electron localization indicator (ELI). ELF and ELI represent, in general sense, a charge distribution of electron pairs and, thus are suitable tools for analysis of chemical bonding in sense of the Lewis theory, where the pair formation plays the central role. Not only the number of electron localizability functional maxima in the inner shells of a given atom but also the electronic population per shell is very close to the values expected from the Aufbau principle [6,7]. The maxima of electron localizability functional in the valence region (outer shells) provide signatures for directed (covalent) bonding in the position space [8-11]. An application of electron localizability – electron density approach opens the possibility of getting access to bond definition in real space and of electron counting for intermetallic compounds [11-15].
References
[1] Yu. Grin. Wissenschaftl. Z. TU Dresden 49 (2000) 16.
[2] A. D. Becke, K. E. Edgecombe. J. Chem. Phys. 92 (1990) 5397.
[3] A. Savin et al. Angew. Chem. 104 (1992) 185.
[4] M. Kohout. Int. J. Quantum Chem. 97 (2004) 651.
[5] M. Kohout, Faraday Disscuss. 2007, 135, 43-54
[6] M. Kohout, A. Savin. Int. J. Quant. Chem 60 (1996) 875.
[7] A. Savin, B. Silvi, F. Colonna, Can. J. Chem. 1996, 74, 1088.
[8] B. Silvi, A. Savin. Nature 371 (1994) 683.
[9] A. Savin et al. Angew. Chem. 109 (1997) 1892.
[10] F. R. Wagner, V. Bezugly, M. Kohout, Yu. Grin, Chem. Eur. J. 2007, 13, 5724-5741
[11] J. Contreras-Garcia, A. M. Pendas, J. M. Recio, B. Silvi. J. Chem. Theor. Comp. 5 (2009) 164.
[12] E. Dashjav et al. J. Solid State Chem. 181 (2008) 3121.
[13] P. S. Chizhov et al. Z. Anorg. Allg. Chem. 635 (2009) 1863.
[14] O. Sichevych et al. Inorg. Chem. 48 (2009) 6261.
[15] 1F. Haarmann et al. Chem. Eur. J. 15 (2009)1673.
[16] For more details see http://www.cpfs.mpg.de/ELI.
J-F. Halet
Address
Title of the talk
Abstract...
References
[1]
[2]
U. Wedig
Address
Title of the talk
Abstract...
References
[1]
[2]
R. Weihrich
Address
Title of the talk
Abstract...
References
[1]
[2]
P. Raybaud
Address
Title of the talk
Abstract...
References
[1]
[2]
E. Dumont
Address
Title of the talk
Abstract...
References
[1]
[2]
N. Chéron
Address
Title of the talk
Abstract...
References
[1]
[2]
S. Berski
Address
Title of the talk
Abstract...
References
[1]
[2]
L. Joubert
Address
Title of the talk
Abstract...
References
[1]
[2]
H. Bolvin
Address
Title of the talk
Abstract...
References
[1]
[2]
A. Delalande
Address
Title of the talk
Abstract...
References
[1]
[2]
R. Nalewajski
Department of Theoretical Chemistry and †Department of Computational Methods in Chemistry, Faculty of Chemistry, Jagiellonian University, R. Ingardena 3, 30-060 Cracow, Poland
Use of Non-Additive Fisher-Information in Probing the Chemical Bonds
In chemistry an adequate identification of chemical bonds in complicated molecular systems is of paramount importance for both structural and reactivity purposes. In the past various local probes have been suggested for exploring the calculated molecular electron distributions in chemical terms, such as the bonding and lone-electron pairs, etc. For example, the Electron Localization Function (ELF) [1] have been shown to provide attractive tools for visualizing such structural building-blocks of the system electronic structure [2-4]. Alternatively, the bond-multiplicity indices formulated in both the MO and Orbital Communication theories can be used to quantify the bond-“connectivities” between bonded atoms [4-14]. The ELF concept has been shown to explore the non-additive part of the Fisher information in the Molecular Orbital (MO) resolution [15], while a similar approach in the Atomic Orbital (AO) representation [4,16] gives rise to the Contra-Gradience (CG) criterion [14,16-19], related to the AO representation of the electronic kinetic-energy operator, to explore the chemical bonds in the molecule. This AO-phase sensitive index is capable of distinguishing the bonding, non-bonding, and anti-bonding electronic states in H2, as do the off-diagonal Charge and Bond-Order (CBO) matrix elements of quantum chemistry. It successfully locates the bonding basins of the physical space corresponding to the negative non-additive Fisher information density in the AO resolution, thus qualitatively answering the fundamental question about the existence or non-existence of the chemical bond(s) between a given pair of constituent atoms and providing the visual representation of the bonding region in question. The main purpose of this talk is to introduce this “ELF for chemical bonds” concept and to present illustrative applications of this novel, local probe of chemical bonds in generating the associated visual and quantitative descriptors.
The contra-gradience (CG) criterion is related to the non-additive Fisher information and kinetic energy of electrons in the resolution determined by the basis-functions χ = {χi} of the standard SCF LCAO MO calculations of molecular electronic structure, e.g., Atomic-Orbitals (AO). It can be used used to locate the bonding regions in space and to generate the associated quantitative information-theoretic (IT) descriptors of these localized chemical bonds in molecules. The key quantity is the interference (non-additive, delocalization) contribution to the molecular Fisher-information density, fnadd.[χ; r] = f total[χ; r] − f add.[χ; r], where f total[χ; r] ≡ f total[ρ; r] stands for the molecular (overall) distribution for the molecular ground-state density ρ, and f add.[χ; r] = ∑i f[χi; r] denotes its AO-additive part. The CG criterion identifies the regions of the physical space exhibiting a diminished overall Fisher information content, compared to the reference AO-additive level. This scalar field is used to determine the bonding basins in the molecule, identified as the valence, closed volumes of fnadd.[χ; r] < 0 or f total[χ; r] < f add.[χ; r], enclosed by the zero CG surface fnadd.[χ; r] = 0. These bonding volumes represent a locally decreased gradient content of the system wave-function, thus reflecting less “order” (more “uncertainty”) in the molecular distribution of electrons marking their relative delocalization via the system chemical bonds.
The CG concept will be first illustrated in the simplest two-orbital model of H2. The graphical representations of both the closed bonding and core areas of a diminished CG density will be presented for illustrative molecules, together with the associated numerical IT descriptors measuring the associated integrals of fnadd.[χ; r] over the volumes in question. These examples convincingly validate the applicability of the CG probe in exploring the bonding pattern in molecules from the Fisher-information/kinetic-energy perspective at the AO level of resolution.
The majority of theoretical interpretations of the origins of the covalent chemical bond emphasizes exclusively the potential (interaction) aspect of this phenomenon, focusing on the mutual attraction between the accumulation of electronic density between the two bonded atoms (a negative “bond-charge”) and the partially screened (positively charged) nuclei. The CG, electron-delocalization probe, reflecting the non-additive component in the AO resolution of the molecular Fisher information, adopts the complementary view by stressing the importance of the kinetic-energy component of the chemical bonds.
[1] A. D. Becke, K. E. Edgecombe, J. Chem. Phys. 92 (1990) 5397.
[2] A. Savin, R. Nesper, S. Wengert, T.F. Fässler, Angew. Chem. Int. Ed. Engl. 36 (1997) 808; B. Silvi, A. Savin, Nature 371 (1994) 683.
[3] R. F. Nalewajski, Information Theory of Molecular Systems, Elsevier, Amsterdam, 2006;
[4] R. F. Nalewajski, Information Origins of the Chemical Bond, Nova Science Publishers, New York, 2010.
[5] R. F. Nalewajski, D. Szczepanik, J. Mrozek, Adv. Quant. Chem., in press.
[6] K. A. Wiberg, Tetrahedron 24 (1968) 1083.
[7] M. S. Gopinathan, K. Jug, Theor. Chim. Acta (Berl.) 63 (1983) 497, 511
[8] I. Mayer, Chem. Phys. Lett. 97 (1983) 270.
[9] R. F. Nalewajski, A. M. Köster, K. Jug, Theoret. Chim. Acta (Berl.) 85 (1993) 463.
[10] R. F. Nalewajski, J. Mrozek, Int. J. Quantum Chem. 51 (1994) 187.
[11] R. F. Nalewajski, S. J. Formosinho, A. J. C. Varandas, J. Mrozek, Int. J. Quantum Chem. 52 (1994) 1153.
[12] R. F. Nalewajski, J. Mrozek, G. Mazur, Can. J. Chem. 100 (1996) 1121.
[13] R. F. Nalewajski, J. Mrozek, A. Michalak, Int. J. Quantum Chem. 61 (1997) 589.
[14] J. Mrozek, R. F. Nalewajski, A. Michalak, Polish J. Chem. 72 (1998) 1779.
[15] R. F. Nalewajski, Chem. Phys. Lett. 386 (2004) 265.
[16] R. F. Nalewajski, A. M. Köster, S. Escalante, J. Phys. Chem. A 109, 10038 (2005).
[17] R. F. Nalewajski, Int. J. Quantum Chem. 108 (2008) 2230.
[18] R. F. Nalewajski, P. de Silva, J. Mrozek, Kinetic Energy Functional, A. Wang, T. Wesołowski, Eds, World Scientific, Singapore, 2009, in press.
[19] R. F. Nalewajski, J. Math. Chem. 47 (2010) 667.
[20] R. F. Nalewajski, , P. de Silva, J. Mrozek, THEOCHEM, in press.
A. Scemama
Address
Title of the talk
Abstract...
References
[1]
[2]
J. Tao
Address
Title of the talk
Abstract...
References
[1]
[2]
I. Fourré
Address
Title of the talk
Abstract...
References
[1]
[2]
H. Gérard
Address
Title of the talk
Abstract...
References
[1]
[2]
N. Russo
Address
Title of the talk
Abstract...
References
[1]
[2]