Différences entre les versions de « The SD BOVB method »
| Ligne 32 : | Ligne 32 : | ||
# perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while '''''freezing the inactive orbitals''''' during the optimization (put "0" as coefficient in first $orb line) ; | # perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while '''''freezing the inactive orbitals''''' during the optimization (put "0" as coefficient in first $orb line) ; | ||
# then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while '''''freezing the active orbitals''''' during the optimization (put "0" as coefficient in first $orb line). | # then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while '''''freezing the active orbitals''''' during the optimization (put "0" as coefficient in first $orb line). | ||
| + | |||
| + | As an example, see the SD-BOVB calculation on the F<sub>2</sub> molecule in the tutorial machines here : | ||
| + | |||
| + | EXERCISES/TUTORIAL1/EXERCISE3/question3/answer/.SD-BOVB | ||
| + | |||
| + | We obtain a bonding energy of 37.1 kcal/mol at the SD-BOVB level using the 6-31G(d) basis set, already very close to the estimated exact value of 39.0 kcal/mol. | ||
| + | |||
====High symmetry case:==== | ====High symmetry case:==== | ||
# Perform a π-D-VBSCF calculation '''together with the keyword ''boys'' ''' in the $orb section ; | # Perform a π-D-VBSCF calculation '''together with the keyword ''boys'' ''' in the $orb section ; | ||
Version du 10 juillet 2012 à 15:44
<<< Back to the "general guidelines for BOVB calculations"
Definition of the S-BOVB level
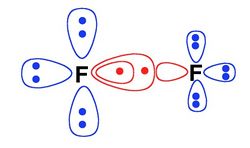
The "S" in the name means "splitted". At this level, in each VB structure, all the active orbitals which are doubly occupied at the L-BOVB level are "splitted", that is to say they are replaced by a pair of singlet-coupled electrons in two different orbitals located on the same center. Here is below a pictorial example for the F-F+ ionic structure of difluorine dimer. This allows the inclusion of some more dynamical correlation (radial correlation) for the active electron pairs.
How to proceed - HF example
To go from the L-BOVB to the S-BOVB level, one will have to start from the converged orbitals obtained at the L-BOVB level as a guess, and then modify it manually by duplicating the active doubly occupied orbitals (split them), and modify them slightly in order to differentiate them (we recommend to operate on the larger basis function coefficient, making it larger in one of the split pair orbital and smaller on the other, in order to make one of these orbital more contracted and the other more diffuse). Then, optimize this wave function by freezing the inactive orbitals.
In order to best understand the procedure, we recommend to look to a simple example like the HF molecule, and compare the L-BOVB definition and .orb file with the S-BOVB definition and .gus file. Corresponding files for the S-BOVB calculation could be found in the tutorial machines here :
EXERCISES/TUTORIAL1/EXERCISE2/question2/answer/.SBOVB
As can be seen in this example, the L-BOVB level, which will directly transfer to a ~5 kcal/mol improvement on the Bond Energy as both L-BOVB and S-BOVB dissociate to H plus F atoms calculated separately at the RHF level in gas phase.
IMPORTANT WARNINGS
- The S-BOVB method is REALLY a Valence Bond expert level. You should have some significant experience with D-BOVB calculations before trying S- and SD-BOVB ones.
- It is EXTREMELY important to start from a good orbital guess, otherwise misconvergence or, more importantly, convergence on secondary minima or unphysical solutions will happens. In particular :
- the "boys" keyword MUST be used at the initial VBSCF level, as it will ensures that the splitted orbital really physically correspond to your active pair, and not an inactive pair sharing the same orbital definition (for instance : to distinguish between the 2s lone pair of Fluorine and the sigma active orbital in F2 or HF molecules).
- a converged L-BOVB solution must be used as a guess for the S-BOVB level
- you should modify the guess orbitals for the splitted pairs intelligently, as a dumb modification usually ends to an unphysical S-BOVB solution
SD-BOVB calculations
General case (low symmetry):
- Perform a ("L") VBSCF calculation together with the keyword boys in the $orb section ;
- perform the L-BOVB calculation, starting from converged VBSCF orbitals ;
- perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while freezing the inactive orbitals during the optimization (put "0" as coefficient in first $orb line) ;
- then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while freezing the active orbitals during the optimization (put "0" as coefficient in first $orb line).
As an example, see the SD-BOVB calculation on the F2 molecule in the tutorial machines here :
EXERCISES/TUTORIAL1/EXERCISE3/question3/answer/.SD-BOVB
We obtain a bonding energy of 37.1 kcal/mol at the SD-BOVB level using the 6-31G(d) basis set, already very close to the estimated exact value of 39.0 kcal/mol.
High symmetry case:
- Perform a π-D-VBSCF calculation together with the keyword boys in the $orb section ;
- perform a π-D-BOVB calculation, starting from converged VBSCF orbitals ;
- perform the π-SD-BOVB calculation in two steps :
- step1 : starting from the converged π-D-BOVB orbitals as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while freezing the inactive orbitals during the optimization (put "0" as coefficient in first $orb line) ;
- step2 : then restarting from the converged orbitals obtained at the previous step, optimizing all orbitals (both active and inactive) at the same time.
As an example, see the π-SD-BOVB calculation on the F2 molecule in the tutorial machines here :
EXERCISES/TUTORIAL1/EXERCISE3/question3/answer/.PI-SD-BOVB
We can see that the bonding energy at the π-D-BOVB is found to be 32.0 kcal/mol using the cc-pVTZ basis set, and it is improved to 36.1 kcal/mol at the π-SD-BOVB.