VBTutorial1

<< Return to the program

Basics of VB theory and XMVB program

Exercise 1 : Starting up with the H<math>{}_2</math> molecule

The Gamess and XMVB input files for the H<math>{}_2</math> molecule are provided in the Exercise folder on the tutorial machines. These are VBSCF calculations with the 6-31G(d,p) basis set, and the fragment specification in terms of symmetry-adapted orbitals (frgtyp=sao).

Just inspect these inputs, run the gamess-xmvb program (using : vbrun h2), and analyze the outputs.

Then these input files could serve you as templates for the next exercises.

Exercise 2 : HF molecule weights

1. Compute a VBSCF three structure wave function for the HF molecule, using the frgtyp=sao specification, automatic guess (guess=auto), and boys keyword in the $tctrl section. Which structure(s) should be kept in further BOVB calculations ?
2. Using VBSCF orbitals as guess orbitals :
   1. Compute a L-BOVB wave function on a selected subset of structures ;
   2. Compute a VBCISD wave function, freezing the 1s core orbital of fluorine in the VBCI calculation (NCOR=1 option), and printing only structures which have a coefficient superior to 0.01 (ctol=0.01 option) ;
   3. Compare structure weights at the VBSCF, L-BOVB and VBCI levels

Hints

To go from L-VBSCF to L-BOVB level, starting from the input of the VBSCF input file (.xmi) as a template, you should simply make the following changes in it : add the bovb keyword in "$ctrl" section ; change iscf=5 by iscf=2 ; suppress structures with minor weights at the VBSCF level from the '$str section use "guess=read" option to read previous converged VBSCF orbitals Then to use L-VBSCF orbitals as guess orbitals, copy the file: file_name-l-vbscf.orb which was created in the VBSCF step, to a new file : file_name-l-bovb.gus. To go from L-VBSCF to the VBCI wave functions, starting from the input of the VBSCF input file as a template, you should simply make the following changes : add the corresponding VBCI keyword in the $ctrl section (VBCISD here) ; use "guess=read" option and previous converged VBSCF orbitals as input.gus guess file

>> general guidelines for BOVB calculations

Exercise 3 : F<math>{}_2</math> molecule and bond energy

1. Compute a L-VBSCF wave function for the F<math>{}_2</math> molecule (all inactive orbitals localized on the fluorine atoms), using:
   • the frgtyp=sao specification, without using the f basis functions in the definition of the fragment orbitals for simplicity ;
   • the boys keyword in the $ctrl section ;
   • automatic guess (guess=auto option) ;
2. Recompute the same L-VBSCF wave-function, this time specifying converged RHF MOs as guess orbitals, through the guess=mo option in the $ctrl section together with an extra $gus section in the input (see hints below, XMVB Manual, and/or Peifeng Su's lecture slides) ;
3. BOVB level :
   1. First, compute a π-D-VBSCF wave function using previous VBSCF orbitals as guess orbitals. To do that, you should allow the π inactive orbitals of fluorine to delocalize onto the two atoms, while keeping all <math>\sigma</math> (active and inactive) orbitals localized (see also : >> see "high symmetry case" in the "general guidelines for BOVB calculations")
   2. Compute then a π-D-BOVB solution for the F<math>{}_2</math> molecule, starting from previous orbitals as guess.
4. VBCI : compute a VBCI(D,S) wave function (vbcids keyword in the $ctrl section), freezing the core orbitals of fluorine in the calculation.
5. Deduce F<math>{}_2</math> bond energies at both the π-D-BOVB and VBCI(D,S) levels.

Hints and remarks

To prepare a $gus section for reading RHF MOs as a guess (guess=mo option) : first compute gamess RHF solution only (take out : vbtyp=xmvb in the $control section of Gamess input) read the RHF orbitals in Gamess and identify those who could be good guess orbitals for your different VB orbitals. For instance : MO n°1 is a symmetry combination for 1s cores of the two Fluorine, so this same MO n°1 could be used as a guess orbital for the two localized VB orbitals corresponding to the fluorine cores (MO n°2 is the corresponding antisymmetric combination, so it bears the same information) ; MO n°3 (or alternatively MO n°4) could be used as guess orbital for the two VB orbitals describing the 2s lone pairs of the fluorine atoms ; MO n°5 and 7 (or alternatively 6 and 8) could be used as guess for the <math>\pi_x</math> and <math>\pi_y</math> lone pairs ; last, MO n°8 describe the <math>\sigma</math> bond, and could be used as guess for the two active orbitals Then build the $gus section in XMVB input accordingly, and start your calculation (don't forget to add again vbtyp=xmvb in the $control section of Gamess input) Note that using automatic guess works fine in a simple case like this one, using guess=mo simply accelerate convergence. However, for larger molecule, specifying a good orbital guess through guess=mo and an extra $gus section will often be useful. For VBCI(D,S) calculation on difluorine : don't forget to add NCOR=2 and ctol=0.01 options in the $Ctrl section. To compute the bond energies : at the BOVB level, you can simply use the ROHF energies computed with Gamess for the separate fragments (F atoms here), because the L- and D-BOVB wave functions (like the VBSCF one) dissociate to uncorrelated separate fragments at the VBCISD level, you have to compute the separate fragments at this level of theory, and the Davidson corrected energy should be used Note that a more accurate BOVB bond energy could be obtained by pushing to higher SD-BOVB level, and with VBCISD by using a larger basis set.

Exercise 4 : The lone pairs of H₂O

(for further reading, see S. Shaik and P.C. Hiberty, "The Chemist's Guide to VB theory", Wiley, Hoboken, New Jersey, 2008, pp. 107-109)

This exercise aims at comparing two descriptions of the lone pairs of H<math>{}_2</math>O : (i) the MO description in terms of non-equivalent canonical MOs and (ii) the « rabbit-ear » VB description in terms of two equivalent hybrid orbitals.

<math>\Psi_{\textrm{MO}}</math>   <math>\Psi_{\textrm{VB}}</math>

1. Focusing on the lone pairs only, write the four-electron single-determinants <math>\Psi_{\textrm{MO}} </math> and <math>\Psi_{\textrm{VB}} </math> .
2. Expand <math>\Psi_{\textrm{VB}} </math> into elementary determinants containing only <math>n</math> and <math>p</math> orbitals, eliminate determinants having two identical spinorbitals, and show the equivalence between <math>\Psi_{\textrm{VB}}</math> and <math>\Psi_{\textrm{MO}}</math>.
3. We now remove one electron from H<math>{}_2</math>O. Write the two possible VB structures <math>\Phi_1</math> and <math>\Phi_2</math> in the VB framework. By convention, one may write the doubly occupied lone pair first, then the singly occupied one.
4. The two ionized states are the symmetry-adapted combinations 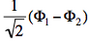and 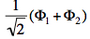. From the sign of the hamiltonian matrix element <math>\langle \Phi_1 \vert \hat{H} \vert \Phi_2 \rangle</math>, give the energy ordering of the two ionized states.
5. By expanding the two ionized states into elementary determinants (dropping the normalization constants), show that they are equivalent, respectively, to the MO configurations <math>\vert nn\bar{p}\vert</math> and <math>\vert pp\bar{n}\vert</math>.

Appendix
Hamiltonian matrix element between determinants differing by one spin-orbital : <math>\langle \cdots i \cdots \vert \hat{H} \vert \cdots j \cdots\rangle = \beta_{ij}</math> Don’t forget to put the orbitals of the two determinants in maximal correspondence before applying the rule.

Answer

1. <math> \Psi_{\textrm{MO}}=\vert n\bar{n}p\bar{p}\vert </math>   ;   <math> \Psi_{\textrm{VB}}=\vert \left( n-\lambda p\right)\left( \bar{n}-\lambda\bar{p}\right)\left( n+\lambda p\right)\left(\bar{n}+\lambda\bar{p}\right)\vert </math> 2. <math> \begin{matrix} \Psi_{\textrm{VB}} &=&\vert \left( n\bar{n} -\lambda p\bar{n} -\lambda n\bar{p} +\lambda^2 p\bar{p} \right) \left( n\bar{n} +\lambda p\bar{n} +\lambda n\bar{p} +\lambda^2 p\bar{p} \right) \vert \end{matrix} </math> <math> \begin{matrix} \Psi_{\textrm{VB}} &=&\vert n\bar{n}n\bar{n} \vert + \lambda\vert n\bar{n}p\bar{n} \vert + \lambda\vert n\bar{n}n\bar{p} \vert + \lambda^2 \vert n\bar{n}p\bar{p} \vert - \lambda \vert p\bar{n}n\bar{n} \vert -\lambda^2 \vert p\bar{n}p\bar{n} \vert -\lambda^2 \vert p\bar{n}n\bar{p} \vert -\lambda^3 \vert p\bar{n}p\bar{p} \vert \end{matrix} </math> <math> \begin{matrix} - \lambda \vert n\bar{p}n\bar{n} \vert -\lambda^2 \vert n\bar{p}p\bar{n} \vert -\lambda^2 \vert n\bar{p}n\bar{p} \vert -\lambda^3 \vert n\bar{p}p\bar{p} \vert + \lambda^2 \vert p\bar{p}n\bar{n} \vert +\lambda^3 \vert p\bar{p}p\bar{n} \vert +\lambda^3 \vert p\bar{p}n\bar{p} \vert +\lambda^4 \vert p\bar{p}p\bar{p} \vert \end{matrix} </math> After eliminating all determinants having two orbitals with the same spin, there remains : <math> \begin{matrix} \Psi_{\textrm{VB}} &=& \lambda^2 \vert n\bar{n}p\bar{p} \vert -\lambda^2 \vert p\bar{n}n\bar{p} \vert -\lambda^2 \vert n\bar{p}p\bar{n} \vert + \lambda^2 \vert p\bar{p}n\bar{n} \vert \end{matrix} </math> After permuting the columns and changing signs accordingly, there remains : <math> \Psi_{\textrm{VB}}=4\lambda^2\vert n\bar{n}p\bar{p} \vert=\Psi_{\textrm{MO}} </math> (if one includes normalization factors). 3. <math>\Phi_1=\vert \left( n-\lambda p \right)\left( \bar{n}-\lambda\bar{p} \right)\left( n+\lambda p \right) \vert </math>, <math>\Phi_2=\vert \left( n+\lambda p \right)\left( \bar{n}+\lambda\bar{p} \right)\left( n-\lambda p \right) \vert </math> Permuting the first and third orbitals in <math>\Phi_2</math> and changing the sign accordingly, we get <math>-\Phi_2</math> that has maximum orbital correspondence with <math>\Phi_1</math> : <math>-\Phi_2</math> =<math>\vert \left( n-\lambda p \right) \left( \bar{n}+\lambda\bar{p} \right) \left( n+\lambda p \right) \vert </math>. 4. <math>\Phi_1</math> and <math>-\Phi_2</math> differ by only one orbital, <math>\left( \bar{n}-\lambda \bar{p} \right)</math> in <math>\Phi_1</math> which becomes <math>\left( \bar{n}+\lambda \bar{p} \right)</math> in <math>-\Phi_2</math>. Therefore the matrix element <math> \langle \Phi_1 \vert \hat{H} \vert -\Phi_2 \rangle </math> is a simple <math>\beta</math> integral, necessarily negative. Hence, the lowest ionized state is <math> \frac{1}{\sqrt{2}}\left(\Phi_1-\Phi_2\right)</math> while the higher ionized state is <math> \frac{1}{\sqrt{2}}\left(\Phi_1+\Phi_2\right)</math>. 5. <math>\Phi_1=\vert n\bar{n}n\vert -\lambda\vert p\bar{n}n\vert -\lambda\vert n\bar{p}n\vert +\lambda^2\vert p\bar{p}n\vert+\lambda\vert n\bar{n}p\vert-\lambda^2\vert p\bar{n}p\vert-\lambda^2\vert n\bar{p}p\vert+\lambda^3\vert \bar{p}p\vert</math> <math>\Phi_1=+2\lambda^2\vert p\bar{p}n \vert +2\lambda\vert n\bar{n}p \vert</math> In the same way, one shows that <math>\Phi_2=-2\lambda^2\vert p\bar{p}n \vert +2\lambda\vert n\bar{n}p \vert</math>. It follows that : <math>\left(\Phi_1-\Phi_2\right)\propto \vert n\bar{n}p \vert </math> (lowest ionized state in MO theory) <math>\left(\Phi_1+\Phi_2\right)\propto \vert p\bar{p}n \vert </math> (higher ionized state in MO theory). It is concluded that 1) VB theory yields two ionization potentials for H<math>{}_2</math>O, in agreement with experiment, and 2) that these ionization potentials are exactly the same as the ones found in elementary MO theory.