Différences entre les versions de « VBTutorial3 »
| Ligne 6 : | Ligne 6 : | ||
== Exercise 1 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system == | == Exercise 1 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system == | ||
| − | In this exercise the <math>\textrm{S}_{\textrm{N}}2</math> reaction Cl<math>{}^{-}</math> + CH3Cl -> ClCH3 + Cl<math>{}^{-}</math> will be studied in both vacuum and solution. Valence Bond State Correlation Diagrams will be constructed at <math>\pi</math>-D-BOVB level. There are two parts in this exercise: | + | In this exercise the <math>\textrm{S}_{\textrm{N}}2</math> reaction Cl<math>{}^{-}</math> + CH3Cl -> ClCH3 + Cl<math>{}^{-}</math> will be studied in both vacuum and solution. Valence Bond State Correlation Diagrams (VBSCD) will be constructed at <math>\pi</math>-D-BOVB level. There are two parts in this exercise: basic part and optional part. The basic part is performed with MCP-DZP basis set in which the inner orbitals in Cl and C are described with MCP pseudo potential. The optional part is performed with 6-31+G* basis set, using the general specification for the xmvb input (expert users). Only reactant and transition state will be computed in this exercise, which is sufficient to build the VBSCD diagrams. <br><br> |
| − | |||
| − | <br> | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<small>'''Note:How to perform a VBPCM calculation'''</small> | ||
| + | |- | ||
| + | | | ||
| + | <small> | ||
A VBPCM calculation is performed in the similar way as the VB calculations in vacuum. One should prepare a GAMESS input file with solvent assigned such as:<br><br> | A VBPCM calculation is performed in the similar way as the VB calculations in vacuum. One should prepare a GAMESS input file with solvent assigned such as:<br><br> | ||
<center><big>$PCM SOLVNT=WATER $END</big></center><br> | <center><big>$PCM SOLVNT=WATER $END</big></center><br> | ||
The details of PCM calculation in the GAMESS can be found in GAMESS manual. Keyword "VBTYP=XMVB" in CONTRL section is also essential. After the GAMESS input file is prepared, an XMI file with keyword "VBPCM" should be prepared with the same file name as GAMESS input file. In the current XMVB package, VBSCF/PCM and BOVB/PCM calculations are both supported. | The details of PCM calculation in the GAMESS can be found in GAMESS manual. Keyword "VBTYP=XMVB" in CONTRL section is also essential. After the GAMESS input file is prepared, an XMI file with keyword "VBPCM" should be prepared with the same file name as GAMESS input file. In the current XMVB package, VBSCF/PCM and BOVB/PCM calculations are both supported. | ||
| − | < | + | </small> |
| − | + | |} | |
| − | + | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Basic part''' | ||
| + | |- | ||
| + | | | ||
'''Compute the Energies and Wavefunctions at Reactant and Transition State with Different Sets of VB Structures''' | '''Compute the Energies and Wavefunctions at Reactant and Transition State with Different Sets of VB Structures''' | ||
<br> | <br> | ||
| Ligne 45 : | Ligne 54 : | ||
# Compare the energies of reactant and product structures at reactant and transition state geometries, in both vacuum and solution. What's the difference of the energies at different points? Why? | # Compare the energies of reactant and product structures at reactant and transition state geometries, in both vacuum and solution. What's the difference of the energies at different points? Why? | ||
# Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies. | # Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies. | ||
| − | |||
| − | |||
| − | |||
| + | |} | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Optional part (expert users)''' | ||
| + | |- | ||
| + | | | ||
In this part, calculations with BFI section are performed with 6-31+G* basis set, which is desired for the experienced users. The inner orbitals are frozen as HF orbitals in all VB calculations and the valence basis functions are reorganized to hybrid basis functions so that the <math>\sigma</math>, <math>\pi_x</math> and <math>\pi_y</math> spaces can be separated well. A D-BOVB calculation is performed in 2 steps: | In this part, calculations with BFI section are performed with 6-31+G* basis set, which is desired for the experienced users. The inner orbitals are frozen as HF orbitals in all VB calculations and the valence basis functions are reorganized to hybrid basis functions so that the <math>\sigma</math>, <math>\pi_x</math> and <math>\pi_y</math> spaces can be separated well. A D-BOVB calculation is performed in 2 steps: | ||
# Perform a VBSCF calculation with <math>\pi</math> orbitals delocalized in the whole system and <math>\sigma</math> orbitals localized on the Cl and CH<math>{}_3</math> groups; | # Perform a VBSCF calculation with <math>\pi</math> orbitals delocalized in the whole system and <math>\sigma</math> orbitals localized on the Cl and CH<math>{}_3</math> groups; | ||
# Perform a BOVB calculation with VBSCF orbitals as initial guess. | # Perform a BOVB calculation with VBSCF orbitals as initial guess. | ||
The VB calculations are the same as the calculations performed above. Try to understand the BFI section, perform the calculations and compare the differences of barrier heights, resonance energies and performances with and without $BFI. | The VB calculations are the same as the calculations performed above. Try to understand the BFI section, perform the calculations and compare the differences of barrier heights, resonance energies and performances with and without $BFI. | ||
| + | |||
| + | |} | ||
[[Answer Exercise1 of tutorial 3|>> Answer]] | [[Answer Exercise1 of tutorial 3|>> Answer]] | ||
Version du 12 juillet 2012 à 11:16
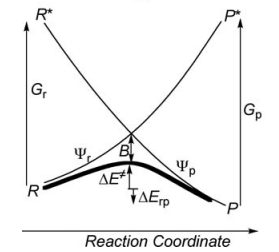
State correlation diagrams
Exercise 1 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system
In this exercise the <math>\textrm{S}_{\textrm{N}}2</math> reaction Cl<math>{}^{-}</math> + CH3Cl -> ClCH3 + Cl<math>{}^{-}</math> will be studied in both vacuum and solution. Valence Bond State Correlation Diagrams (VBSCD) will be constructed at <math>\pi</math>-D-BOVB level. There are two parts in this exercise: basic part and optional part. The basic part is performed with MCP-DZP basis set in which the inner orbitals in Cl and C are described with MCP pseudo potential. The optional part is performed with 6-31+G* basis set, using the general specification for the xmvb input (expert users). Only reactant and transition state will be computed in this exercise, which is sufficient to build the VBSCD diagrams.
| Note:How to perform a VBPCM calculation |
|---|
|
A VBPCM calculation is performed in the similar way as the VB calculations in vacuum. One should prepare a GAMESS input file with solvent assigned such as: The details of PCM calculation in the GAMESS can be found in GAMESS manual. Keyword "VBTYP=XMVB" in CONTRL section is also essential. After the GAMESS input file is prepared, an XMI file with keyword "VBPCM" should be prepared with the same file name as GAMESS input file. In the current XMVB package, VBSCF/PCM and BOVB/PCM calculations are both supported. |
| Basic part |
|---|
|
Compute the Energies and Wavefunctions at Reactant and Transition State with Different Sets of VB Structures
|
| Optional part (expert users) |
|---|
|
In this part, calculations with BFI section are performed with 6-31+G* basis set, which is desired for the experienced users. The inner orbitals are frozen as HF orbitals in all VB calculations and the valence basis functions are reorganized to hybrid basis functions so that the <math>\sigma</math>, <math>\pi_x</math> and <math>\pi_y</math> spaces can be separated well. A D-BOVB calculation is performed in 2 steps:
The VB calculations are the same as the calculations performed above. Try to understand the BFI section, perform the calculations and compare the differences of barrier heights, resonance energies and performances with and without $BFI. |
>> general guidelines for BOVB calculations