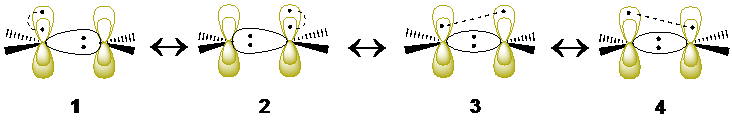Différences entre les versions de « Abstract pool hdr »
| (3 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 14 : | Ligne 14 : | ||
[1] Popelier, P. L. A.; Brémond, É. A. G. Int.J.Quant.Chem. 2009, 109, 2542. | [1] Popelier, P. L. A.; Brémond, É. A. G. Int.J.Quant.Chem. 2009, 109, 2542. | ||
| + | |||
| + | |||
| + | [http://wiki.lct.jussieu.fr/workshop/index.php/Abstract_pool_hdr ↑ top of this page] | ||
| + | |||
| + | ==Jean Philip Piquemal== | ||
| + | |||
| + | ''<big>Unraveling interactions in complex systems: from DFT to DFT/MD/Continuum simulations</big>'' | ||
| + | |||
| + | In this contribution, various applications of the NCI approach, sometime | ||
| + | coupled to other topological approaches such as QTAIM or ELF are detailed | ||
| + | in line with the global goal of the study of complex (biological systems) | ||
| + | using multi-layers QM/MM. | ||
| + | |||
| + | [http://wiki.lct.jussieu.fr/workshop/index.php/Abstract_pool_hdr ↑ top of this page] | ||
| + | |||
| + | |||
| + | ==Stéphanie Halbert, Christophe Raynaud, Christophe Copéret, Odile Eisenstein== | ||
| + | |||
| + | '''<big>Learning from calculated NMR Chemical tensors of carbon alkylidene complexes</big>''' | ||
| + | |||
| + | Combining high level calculations including relativistic corrections and NBO based analysis of the chemical shift tensors gives an interpretation of the unusual deshielding of alkylidene carbon in Schrock type d0 alkylidene transition metal complexes. These calculations also show how the chemical shifts tensors are influenced by the alpha agostic interaction, present in these complexes. | ||
| + | |||
| + | |||
| + | [http://wiki.lct.jussieu.fr/workshop/index.php/Abstract_pool_hdr ↑ top of this page] | ||
| + | |||
| + | |||
| + | ==Christophe Morell, F. Guégan, V. Tognetti, L. Joubert, H. Chermette. D. Luneau== | ||
| + | ''Université de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France'' | ||
| + | |||
| + | |||
| + | '''<big>Towards the first theoretical Scale of Trans Effect</big>''' | ||
| + | |||
| + | |||
| + | Chemical reactivity and selectivity can generally be interpreted in terms of responses of the electron energy to external perturbations. These responses constitute a set of global and local descriptors from which the chemical behavior of any electronic system can be rationalized. Within Density Functional Theory, this approach has been called conceptual DFT or Density Functional theory of chemical Reactivity [1,2]. The Dual Descriptor [3] is one of these responses. It is mathematically defined as the second derivative of the electron density with respect to the number of particles. It is also the derivative of the chemical hardness when the external potential changes. | ||
| + | |||
| + | <center>[[Image:morell.png|400px]]</center> | ||
| + | |||
| + | |||
| + | It has been shown that the sign of the DD is an indicator of the electrophilicity/nucleophilicity of an atomic site within a molecule [4,5]. This features has been extensively applied in organic chemistry [6,7] and is spreading in other fields. Very recently, new physical bases have been given to the DD [8] by expanding the electron density of a perturbed ground state through excited densities [9]. The main goal of this talk is to present these recent progresses and their applications. More precisely, part of the talk will focus on the trans effects in octahedral complexes. It will be shown that is can primarily be related to differences in the ability, for a given ligand, to cede electron density to the metal cation under the influence of the ligand on the trans position. Using the DD and its counterpart in the Grand-Canonical ensemble, a set of representative octahedral complexes have been investigated. A numerical trans-effect scale is proposed that retrieves the experimental trans orienting series [10]. | ||
| + | |||
| + | |||
| + | [1] Geerlings, P.; De Proft, F.; Langeneacker, W. Chem. Rev. 2005, 109, 205 | ||
| + | |||
| + | [2] Johnson, P.A.; Bartolotti, L.J.; Ayers, P.W.; Fievez, T.; Geerlings, P. Charge Density and Chemical Reaction: a Unified View from Conceptual DFT, in Modern Charge Density Analysis Editors: Carlo Gatti and Piero Macchi. Springer 2012 | ||
| + | |||
| + | [3] Morell, C.; Grand, A.; Toro-Labbé, A. J. Phys. Chem. A. 2005, 109, 205 | ||
| + | |||
| + | [4] Morell, C.; Grand, A.; Toro-Labbé, A. Chem. Phys. Lett. 2006, 425, 342 | ||
| + | |||
| + | [5] Morell, C.; Ayers, P.W; Grand, A.; Chermette, H. Phys. Chem. Chem. Phys, 2011, 13, 9601 | ||
| + | |||
| + | [6] Morell, C.; Grand, A.; Gutiérrez-Oliva, S.; Toro-Labbé, A. Theoretical and Computational Chemistry. Editors: Peter Politzer and Z.B. Maksic. Vol 17: Theoretical Aspects of Chemical Reactivity. Volume Editor: Alejandro Toro-Labbé. Elsevier. 2006 | ||
| + | |||
| + | [7] Geerlings, P.; Ayers, P.W; Toro-Labbé, A.; Chattaraj, P.K.; De Proft, F.; Acc. Chem. Res., 2012, 45 (5), pp 683–695 | ||
| + | |||
| + | [8] Tognetti, V.; Morell, C.; Joubert, L.; Chermette, H. Phys. Chem. Chem. Phys, 2013, 15, 14467 | ||
| + | |||
| + | [9] Guégan, F; Mignon, P.; V. Tognetti; Joubet, L.; Morell, C.; Phys. Chem. Chem. Phys. 2014, 16, 15558 – 15569 | ||
| + | |||
| + | [10] Guégan, F; Tognetti, V.; Joubert, L.; Chermette, H.; Luneau D. Morell, C.; Phys. Chem. Chem. Phys. 2015, under revision | ||
| Ligne 53 : | Ligne 113 : | ||
In the first part of the presentation, the concept of molecular switches and the different criteria of aromaticity will be briefly introduced. Then, the evolution of the aromaticity of octaphyrins subject to different external stimuli will be analyzed. Finally, the performance of the different indices will be assessed under different conditions. | In the first part of the presentation, the concept of molecular switches and the different criteria of aromaticity will be briefly introduced. Then, the evolution of the aromaticity of octaphyrins subject to different external stimuli will be analyzed. Finally, the performance of the different indices will be assessed under different conditions. | ||
| − | [[Image:twoller.jpg|700px]] | + | <center>[[Image:twoller.jpg|700px]]</center> |
Dernière version du 20 octobre 2015 à 07:52
Abstracts
Example: John Smith
University
Title
Text
[1] Popelier, P. L. A.; Brémond, É. A. G. Int.J.Quant.Chem. 2009, 109, 2542.
Jean Philip Piquemal
Unraveling interactions in complex systems: from DFT to DFT/MD/Continuum simulations
In this contribution, various applications of the NCI approach, sometime coupled to other topological approaches such as QTAIM or ELF are detailed in line with the global goal of the study of complex (biological systems) using multi-layers QM/MM.
Stéphanie Halbert, Christophe Raynaud, Christophe Copéret, Odile Eisenstein
Learning from calculated NMR Chemical tensors of carbon alkylidene complexes
Combining high level calculations including relativistic corrections and NBO based analysis of the chemical shift tensors gives an interpretation of the unusual deshielding of alkylidene carbon in Schrock type d0 alkylidene transition metal complexes. These calculations also show how the chemical shifts tensors are influenced by the alpha agostic interaction, present in these complexes.
Christophe Morell, F. Guégan, V. Tognetti, L. Joubert, H. Chermette. D. Luneau
Université de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France
Towards the first theoretical Scale of Trans Effect
Chemical reactivity and selectivity can generally be interpreted in terms of responses of the electron energy to external perturbations. These responses constitute a set of global and local descriptors from which the chemical behavior of any electronic system can be rationalized. Within Density Functional Theory, this approach has been called conceptual DFT or Density Functional theory of chemical Reactivity [1,2]. The Dual Descriptor [3] is one of these responses. It is mathematically defined as the second derivative of the electron density with respect to the number of particles. It is also the derivative of the chemical hardness when the external potential changes.
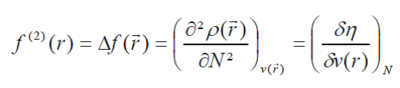
It has been shown that the sign of the DD is an indicator of the electrophilicity/nucleophilicity of an atomic site within a molecule [4,5]. This features has been extensively applied in organic chemistry [6,7] and is spreading in other fields. Very recently, new physical bases have been given to the DD [8] by expanding the electron density of a perturbed ground state through excited densities [9]. The main goal of this talk is to present these recent progresses and their applications. More precisely, part of the talk will focus on the trans effects in octahedral complexes. It will be shown that is can primarily be related to differences in the ability, for a given ligand, to cede electron density to the metal cation under the influence of the ligand on the trans position. Using the DD and its counterpart in the Grand-Canonical ensemble, a set of representative octahedral complexes have been investigated. A numerical trans-effect scale is proposed that retrieves the experimental trans orienting series [10].
[1] Geerlings, P.; De Proft, F.; Langeneacker, W. Chem. Rev. 2005, 109, 205
[2] Johnson, P.A.; Bartolotti, L.J.; Ayers, P.W.; Fievez, T.; Geerlings, P. Charge Density and Chemical Reaction: a Unified View from Conceptual DFT, in Modern Charge Density Analysis Editors: Carlo Gatti and Piero Macchi. Springer 2012
[3] Morell, C.; Grand, A.; Toro-Labbé, A. J. Phys. Chem. A. 2005, 109, 205
[4] Morell, C.; Grand, A.; Toro-Labbé, A. Chem. Phys. Lett. 2006, 425, 342
[5] Morell, C.; Ayers, P.W; Grand, A.; Chermette, H. Phys. Chem. Chem. Phys, 2011, 13, 9601
[6] Morell, C.; Grand, A.; Gutiérrez-Oliva, S.; Toro-Labbé, A. Theoretical and Computational Chemistry. Editors: Peter Politzer and Z.B. Maksic. Vol 17: Theoretical Aspects of Chemical Reactivity. Volume Editor: Alejandro Toro-Labbé. Elsevier. 2006
[7] Geerlings, P.; Ayers, P.W; Toro-Labbé, A.; Chattaraj, P.K.; De Proft, F.; Acc. Chem. Res., 2012, 45 (5), pp 683–695
[8] Tognetti, V.; Morell, C.; Joubert, L.; Chermette, H. Phys. Chem. Chem. Phys, 2013, 15, 14467
[9] Guégan, F; Mignon, P.; V. Tognetti; Joubet, L.; Morell, C.; Phys. Chem. Chem. Phys. 2014, 16, 15558 – 15569
[10] Guégan, F; Tognetti, V.; Joubert, L.; Chermette, H.; Luneau D. Morell, C.; Phys. Chem. Chem. Phys. 2015, under revision
Benoît Braïda, Andreas Savin
Université Pierre et Marie Curie
The Maximum Probability Domains method
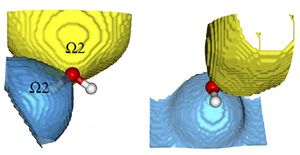
As the standard interpretation of quantum theory is probabilistic in nature, the most natural way of extracting chemical information from an accurate wave function is to consider the probability of finding specific numbers of electrons in some given regions of space.[1] The last few years, the idea to search for the regions of 3D space for which the probability of finding a given number of electrons is maximal has been investigated.[2] These regions, and the associated interpretative method, are thus called « maximum probability domains (MPDs) ». In the case of two spin-paired electrons, MPD-representations are homomorphic to Lewis structures, as they are able to give an indication of the most probable regions of space which should contain exactly two spin-paired electrons. The basics of the MPD method will be presented, and its interest illustrated through a few recent applications.
The two 2e Maximum Probability Domains associated to the valence electrons of the water molecule
[1] Savin A. (2002), In: Sen KD (ed), Reviews of modern quantum chemistry: a celebration of the 252 contributions of Robert G. Parr, World Scientific, Singapore
[2] Recent articles: (a) Mafra Lopez Jr., O. ; Braïda, B. ; Causa, M. ; Savin, A. in Progress in Theoretical Chemistry and Physics, vol 22, ed Hoggan, Springer UK, London (2011). (b) Causa, M ; Savin, A (2011) Z. Anorg. Allg. Chem. 637, 882 (c) Causa, M ; Savin, A (2011) J. Phys. Chem. A. 115, 45, 13139 (d) Causa, M ; D'Amore, M ; Garzillo, C ; Gentile, FS ; Savin, A (2013) in Applications of Density Functional Theory to Biological and Bioinorganic Chemistry, Structure and Bonding Volume 150, p119-141 (e) Menendez, M. ; Pendas, A. M. (2014) Theor. Chem. Acc. 133:1539 (f) Menendez, M. ; Pendas, A. M. ; Braïda, B.; Savin, A. (2015) Comput. Theor. Chem. 1053, 142 (g) Agostini, F. ; Ciccotti, G. ; Savin, A. (2015) J. Chem. Phys. 142, 6 (h) Causa, M ; D'Amore, M ; Gentile, F ; Menendez, M ; Calatayud, M (2015) Comput. and Theor. Chem. 1053, 315 (i) Braïda, B. ; Menendez, M. ; Pendas, A. M. ; Savin, A. manuscript in preparation.
Tatiana Woller
Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, B-1050 Brussels, Belgium.
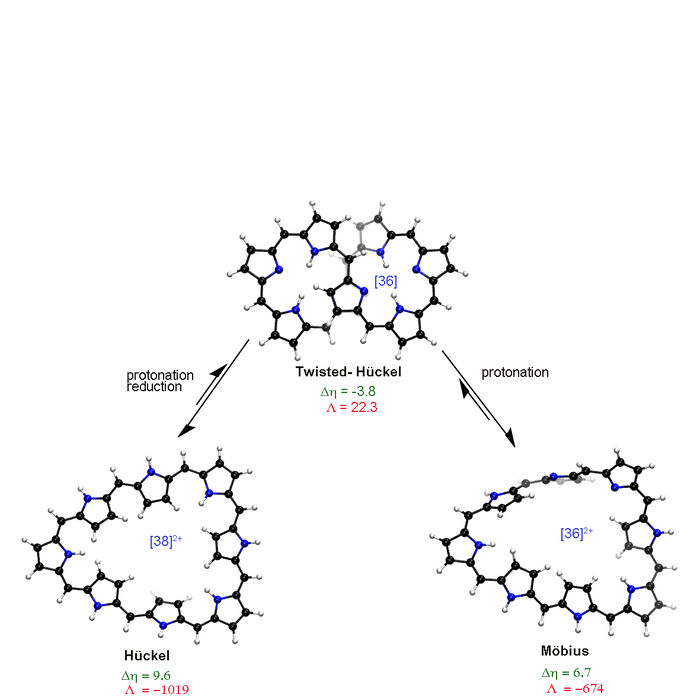
Exploring the structure-aromaticity relationship in Hückel and Möbius octaphyrins using DFT.
In the past decades, expanded porphyrins have been investigated extensively due to their interesting tunable chemical and photo-physical properties with external stimuli. As expanded porphyrins display exceptional photo-physical properties, they represent ideal candidates for the development of non-linear optical materials, near-infrared dyes or photosensitizers in biomedical applications. Among expanded porphyrins, octaphyrins, which consist of eight-pyrrolic rings, can adopt a peculiar figure-eight topology with 2 metal coordination sites and intrinsic chirality.
Several theoretical and experimental studies have pointed the existence of a close relationship between the topology, the number of π-electrons, the aromaticity and the photo-physical properties of expanded porphyrins.[1] However, the concept of aromaticity remains challenging because of its multi-dimensionality and cannot be quantified by a unique index.[2] Therefore, it is recommended to employ a set of indices based on different criteria to quantify aromaticity, as shown in several studies.[3-6]
In the first part of the presentation, the concept of molecular switches and the different criteria of aromaticity will be briefly introduced. Then, the evolution of the aromaticity of octaphyrins subject to different external stimuli will be analyzed. Finally, the performance of the different indices will be assessed under different conditions.
[1] J. M. Lim, J-Y. Shin, Y. Tanaka, S. Saito, A. Osuka and D. Kim, J. Am. Chem. Soc., 2010, 132, 3105–3114.
[2] M. K. Cyrañski, T. M. Krygowski, A. R. Katritzky, P. v. R. Schleyer, J. Org. Chem., 2002, 67, 1333–1338.
[3] M. Alonso, B. Herradón, J. Comput. Chem., 2009, 31, 917-928.
[4] M. Solà, F. Feixas, J. Oscar C. Jiménez-Halla, E. Matito ,J. Poater, Symmetry, 2010, 2, 1156-1179.
[5] F. Feixas, E. Matito, J. Poater and M. Solà, J Comput Chem, 2008, 29, 1543–1554.
[6] M. Alonso, B. Herradón, Phys. Chem. Chem. Phys., 2010, 12, 1305-1317.
Vincent Tognetti, Laurent Joubert
Normandy Univ., COBRA UMR 6014 & FR 3038, Université de Rouen, INSA Rouen, CNRS, 1 rue Tesniere 76821 Mont St Aignan, Cedex, France.
vincent.tognetti@univ-rouen.fr
The many faces of halogen bond
In this talk, I will review part of our recent works dealing with halogen bonds[1] (ubiquitous in biology and material science), with a particular emphasis on interpretative tools based on the electron density.
In particular, conceptual DFT[2] will be invoked to characterize the electrophilicity of the halogen atoms through the usual or state-specific dual descriptors[3] and their partition in real space into reactive domains.[4] This arsenal will be shown to afford an explanation for the bond formation that is complementary to the pure electrostatic one embodied in the so-called σ-hole paradigm,[5] paradigm that we also recently revisited.[6]
In addition, the interactions at work once the complex is formed (while conceptual DFT focuses on the intrinsic properties of the fragments before they interact) will be analyzed in details using Pendás’ interacting quantum atoms scheme[7] within Bader’s atoms-in-molecules theory.[8] The role of secondary interactions, of covalency and dispersion will be particularly scrutinized, as well in intermolecular[9,10] as in intramolecular halogen bonds.[11-13]
[1] P. Metrangolo, G. Resnati, Cryst. Growth Des. 2012, 12, 5835
[2] P. Geerlings, F. De Proft, W. Lengenaeker, Chem. Rev. 2003, 103, 1793
[3] V. Tognetti, C. Morell, P.W. Ayers, L. Joubert, H. Chermette, Phys. Chem. Chem. Phys. 2013, 15, 14465
[4] V. Tognetti, C. Morell, L. Joubert, J. Comput. Chem. 2015, 36, 649
[5] P. Politzer, J.S. Murray, T. Clark, Phys. Chem. Chem. Phys. 2013, 15, 11178
[6] V. Tognetti, L. Joubert, Theor. Chem. Acc. 2015, 134, 90
[7] M.A. Blanco, A.M. Pendás, E. Francisco, J. Chem. Theory Comput. 2004, 1, 1096
[8] R.F.W. Bader, Atoms in Molecules: A Quantum Theory; Oxford University Press, New York, 1990
[9] O.A. Syzgantseva, V. Tognetti, L. Joubert, J. Phys. Chem. A 2013, 117, 8969
[10] V. Tognetti, L. Joubert, Challenges and Advances in Computational Chemistry and Physics, in press
[11] V. Tognetti, L. Joubert, J. Chem. Phys. 2013, 138, 024102
[12] M. Yahia-Ouahmed, V. Tognetti, L. Joubert, Comput. Theor. Chem. 2015, 1053, 254
[13] M. Yahia-Ouahmed, V. Tognetti, L. Joubert, in preparation
Dennis R. Salahub
University of Calgary, Department of Chemistry, Centre for Molecular Simulation, Institute for Quantum Science and Technology, Institute for Sustainable Energy, Environment and Economy, 2500 University Drive NW, Calgary, AB, Canada T2N 1N4
dennis.salahub@ucalgary.ca, xingliu@ucalgary.ca
Molybdenum carbide nanoparticles as catalysts for hydrogenation reactions, between clusters and the bulk
A gap exists in understanding heterogeneous catalysis between a cluster of a few atoms and a periodic slab model; reactions catalyzed by transition-metal-containing nanoparticles are still not well understood. In this presentation, we provide a multiscale modelling approach to study benzene hydrogenation on molybdenum carbide nanoparticles (MCNPs) in the process of in-situ heavy oil
upgrading. The QM DFTB method is coupled with an MM force field to yield a quantum mechanical/molecular mechanical (QM/MM) model describing the reactants, the nanoparticles and the surroundings. Umbrella sampling (US) was employed to calculate the free energy profiles for benzene hydrogenation in a model aromatic solvent under realistic conditions. Comparisons are made with the traditional methodologies; the results reveal new features of the metallic MCNPs. Under working conditions, rather than being rigid, they are very flexible due to the entropic contributions of the MCNPs and the solvent, which greatly affect the free energy profiles.
Mohamed Amaouch,a Julien Pilmé, a Nicolas Gallandb
aLaboratoire de Chimie Théorique Université Pierre et Marie Curie and CNRS. F-75005, Paris, France
bLaboratoire CEISAM, Université de Nantes, Nantes, France
The ELF and AIM topological analyses in the context of the quasirelativistic approach
There is currently a growing interest in using relativistic methods as it has become clear that the study of chemistry involving elements across the entire periodic table requires that relativistic effects are taken into account. The most rigorous approaches are based on the four-component (4c) formalism (Dirac equation) but several alternative two- component (2c) methods were proposed. The 2c methods are notably able to account for spin-orbit (SO) effects. However, the study of SO effects inside the chemical bond appears hindered mainly by the exclusive use of molecular orbital (MO) theory and the related Mulliken populations. Alternative strategies can be proposed to analyze the breaking and the formation of bonds between atoms : atoms in molecules theory (AIM) which relies on the properties (topology) of the total electron density when atoms interact or the Electron Localization Function (ELF) which is a signature of the electronic pairs distribution [1, 2, 3].In this context, an original formulation of ELF and AIM descriptors and their topologies were extended to the framework of 2c quantum calculations [4]. Illustrations of the SOC effects on the bond representation will be given for selected astatine (At, Z=85) species.
[1] Axel D Becke and Kenneth E Edgecombe. The Journal of chemical physics, 92(9) :5397-5403, 1990.
[2] Bernard Silvi and Andreas Savin. Nature, 371(6499) :683–686, 1994.
[3] Richard FW Bader. Atoms in molecules, 1990.
[4] Julien Pilmé, Eric Renault, Tahra Ayed, Gilles Montavon, and Nicolas Galland. Journal of Chemical Theory and Computation, 8(9) :2985–2990, 2012.
Roberto A. Boto
1. Sorbonne Universités. Université Pierre et Marie Curie. Institut du Calcul et de la Simulation. 75005. Paris. France.
2. Laboratoire de Chimie Théorique Université Pierre et Marie Curie and CNRS. F-75005, Paris. France.
On the interpretation of the reduced density gradient
Non-covalent interactions (NCIs) play a key role in many areas of science, ranging from biochemistry to condensed matter. In this regard, the NCI index has been proposed as a new tool to identify and characterise weak interactions of various strengths as chemical intuitive reduced density gradient (RDG) isosurfaces, that reveal both stabilising(hydrogen bonding and van der Waals interactions) and destabilising interactions.[1] Beyond qualitative analysis, the integration of both volume and charge within NCI isosurfaces are in good agreement with the hydrogen-bonding potential-energy surfaces. [2] Recently Saleh et al. found a good linear correlation between stabilisation energies and kinetic energies integrated on the main NCI isosurfaces. [3] These results connect the topology of RDG with energetics. In the present work we analyse the origin of these correlations through a set of molecular systems representing covalent, ionic and non-covalent interactions. A chemically sound interpretation of RDG is also presented.
[1] R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen, and W. Yang, “Revealing Noncovalent Interactions”, J. Am. Chem. Soc. 132 , 6498 (2010)
[2] J. Contreras-Garcia, E. R. Johnson, W. Yang, “Analysis of Hydrogen-Bond Interaction Potentials from the Electron Density: Integration of Noncovalent Interaction Regions”, J. Phys. Chem. A 115, 12983 (2011)
[3] G. Saleh, C. Gatti, L. L. Presti, “Energetics of non-covalent interactions from electron energy density distributions”. Comp. Theo. Chem., 1053, 53 (2015)
Frank de Proft
Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, B-1050 Brussels, Belgium.
Density Functional Theory Reactivity Indices: Theoretical Developments,
Application in Transition Metal Chemistry and Inverse Design of Molecules with
Optimal Reactivity Properties
Conceptual Density Functional Theory (sometimes also called DFT based reactivity theory or Chemical DFT) has proven to be an ideal framework for the introduction of chemical reactivity descriptors. These indices are defined as response functions of the energy E of the system with respect to either the number of electrons N, the external potential ν(r) or both. These definitions have afforded their non- empirical calculation and applications in many fields of chemistry have been performed.
In a first part of the talk, attention will be focused on the so-called linear response function (or polarizability kernel) defined as the second derivative of the energy with respect to the external potential. We will give an overview of the chemistry that can be extracted from this quantity: the kernel is shown to provide a measure of electron delocalization and a connection is made to the concept of aromaticity.
In a second part, an investigation will be presented of structural and electronic requirements of ligand non-innocent behavior in transition metal complexes.
Finally, we will highlight an application of the so-called inverse design methodology, using the reactivity indices to design molecules with optimal reactivity properties. More specifically, this approach will be used to construct radicals with unprecedented stabilities. The design of molecules with optimal properties is an important challenge in chemistry because of the astronomically large number of possible stable structures that are accessible in chemical space. The thiadiazinyl radical was chosen as case study of this new approach, and the optimized property of this compound was the intrinsic radical stability. The resulting optimal structure was found to be highly stable, intrinsically more so than other well-known stable radicals.
Henry Chermette,a Walid Lamine,a,b Christophe Morella
a Université de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France
b Université de Tunis El Manar, Faculté des Sciences de Tunis, UR11ES19 Unité de recherche Physico-Chimie des Matériaux condensés, El-Manar II, 2092, Tunis, Tunisie
Ill-advised self-interaction contribution in modeling anionic attack in a reaction path.
The catalytic role of an anion such as iodide in the insertion of CO2 into an epoxide over a Zn complex is presented.
It is shown how the contribution of the iodide ion may be incorrectly modeled in a reaction path, and how the ill-advised self-interaction contribution may be approximately cured.
Philippe C. Hiberty, Wei Wu, Huaiyu Zhang, Benoît Braida, Sason Shaik
V state of ethylene: from myriads of MO-CI configurations to just four valence bond structures
The first singlet excited state of ethylene (so-called the V state) is a notoriously difficult test case that has necessitated elaborate strategies and extensive configuration interaction in the molecular orbital (MO) framework. By contrast, the description of this electronic state and its transition energy from the ground state (so-called the N state), becomes very simple with valence bond methods. It is shown that extremely compact wave functions, made of three VB structures for the N state and four structures for the V state (1-4 in the scheme below), provide an N→V transition energy of 8.01 eV, in good agreement with experiment (7.88 eV for the N→V transition energy estimated from experiments). Further improvement to 7.96/7.93 eV is achieved at the variational and diffusion Monte Carlo (MC) levels, using a Jastrow factor coupled with the same compact VB wave functions. Furthermore, the measure of the spatial extension of the V state wave function, 19.14 a02, is in the range of accepted values obtained by large-scale state-of-the-art MO-based methods. The σ response to the fluctuations of the π electrons in the V state, known to be a crucial feature of the V state, is taken into account using the breathing-orbital valence bond method (BOVB), which allows the VB structures to have different sets of orbitals, as is made apparent in 1 and 2. Further valence bond calculations in a larger space of configurations confirm the results of the minimal structure-set, yielding an N→V transition energy of 7.97 eV and a spatial extension of 19.16 a02 for the V state. Both types of valence bond calculations show that the V state of ethylene is not fully ionic as usually assumed, but involving also a symmetry-adapted combination of VB structures,3 and 4, each with asymmetric covalent π bonds. The latter VB structures have cumulated weights of at least 18-26%, and stabilize the V state by about 0.9 eV. It is further shown that these latter VB structures, rather than the commonly considered zwitterionic ones, are the ones responsible for the spatial extension of the V state, known to be ca. 50% larger than the V state.
Aurélien de la Lande
Laboratoire de Chimie Physique, Université Paris Sud, CNRS, Université Paris Saclay. 15, avenue Jean Perrin, 91405 Orsay, Cedex. France
Robust, basis-set independent method for the evaluation of charge-transfer energy in nonconvalent complexes
Separation of the energetic contribution of charge transfer to interaction energy in noncovalent complexes would provide important insight into the mechanisms of the interaction. However, the calculation of charge-transfer energy is not an easy task. It is not a physically well-defined term and the results might depend on how it is described in practice. Commonly, the charge transfer is defined in terms of molecular orbitals; in this framework, however, the charge transfer vanishes as the basis set size increases towards the complete basis set limit. This can be avoided by defining the charge transfer in terms of the spatial extent of the electron densities of the interacting molecules, but the schemes used so far do not reflect the actual electronic structure of each particular system and thus are not reliable. We propose a novel approach – spatial partitioning of the system which is based on a charge transfer-free reference state, namely superimposition of electron densities of the non-interacting fragments. We show that this method, employing constrained DFT for the calculation of the charge-transfer energy, yields reliable results and is robust with respect to the strength of the charge transfer, the basis set size and the DFT functional used. Because it is based on DFT, the method is applicable to rather large systems.
[1] Řezáč, J; de la Lande, A. J. Chem. Theor. Comput. 2015, 11, 528-537.
A. Martín Pendás
Universidad de Oviedo, Julian Claveria, 33006, Oviedo, Spain
Electron distribution functions from academic models: towards a real space Aufbau principle
Electron number distribution functions (EDFs) allow for the computation of the weights of
real space resonance structures. To obtain them we need a partition of
space into chemically meaningul regions, i.e. through QTAIM, ELF, Hirshfeld, or any other
exhaustive or fuzzy decomposition available in the literature.
With such a decomposition we may compute the probability of distributing the N electrons of a molecular system into the m regions in which we have divided space, in every possible way. EDFs provide valuable insight into chemical bonding, and here we show that they may be successfully approximated by very simple models, giving rise to an interesting interpretation of the standard Aufbau principle in real space. This is obtained from academic models of the wave functions of simple systems and a Mulliken-like condensation.
P. Reinhardt, P. Chaquin
LCT, UPMC, Paris, France
Realistic molecular frequencies from a simple atomic-density model
Based on the Hellmann-Feynman theorem we construct a simple model for calculating force constants in molecular, poly-nuclear frameworks. We show the vibrational frequencies for homonuclear diatomics are obtained with an astonishing precision, and for larger molecules domains of frequencies can be identified.