Différences entre les versions de « VBTutorial4 »
| (233 versions intermédiaires par 4 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | [[ | + | [[VB_tutorial|<<< VB tutorials main page]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =BLW method & HuLiS program= | |
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big>'''BLW within GAMESS (Version: MAR-25-2010 R2)'''</big> | ||
| + | |- | ||
| + | | | ||
| + | [[BLW | BLW ]] is provided by [http://homepages.wmich.edu/~ymo/ Yirong Mo] (Western Michigan University - USA). It allows to optimize local wave functions. DFT approaches allow to include a part of correlation into the structure. | ||
| + | Gradients are available for geometry optimization. Structures can interact with $BLWCI group. | ||
| + | During the workshop, a BLW computation of file.inp is obtained with the command "blwrun file " | ||
| + | file.log and file.blw are in the current directory. | ||
| − | + | [[BLW | BLW help]] | |
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | {| class="collapsible collapsed wikitable" | |
| + | |- | ||
| + | !<big>'''HuLiS : a Huckel-based code'''</big> | ||
| + | |- | ||
| + | | | ||
| + | [[File:hulis.png|thumb|right| 100px|alt=Huckel - Lewis alt text | Huckel - Lewis]] | ||
| − | + | HuLiS is provided by [http://www.ism2.univ-cezanne.fr/equipes/CTOM_1.htm Stephane Humbel ] (Aix-Marseille Université - France). | |
| − | |||
| − | + | This is a graphical java applet that deals with Huckel and Lewis structures. It computes coefficients and weights of mesomeric structures through two different approaches: the energy related approach is a simulated CI (HL-CI - deprecated); the wave function approach is a projection of Lewis structures onto a Huckel derived wave function(HLP). This second approach is more reliable. | |
| − | + | HuLiS is launch with the command "java -jar ~/bin/hulis.jar" or via the web site [http://www.hulis.free.fr/ HuLiS ] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Details of the principles are written at | |
| − | + | [http://www.hulis.free.fr/huckel_theory_delocalization/index.shtml HL-CI and HLP explanations]. | |
| − | + | Seminal papers are [http://wiki.lct.jussieu.fr/workshop/images/4/43/HL-CI-JCEp1056.pdf HL-CI] and [http://wiki.lct.jussieu.fr/workshop/images/d/d3/HLP2008.pdf HLP]. | |
| − | + | |} | |
| − | |||
| − | |||
| − | = | + | {| class="collapsible collapsed wikitable" |
| − | + | |- | |
| + | !<big><big><big>'''Main exercises'''</big></big></big> | ||
| + | |- | ||
| + | | | ||
| + | == Exercice 1 (Lewis structures of benzene, resonance) == | ||
| − | + | {| class="collapsible collapsed wikitable" | |
| − | + | |- | |
| − | + | !<big>'''Topic'''</big> | |
| − | + | |- | |
| − | + | | | |
| − | + | The benzene molecule is commonly represented as the resonance between the two Kékulé structures. The aim of the exercise is to understand the relative importance of the different Lewis structures in the benzene molecule using BLW and [http://www.hulis.free.fr/ HuLis]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | According to IUPAC’s Goldbook, resonance energy is defined as “The difference in potential energy between the actual molecular entity and the contributing structure of lowest potential energy”. However this definition does not precise what is the geometry of the contributing structure of lowest potential energy. Consequently, we can define two types of resonance energy: the vertical resonance energy (VRE) and the adiabatic resonance energy (ARE). This exercice tutorial will guide us toward Lewis structures and resonance of benzene. | |
| + | |} | ||
| − | + | The 6-31G(d) basis set will be used in the following. | |
| − | |||
| − | |||
| − | + | 1/ Vertical Resonance Energy - at the geometry of benzene. | |
| − | + | With the BLW program, and using the provided optimized geometry of benzene molecule, define one 1,3,5-cyclohexadiene Lewis structure, and optimize it's orbitals. 4 blocks need to be defined : 3 blocks for 3 pi bond, and 1 for all the sigma electrons. | |
| − | + | Using benzene energy, calculate the Vertical Resonance Energy (VRE). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 2/ Adiabatic Resonance Energy (ARE)- relax the Lewis structure geometry | ||
| − | + | With the BLW program, relax the Lewis' structure geometry. | |
| − | |||
| − | |||
| − | |||
: Compare the C-C bond distances to benzene's. Ensure that it is consistent with the Lewis structure. | : Compare the C-C bond distances to benzene's. Ensure that it is consistent with the Lewis structure. | ||
: Compute the Adiabatic Resonance Energy (ARE) and comment. | : Compute the Adiabatic Resonance Energy (ARE) and comment. | ||
| − | : Compare the resonance energies computed by the BLW method to the conventional experimental resonance energy based on the hydrogenation heats of benzene and cyclohexene. | + | : Compare the resonance energies computed by the BLW method to the conventional experimental resonance energy based on the hydrogenation heats of benzene and cyclohexene (36 kcal/mol). |
| − | 3 | + | |
| + | 3/ With HuLiS, evaluate the space spanned by Lewis structures compared to that of delocalized wave functions. | ||
: Draw the benzene with the Huckel tools (blue, left) and create two Kekules structures with the Lewis tools. Double bonds are obtained by clicking a single bond - A second click returns to the Single bond. | : Draw the benzene with the Huckel tools (blue, left) and create two Kekules structures with the Lewis tools. Double bonds are obtained by clicking a single bond - A second click returns to the Single bond. | ||
| Ligne 102 : | Ligne 81 : | ||
: Add to the wave function the 3 covalent Dewar structures. | : Add to the wave function the 3 covalent Dewar structures. | ||
::How does <math>{\tau}</math> vary? | ::How does <math>{\tau}</math> vary? | ||
| − | : Remove all structures [Erase Mesomery] and automatically generate all possible structures having one charge separation | + | : Remove all structures [Erase Mesomery] and automatically generate all possible structures having one charge separation: |
| + | ::<mode><expert mode> [Generate all] | ||
| + | ::Note the value of <math>{\tau}</math>, and the weight of all Lewis structures needed ([Results]). | ||
| − | + | [[VBFile 4-1 | FILES FOR BENZENE]] | |
| − | [[VBFile 4-1 | | ||
| + | == Exercice 2 (allyl) == | ||
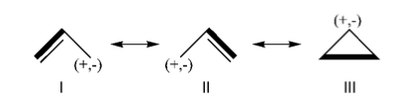
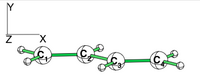
| + | [[File:Allyl.png|400px|thumb|right]] | ||
| − | + | *1/ With the BLW code calculate the relative energies of the three Lewis structures of the allyl cation at the HF level. By comparison with the energy of the allyl cation, determine the VRE and the ARE. Compare the C-C bond distances. | |
| − | + | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Hints''' | ||
| + | |- | ||
| + | | | ||
| + | * Starting from the delocalized geometry, the first iteration of the optimization of the localized structure will give the VRE. | ||
| + | |} | ||
| + | |||
| + | *2/ Repeat the first question at the B3LYP level. | ||
| + | |||
| + | *3/ Repeat questions 1 and 2 for the allyl radical. | ||
| + | [[VBFile 4-2 | FILES FOR THE ALLYLS]] | ||
| − | == | + | == Exercise 3 (BH3... NH3) electronics at the B3LYP 6-31G(d) level == |
| − | |||
| − | |||
BLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps. | BLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps. | ||
| − | + | {| class="collapsible collapsed wikitable" | |
| + | |- | ||
| + | !<big>'''Geometry'''</big> | ||
| + | |- | ||
| + | | | ||
| + | the geometry of the complex we use is | ||
<html><pre> | <html><pre> | ||
$DATA | $DATA | ||
| Ligne 133 : | Ligne 130 : | ||
$END | $END | ||
</pre></html> | </pre></html> | ||
| − | + | |} | |
| − | + | *1/ Make orbitals of BH3 alone (then NH3) in the geometry of the complex | |
| − | '''Preliminary Remarks :''' | + | *2/ Let fragment orbitals to polarize in the full complex. |
| + | |||
| + | *3/ Let delocalize. This is just a standard DFT calculation. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big>'''Preliminary Remarks :'''</big> | ||
| + | |- | ||
| + | | | ||
B3LYP calculation in Gamess is specified in $CONTRL : | B3LYP calculation in Gamess is specified in $CONTRL : | ||
<pre> $CONTRL SCFTYP=RHF DFTTYP=B3LYP runtyp=energy maxit=200 icharg=0 $END</pre> | <pre> $CONTRL SCFTYP=RHF DFTTYP=B3LYP runtyp=energy maxit=200 icharg=0 $END</pre> | ||
| Ligne 143 : | Ligne 148 : | ||
<pre> $BASIS GBASIS=N31 NGAUSS=6 NDFUNC=1 $END</pre> | <pre> $BASIS GBASIS=N31 NGAUSS=6 NDFUNC=1 $END</pre> | ||
| − | + | |} | |
| − | 1/ Perform a NH3 BLW calculation of the fragment alone in the geometry of the | + | {| class="collapsible collapsed wikitable" |
| + | |- | ||
| + | !<big>'''Step by step help :'''</big> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | *1/ Perform a NH3 BLW calculation of the fragment alone in the geometry of the complex with '''$BLW NBLOCK=1 $END''' and keep the generated .blw file for next step (same for BH3). | ||
<font color=grey> | <font color=grey> | ||
| − | We obtain | + | :: We obtain |
| − | + | :: nh3.log: FINAL R-B3LYP ENERGY IS -56.5111505350 | |
| − | nh3.log: FINAL R-B3LYP ENERGY IS -56.5111505350 | + | :: bh3.log: FINAL R-B3LYP ENERGY IS -26.5644674370 |
| − | |||
| − | bh3.log: FINAL R-B3LYP ENERGY IS -26.5644674370 | ||
| − | |||
= > summ = -83.07561797</font> | = > summ = -83.07561797</font> | ||
| − | 2/ Do the complex in a NBLOCK=2 BLW calculation and see the polarization of each fragment. | + | *2/ Do the complex in a NBLOCK=2 BLW calculation and see the energetic effect of the polarization of each fragment. The initial orbitals are obtained from .blw files of individual fragments |
| − | The initial orbitals are obtained from .blw files of individual fragments | ||
---ORBITALS (LOCAL BFS)--- part, and copied after the $BLWDAT fragments definition. A blank line separate each fragments’guess. | ---ORBITALS (LOCAL BFS)--- part, and copied after the $BLWDAT fragments definition. A blank line separate each fragments’guess. | ||
| Ligne 164 : | Ligne 171 : | ||
<font color=grey> | <font color=grey> | ||
| − | We obtain | + | ::We obtain |
| + | ::ITER 1 E(RBLW) = -83.059219 </font> | ||
| + | ::<font color=grey>FINAL R-B3LYP ENERGY IS -83.093218</font> compared to the 1st iteration it is -21.3 kcal/mol= electronic relaxation | ||
| + | |||
| + | *3/ Let the delocalization of all electrons. (NBLOCK=1 + read localized guess orbitals OR standard B3LYP calculation) | ||
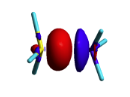
| + | [[File:EDD_map.png|right| 200px|alt=EDD map - EDD alt text | differential density]] | ||
| + | <font color=grey> | ||
| + | ::We obtain | ||
| + | ::FINAL R-B3LYP ENERGY IS -83.148013 </font> -34.4 kcal/mol charge transfer. | ||
| + | '''Remark0''' : BSSE can be computed with CP approach and use to correct this energy. A ghost atom is noted with a negative Z (e.g. a ghost Carbone in noted as C -6.0 X Y Z instead of C 6.0 X Y Z). | ||
| + | |||
| + | '''Remark''' : the electronic differential density can be mapped using BLW and DELOCALIZED cube files generate with gaussian for instance. An utility ('''edd''') substracts the two densities from the cube files named '''test.cube_BLW''' and '''test.cube_HF''' and stores it in the file '''test.cub'''. The new cube file can be visualized with gaussview ('''gview'''). | ||
| + | |||
| + | |||
| + | to generate the cube file for BLW orbitals, use Gaussian ('''gaurun''') with this route card | ||
| + | #B3LYP/6-31G(d) 6D Nosymm Guess=(Cards,'''only''') Cube=(81,Density,Full) | ||
| + | |||
| + | and after the geometry specification, | ||
| + | input the orbitals from the BLW file as cards, | ||
| + | don't forget to name the cube file. | ||
| + | '''test.cube_BLW''' | ||
| + | see also [[VBFile_4-3#gaussiancube.com | gaussiancube file]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | [[VBFile 4-3 | FILES FOR THE NH3 ... BH3]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big><big><big>'''Optional exercises - homework'''</big></big></big> | ||
| + | |- | ||
| + | | | ||
| + | |||
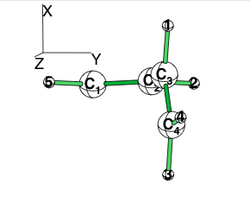
| + | == Exercise 4 (Butadiene deconjugation without hyperconjugation) == | ||
| + | [[File:Rotated_butadiene.png|right|150px|alt=butadiene - Lewis alt text | planar butadiene ]] | ||
| + | [[File:planar_butadiene.png|right|200px|alt=butadiene - Lewis alt text | planar butadiene ]] | ||
| + | Examine the conjugation in planar butadiene and the hyperconjugation in perpendicular butadiene, and explain the rotational barrier. | ||
| + | |||
| + | Note that often people rotate one participating group to disable the conjugation and use the barrier to measure the conjugation energy. What is the inconvenience of this approach? | ||
| + | |||
| + | |||
| + | * Compute the conjugated planar form with a standard B3LYP/6-31G(d) calculation | ||
| + | * Using BLW, localize the pi electrons on C1=C2 and on C3=C4 double bonds. (view the geometrie to verify that the pi system is along the X axis. | ||
| + | * Compare the energies to calculate the conjugaison energy. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Planar geometry''' | ||
| + | |- | ||
| + | | | ||
| + | <html><pre> | ||
| + | C 6.0 0.0000000000 0.6097325637 1.7490045499 | ||
| + | C 6.0 0.0000000000 0.6038280097 0.4085967284 | ||
| + | C 6.0 0.0000000000 -0.6038307169 -0.4085950903 | ||
| + | C 6.0 0.0000000000 -0.6097309803 -1.7490029472 | ||
| + | H 1.0 0.0000000000 1.5343833559 2.3190652626 | ||
| + | H 1.0 0.0000000000 -0.3149186339 2.3230080652 | ||
| + | H 1.0 0.0000000000 1.5514513284 -0.1322302753 | ||
| + | H 1.0 0.0000000000 -1.5514569088 0.1322266423 | ||
| + | H 1.0 0.0000000000 -1.5343794820 -2.3190677945 | ||
| + | H 1.0 0.0000000000 0.3149214640 -2.3230051413 | ||
| + | </pre></html> | ||
| + | |} | ||
| + | * Use the perpendicular form given below to compute the "deconjugated" system. The comparairison with the planar standard calculation gives an estimate of the conjugaison, which is contaminated by some hyperconjugaison. | ||
| + | * To inhibit hyperconjugaison in the perpendicular form, localize the electrons on the C1=C2 and on C3=C4 double bond. (note that the C3=C4 vinyl group has rotated along the XZ plane; hence its pi system is along the Y axis. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Twisted (perpendicular) geometry''' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | <html><pre> | ||
| + | C 6.0 0.000000 -1.086858 2.236154 | ||
| + | C 6.0 0.000000 0.000000 1.489418 | ||
| + | C 6.0 0.000000 0.000000 0.000000 | ||
| + | C 6.0 -1.086858 0.000000 -0.746736 | ||
| + | H 1.0 0.967527 0.000000 -0.478451 | ||
| + | H 1.0 0.000000 0.967527 1.967869 | ||
| + | H 1.0 -2.072275 0.000000 -0.314213 | ||
| + | H 1.0 -1.029400 0.000000 -1.820913 | ||
| + | H 1.0 0.000000 -2.072275 1.803631 | ||
| + | H 1.0 0.000000 -1.029400 3.310331 | ||
| + | $END | ||
| + | |||
| + | </pre></html> | ||
| + | [[File:Rotated_butadiene.png|right|250px|alt=butadiene - Lewis alt text | planar butadiene The C3=C4 has rotated along the XZ plane; hence its pi system is along the Y axis.]] | ||
| + | |||
| + | |} | ||
| + | [[VBFile 4-4 | FILES FOR THE BUTADIENE DECONJUGAISON ]] | ||
| + | |||
| + | == Exercise 5 : formamide and allyl radical with HuLiS == | ||
| + | |||
| + | Here are two HuLiS exercices : find the weights in formamide with HL-CI and use HLP to get coefficients for the allyl radical. | ||
| + | |||
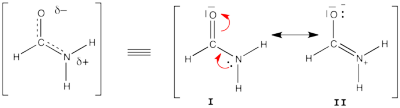
| + | ====Formamide with HL-CI==== | ||
| + | [[File:Formamide.png|400px|thumb|right]] | ||
| + | Formamide can be written as a resonance between two Lewis strutures. We shall find the weights of this scheme using HL-CI. | ||
| + | |||
| + | In HL-CI we define an effective CI hamiltonian that concerns the interaction between the (localized) Lewis structures <math> \Psi_{I}</math> and <math> \Psi_{II}</math>: <math> \Psi_{HL-CI}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. This CI must give the Huckel energy of the delocalized wave function. <math> E_{HL-CI}=E_{Huckel}</math> | ||
| + | |||
| + | *1/ Write the expression of the CI secular determinant that has the energy ot the delocalized wave function, and show that the off-diagonal term is <math>H_{I-II}=0.71\beta</math>. (in HL-CI the off diagonal term is supposed <0). | ||
| + | |||
| + | *2/ Resolve the secular equations of the CI and find that | ||
| + | <math> \Psi_{HL-CI}=0.81\Psi_{I}+0.58\Psi_{II}</math>, hence the weights of the structures (I/II)=(66%/34%) | ||
| + | |||
| + | Note that in HL-CI <math><\Psi_{I}|\Psi_{II}>=0</math> | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''help''' | ||
| + | |- | ||
| + | | | ||
| + | Formamide's Huckel energy <math>E_{Huckel}= 4\alpha + 6.548\beta</math> | ||
| − | + | The (localized) Lewis structures '''I''' and '''II''' have an energy of | |
| + | ** <math>E_{I}= 2*(\alpha + 1.370\beta)+2*(\alpha+1.651\beta)= 4\alpha + 6.041\beta</math> | ||
| + | ** <math>E_{II}= 2*(\alpha + 1.808\beta)+2*(\alpha+0.970\beta)= 4\alpha + 5.556\beta</math> | ||
| − | + | These values are used as <math>H_{I-I}</math> and <math>H_{II-II}</math> for the CI matrix. | |
| + | |} | ||
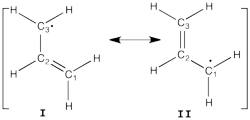
| − | + | ====Allyl Radical with HLP==== | |
| + | [[File:Allyl_radical.png|250px|thumb|right]] | ||
| + | Allyl radical can be written as a resonance between two Lewis strutures: <math> \Psi_{HLP}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. | ||
| + | We shall find the coefficients of this CI via HLP. The Huckel orbitals are considered as : | ||
| − | < | + | ** <math> \phi_1=0.5 p_1 + 0.7 p_2 + 0.5 p_3 </math> |
| + | ** <math> \phi_2=0.7 p_1 + 0.0 p_2 - 0.7 p_3 </math> | ||
| + | ** <math> \phi_3=0.5 p_1 - 0.7 p_2 + 0.5 p_3 </math> | ||
| + | In the following the Huckel wave function is expressed as a Salter determinant: <math> \Psi_{Huckel}=|\phi_{1}\bar{\phi_{1}}\phi_2|</math> | ||
| + | In the HLP scheme we search the coefficient of the structures I and II by projection of the Huckel wave function onto the localized structures <math> \Psi_{I}=|\pi_{12}\bar{\pi_{12}}p_3|</math> and <math>\Psi_{II}=|p_1\pi_{23}\bar{\pi_{23}}|</math>. | ||
| + | ======Overlap between Lewis structures ====== | ||
| + | Within Huckel approximation, (<math> <p_{i}|p_{j}>=\delta_{ij}</math>) | ||
| + | *1/ Find that <math> <\Psi_{I}|\Psi_{II}>=-0.25</math>. | ||
| + | *2/ Suppose that <math> <\Psi_{I}|\Psi_{Huckel}>=-0.73</math> and <math><\Psi_{II}|\Psi_{Huckel}>=+0.73</math>. | ||
| + | Find <math>c_I</math> and <math>c_{II}</math> by solving the equations that derive from | ||
| + | **<math><\Psi_I|\Psi_{Huckel}>=<\Psi_I|\Psi_{HLP}></math> | ||
| + | **<math><\Psi_{II}|\Psi_{Huckel}>=<\Psi_{II}|\Psi_{HLP}></math> | ||
| + | *3/ Compute the trust factor <math>\tau=<\Psi_{HLP}|\Psi_{huckel}></math> | ||
| − | + | *4/ Remark: HL-CI fails to give the correct signs because it supposes <math>H_{I-II}<0</math>. | |
| − | </ | + | This drawback can be shown using the energies of the occupied Huckel orbitals <math> \epsilon_1=\alpha+1.41\beta</math> and<math> \epsilon_2=\alpha</math> |
| − | + | |} | |
Dernière version du 14 février 2013 à 08:27
BLW method & HuLiS program
| BLW within GAMESS (Version: MAR-25-2010 R2) |
|---|
|
BLW is provided by Yirong Mo (Western Michigan University - USA). It allows to optimize local wave functions. DFT approaches allow to include a part of correlation into the structure. Gradients are available for geometry optimization. Structures can interact with $BLWCI group. During the workshop, a BLW computation of file.inp is obtained with the command "blwrun file " file.log and file.blw are in the current directory. |
| HuLiS : a Huckel-based code |
|---|
|
HuLiS is provided by Stephane Humbel (Aix-Marseille Université - France). This is a graphical java applet that deals with Huckel and Lewis structures. It computes coefficients and weights of mesomeric structures through two different approaches: the energy related approach is a simulated CI (HL-CI - deprecated); the wave function approach is a projection of Lewis structures onto a Huckel derived wave function(HLP). This second approach is more reliable. HuLiS is launch with the command "java -jar ~/bin/hulis.jar" or via the web site HuLiS Details of the principles are written at HL-CI and HLP explanations. Seminal papers are HL-CI and HLP. |
| Main exercises | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Exercice 1 (Lewis structures of benzene, resonance)
The 6-31G(d) basis set will be used in the following. 1/ Vertical Resonance Energy - at the geometry of benzene. With the BLW program, and using the provided optimized geometry of benzene molecule, define one 1,3,5-cyclohexadiene Lewis structure, and optimize it's orbitals. 4 blocks need to be defined : 3 blocks for 3 pi bond, and 1 for all the sigma electrons. Using benzene energy, calculate the Vertical Resonance Energy (VRE).
With the BLW program, relax the Lewis' structure geometry.
Exercice 2 (allyl)
Exercise 3 (BH3... NH3) electronics at the B3LYP 6-31G(d) levelBLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps.
|
| Optional exercises - homework | ||||||
|---|---|---|---|---|---|---|
Exercise 4 (Butadiene deconjugation without hyperconjugation)Examine the conjugation in planar butadiene and the hyperconjugation in perpendicular butadiene, and explain the rotational barrier. Note that often people rotate one participating group to disable the conjugation and use the barrier to measure the conjugation energy. What is the inconvenience of this approach?
FILES FOR THE BUTADIENE DECONJUGAISON Exercise 5 : formamide and allyl radical with HuLiSHere are two HuLiS exercices : find the weights in formamide with HL-CI and use HLP to get coefficients for the allyl radical. Formamide with HL-CIFormamide can be written as a resonance between two Lewis strutures. We shall find the weights of this scheme using HL-CI. In HL-CI we define an effective CI hamiltonian that concerns the interaction between the (localized) Lewis structures <math> \Psi_{I}</math> and <math> \Psi_{II}</math>: <math> \Psi_{HL-CI}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. This CI must give the Huckel energy of the delocalized wave function. <math> E_{HL-CI}=E_{Huckel}</math>
<math> \Psi_{HL-CI}=0.81\Psi_{I}+0.58\Psi_{II}</math>, hence the weights of the structures (I/II)=(66%/34%) Note that in HL-CI <math><\Psi_{I}|\Psi_{II}>=0</math>
Allyl Radical with HLPAllyl radical can be written as a resonance between two Lewis strutures: <math> \Psi_{HLP}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. We shall find the coefficients of this CI via HLP. The Huckel orbitals are considered as :
In the following the Huckel wave function is expressed as a Salter determinant: <math> \Psi_{Huckel}=|\phi_{1}\bar{\phi_{1}}\phi_2|</math> In the HLP scheme we search the coefficient of the structures I and II by projection of the Huckel wave function onto the localized structures <math> \Psi_{I}=|\pi_{12}\bar{\pi_{12}}p_3|</math> and <math>\Psi_{II}=|p_1\pi_{23}\bar{\pi_{23}}|</math>. Overlap between Lewis structuresWithin Huckel approximation, (<math> <p_{i}|p_{j}>=\delta_{ij}</math>)
Find <math>c_I</math> and <math>c_{II}</math> by solving the equations that derive from
This drawback can be shown using the energies of the occupied Huckel orbitals <math> \epsilon_1=\alpha+1.41\beta</math> and<math> \epsilon_2=\alpha</math> |