Différences entre les versions de « VBTutorial4 »
| (35 versions intermédiaires par 3 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | [[ | + | [[VB_tutorial|<<< VB tutorials main page]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Ligne 16 : | Ligne 7 : | ||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| − | ! | + | !<big>'''BLW within GAMESS (Version: MAR-25-2010 R2)'''</big> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | [[BLW | BLW ]] is provided by [http://homepages.wmich.edu/~ymo/ Yirong Mo] (Western Michigan University - USA). It allows to optimize local wave | + | [[BLW | BLW ]] is provided by [http://homepages.wmich.edu/~ymo/ Yirong Mo] (Western Michigan University - USA). It allows to optimize local wave functions. DFT approaches allow to include a part of correlation into the structure. |
| − | + | Gradients are available for geometry optimization. Structures can interact with $BLWCI group. | |
| − | |||
| − | Structures can interact with $BLWCI group. | ||
During the workshop, a BLW computation of file.inp is obtained with the command "blwrun file " | During the workshop, a BLW computation of file.inp is obtained with the command "blwrun file " | ||
| Ligne 57 : | Ligne 23 : | ||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| − | ! | + | !<big>'''HuLiS : a Huckel-based code'''</big> |
|- | |- | ||
| | | | ||
| Ligne 74 : | Ligne 40 : | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| − | !<big><big><big>''' | + | !<big><big><big>'''Main exercises'''</big></big></big> |
|- | |- | ||
| | | | ||
| Ligne 146 : | Ligne 59 : | ||
|} | |} | ||
| − | The | + | The 6-31G(d) basis set will be used in the following. |
1/ Vertical Resonance Energy - at the geometry of benzene. | 1/ Vertical Resonance Energy - at the geometry of benzene. | ||
| − | |||
| − | |||
| − | |||
| + | With the BLW program, and using the provided optimized geometry of benzene molecule, define one 1,3,5-cyclohexadiene Lewis structure, and optimize it's orbitals. 4 blocks need to be defined : 3 blocks for 3 pi bond, and 1 for all the sigma electrons. | ||
| + | Using benzene energy, calculate the Vertical Resonance Energy (VRE). | ||
| + | |||
| + | |||
| + | 2/ Adiabatic Resonance Energy (ARE)- relax the Lewis structure geometry | ||
| − | |||
With the BLW program, relax the Lewis' structure geometry. | With the BLW program, relax the Lewis' structure geometry. | ||
: Compare the C-C bond distances to benzene's. Ensure that it is consistent with the Lewis structure. | : Compare the C-C bond distances to benzene's. Ensure that it is consistent with the Lewis structure. | ||
| Ligne 162 : | Ligne 76 : | ||
3/ With HuLiS, evaluate the space spanned by Lewis structures compared to that of delocalized wave functions. | 3/ With HuLiS, evaluate the space spanned by Lewis structures compared to that of delocalized wave functions. | ||
| + | |||
: Draw the benzene with the Huckel tools (blue, left) and create two Kekules structures with the Lewis tools. Double bonds are obtained by clicking a single bond - A second click returns to the Single bond. | : Draw the benzene with the Huckel tools (blue, left) and create two Kekules structures with the Lewis tools. Double bonds are obtained by clicking a single bond - A second click returns to the Single bond. | ||
::Note the low value of the trust factor <math>{\tau}</math>. | ::Note the low value of the trust factor <math>{\tau}</math>. | ||
| Ligne 170 : | Ligne 85 : | ||
::Note the value of <math>{\tau}</math>, and the weight of all Lewis structures needed ([Results]). | ::Note the value of <math>{\tau}</math>, and the weight of all Lewis structures needed ([Results]). | ||
| − | [[VBFile 4-1 | | + | [[VBFile 4-1 | FILES FOR BENZENE]] |
== Exercice 2 (allyl) == | == Exercice 2 (allyl) == | ||
| Ligne 176 : | Ligne 91 : | ||
*1/ With the BLW code calculate the relative energies of the three Lewis structures of the allyl cation at the HF level. By comparison with the energy of the allyl cation, determine the VRE and the ARE. Compare the C-C bond distances. | *1/ With the BLW code calculate the relative energies of the three Lewis structures of the allyl cation at the HF level. By comparison with the energy of the allyl cation, determine the VRE and the ARE. Compare the C-C bond distances. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Hints''' | ||
| + | |- | ||
| + | | | ||
| + | * Starting from the delocalized geometry, the first iteration of the optimization of the localized structure will give the VRE. | ||
| + | |} | ||
*2/ Repeat the first question at the B3LYP level. | *2/ Repeat the first question at the B3LYP level. | ||
*3/ Repeat questions 1 and 2 for the allyl radical. | *3/ Repeat questions 1 and 2 for the allyl radical. | ||
| − | |||
| − | |||
[[VBFile 4-2 | FILES FOR THE ALLYLS]] | [[VBFile 4-2 | FILES FOR THE ALLYLS]] | ||
| − | == | + | == Exercise 3 (BH3... NH3) electronics at the B3LYP 6-31G(d) level == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
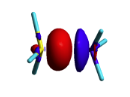
BLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps. | BLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps. | ||
| Ligne 284 : | Ligne 192 : | ||
don't forget to name the cube file. | don't forget to name the cube file. | ||
'''test.cube_BLW''' | '''test.cube_BLW''' | ||
| − | see also [[VBFile_4- | + | see also [[VBFile_4-3#gaussiancube.com | gaussiancube file]] |
| + | |||
| + | |} | ||
| + | |||
| + | [[VBFile 4-3 | FILES FOR THE NH3 ... BH3]] | ||
|} | |} | ||
| − | [[VBFile 4-4 | | + | |
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big><big><big>'''Optional exercises - homework'''</big></big></big> | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | == Exercise 4 (Butadiene deconjugation without hyperconjugation) == | ||
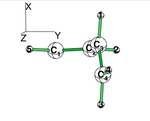
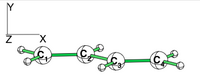
| + | [[File:Rotated_butadiene.png|right|150px|alt=butadiene - Lewis alt text | planar butadiene ]] | ||
| + | [[File:planar_butadiene.png|right|200px|alt=butadiene - Lewis alt text | planar butadiene ]] | ||
| + | Examine the conjugation in planar butadiene and the hyperconjugation in perpendicular butadiene, and explain the rotational barrier. | ||
| + | |||
| + | Note that often people rotate one participating group to disable the conjugation and use the barrier to measure the conjugation energy. What is the inconvenience of this approach? | ||
| + | |||
| + | |||
| + | * Compute the conjugated planar form with a standard B3LYP/6-31G(d) calculation | ||
| + | * Using BLW, localize the pi electrons on C1=C2 and on C3=C4 double bonds. (view the geometrie to verify that the pi system is along the X axis. | ||
| + | * Compare the energies to calculate the conjugaison energy. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Planar geometry''' | ||
| + | |- | ||
| + | | | ||
| + | <html><pre> | ||
| + | C 6.0 0.0000000000 0.6097325637 1.7490045499 | ||
| + | C 6.0 0.0000000000 0.6038280097 0.4085967284 | ||
| + | C 6.0 0.0000000000 -0.6038307169 -0.4085950903 | ||
| + | C 6.0 0.0000000000 -0.6097309803 -1.7490029472 | ||
| + | H 1.0 0.0000000000 1.5343833559 2.3190652626 | ||
| + | H 1.0 0.0000000000 -0.3149186339 2.3230080652 | ||
| + | H 1.0 0.0000000000 1.5514513284 -0.1322302753 | ||
| + | H 1.0 0.0000000000 -1.5514569088 0.1322266423 | ||
| + | H 1.0 0.0000000000 -1.5343794820 -2.3190677945 | ||
| + | H 1.0 0.0000000000 0.3149214640 -2.3230051413 | ||
| + | </pre></html> | ||
| + | |} | ||
| + | * Use the perpendicular form given below to compute the "deconjugated" system. The comparairison with the planar standard calculation gives an estimate of the conjugaison, which is contaminated by some hyperconjugaison. | ||
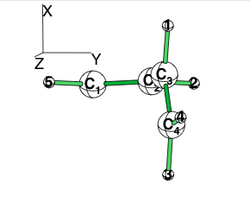
| + | * To inhibit hyperconjugaison in the perpendicular form, localize the electrons on the C1=C2 and on C3=C4 double bond. (note that the C3=C4 vinyl group has rotated along the XZ plane; hence its pi system is along the Y axis. | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Twisted (perpendicular) geometry''' | ||
| + | |- | ||
| + | | | ||
| + | |||
| + | <html><pre> | ||
| + | C 6.0 0.000000 -1.086858 2.236154 | ||
| + | C 6.0 0.000000 0.000000 1.489418 | ||
| + | C 6.0 0.000000 0.000000 0.000000 | ||
| + | C 6.0 -1.086858 0.000000 -0.746736 | ||
| + | H 1.0 0.967527 0.000000 -0.478451 | ||
| + | H 1.0 0.000000 0.967527 1.967869 | ||
| + | H 1.0 -2.072275 0.000000 -0.314213 | ||
| + | H 1.0 -1.029400 0.000000 -1.820913 | ||
| + | H 1.0 0.000000 -2.072275 1.803631 | ||
| + | H 1.0 0.000000 -1.029400 3.310331 | ||
| + | $END | ||
| + | |||
| + | </pre></html> | ||
| + | [[File:Rotated_butadiene.png|right|250px|alt=butadiene - Lewis alt text | planar butadiene The C3=C4 has rotated along the XZ plane; hence its pi system is along the Y axis.]] | ||
| + | |||
| + | |} | ||
| + | [[VBFile 4-4 | FILES FOR THE BUTADIENE DECONJUGAISON ]] | ||
| + | |||
| + | == Exercise 5 : formamide and allyl radical with HuLiS == | ||
| + | |||
| + | Here are two HuLiS exercices : find the weights in formamide with HL-CI and use HLP to get coefficients for the allyl radical. | ||
| + | |||
| + | ====Formamide with HL-CI==== | ||
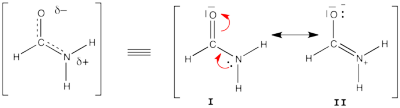
| + | [[File:Formamide.png|400px|thumb|right]] | ||
| + | Formamide can be written as a resonance between two Lewis strutures. We shall find the weights of this scheme using HL-CI. | ||
| + | |||
| + | In HL-CI we define an effective CI hamiltonian that concerns the interaction between the (localized) Lewis structures <math> \Psi_{I}</math> and <math> \Psi_{II}</math>: <math> \Psi_{HL-CI}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. This CI must give the Huckel energy of the delocalized wave function. <math> E_{HL-CI}=E_{Huckel}</math> | ||
| + | |||
| + | *1/ Write the expression of the CI secular determinant that has the energy ot the delocalized wave function, and show that the off-diagonal term is <math>H_{I-II}=0.71\beta</math>. (in HL-CI the off diagonal term is supposed <0). | ||
| + | |||
| + | *2/ Resolve the secular equations of the CI and find that | ||
| + | <math> \Psi_{HL-CI}=0.81\Psi_{I}+0.58\Psi_{II}</math>, hence the weights of the structures (I/II)=(66%/34%) | ||
| + | |||
| + | Note that in HL-CI <math><\Psi_{I}|\Psi_{II}>=0</math> | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''help''' | ||
| + | |- | ||
| + | | | ||
| + | Formamide's Huckel energy <math>E_{Huckel}= 4\alpha + 6.548\beta</math> | ||
| + | |||
| + | The (localized) Lewis structures '''I''' and '''II''' have an energy of | ||
| + | ** <math>E_{I}= 2*(\alpha + 1.370\beta)+2*(\alpha+1.651\beta)= 4\alpha + 6.041\beta</math> | ||
| + | ** <math>E_{II}= 2*(\alpha + 1.808\beta)+2*(\alpha+0.970\beta)= 4\alpha + 5.556\beta</math> | ||
| + | |||
| + | These values are used as <math>H_{I-I}</math> and <math>H_{II-II}</math> for the CI matrix. | ||
| + | |} | ||
| + | |||
| + | ====Allyl Radical with HLP==== | ||
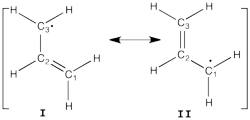
| + | [[File:Allyl_radical.png|250px|thumb|right]] | ||
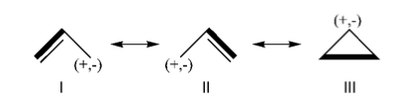
| + | Allyl radical can be written as a resonance between two Lewis strutures: <math> \Psi_{HLP}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. | ||
| + | We shall find the coefficients of this CI via HLP. The Huckel orbitals are considered as : | ||
| + | |||
| + | ** <math> \phi_1=0.5 p_1 + 0.7 p_2 + 0.5 p_3 </math> | ||
| + | ** <math> \phi_2=0.7 p_1 + 0.0 p_2 - 0.7 p_3 </math> | ||
| + | ** <math> \phi_3=0.5 p_1 - 0.7 p_2 + 0.5 p_3 </math> | ||
| + | In the following the Huckel wave function is expressed as a Salter determinant: <math> \Psi_{Huckel}=|\phi_{1}\bar{\phi_{1}}\phi_2|</math> | ||
| + | In the HLP scheme we search the coefficient of the structures I and II by projection of the Huckel wave function onto the localized structures <math> \Psi_{I}=|\pi_{12}\bar{\pi_{12}}p_3|</math> and <math>\Psi_{II}=|p_1\pi_{23}\bar{\pi_{23}}|</math>. | ||
| + | ======Overlap between Lewis structures ====== | ||
| + | Within Huckel approximation, (<math> <p_{i}|p_{j}>=\delta_{ij}</math>) | ||
| + | *1/ Find that <math> <\Psi_{I}|\Psi_{II}>=-0.25</math>. | ||
| + | *2/ Suppose that <math> <\Psi_{I}|\Psi_{Huckel}>=-0.73</math> and <math><\Psi_{II}|\Psi_{Huckel}>=+0.73</math>. | ||
| + | Find <math>c_I</math> and <math>c_{II}</math> by solving the equations that derive from | ||
| + | **<math><\Psi_I|\Psi_{Huckel}>=<\Psi_I|\Psi_{HLP}></math> | ||
| + | **<math><\Psi_{II}|\Psi_{Huckel}>=<\Psi_{II}|\Psi_{HLP}></math> | ||
| + | *3/ Compute the trust factor <math>\tau=<\Psi_{HLP}|\Psi_{huckel}></math> | ||
| + | |||
| + | *4/ Remark: HL-CI fails to give the correct signs because it supposes <math>H_{I-II}<0</math>. | ||
| + | This drawback can be shown using the energies of the occupied Huckel orbitals <math> \epsilon_1=\alpha+1.41\beta</math> and<math> \epsilon_2=\alpha</math> | ||
|} | |} | ||
Dernière version du 14 février 2013 à 08:27
BLW method & HuLiS program
| BLW within GAMESS (Version: MAR-25-2010 R2) |
|---|
|
BLW is provided by Yirong Mo (Western Michigan University - USA). It allows to optimize local wave functions. DFT approaches allow to include a part of correlation into the structure. Gradients are available for geometry optimization. Structures can interact with $BLWCI group. During the workshop, a BLW computation of file.inp is obtained with the command "blwrun file " file.log and file.blw are in the current directory. |
| HuLiS : a Huckel-based code |
|---|
|
HuLiS is provided by Stephane Humbel (Aix-Marseille Université - France). This is a graphical java applet that deals with Huckel and Lewis structures. It computes coefficients and weights of mesomeric structures through two different approaches: the energy related approach is a simulated CI (HL-CI - deprecated); the wave function approach is a projection of Lewis structures onto a Huckel derived wave function(HLP). This second approach is more reliable. HuLiS is launch with the command "java -jar ~/bin/hulis.jar" or via the web site HuLiS Details of the principles are written at HL-CI and HLP explanations. Seminal papers are HL-CI and HLP. |
| Main exercises | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Exercice 1 (Lewis structures of benzene, resonance)
The 6-31G(d) basis set will be used in the following. 1/ Vertical Resonance Energy - at the geometry of benzene. With the BLW program, and using the provided optimized geometry of benzene molecule, define one 1,3,5-cyclohexadiene Lewis structure, and optimize it's orbitals. 4 blocks need to be defined : 3 blocks for 3 pi bond, and 1 for all the sigma electrons. Using benzene energy, calculate the Vertical Resonance Energy (VRE).
With the BLW program, relax the Lewis' structure geometry.
Exercice 2 (allyl)
Exercise 3 (BH3... NH3) electronics at the B3LYP 6-31G(d) levelBLW energy decomposition analysis can be used to shed light into the nature of intermolecular interactions. Example of NH3∙∙∙BH3. Visualize the polarization and electron transfer effects using the electron density difference (EDD) maps.
|
| Optional exercises - homework | ||||||
|---|---|---|---|---|---|---|
Exercise 4 (Butadiene deconjugation without hyperconjugation)Examine the conjugation in planar butadiene and the hyperconjugation in perpendicular butadiene, and explain the rotational barrier. Note that often people rotate one participating group to disable the conjugation and use the barrier to measure the conjugation energy. What is the inconvenience of this approach?
FILES FOR THE BUTADIENE DECONJUGAISON Exercise 5 : formamide and allyl radical with HuLiSHere are two HuLiS exercices : find the weights in formamide with HL-CI and use HLP to get coefficients for the allyl radical. Formamide with HL-CIFormamide can be written as a resonance between two Lewis strutures. We shall find the weights of this scheme using HL-CI. In HL-CI we define an effective CI hamiltonian that concerns the interaction between the (localized) Lewis structures <math> \Psi_{I}</math> and <math> \Psi_{II}</math>: <math> \Psi_{HL-CI}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. This CI must give the Huckel energy of the delocalized wave function. <math> E_{HL-CI}=E_{Huckel}</math>
<math> \Psi_{HL-CI}=0.81\Psi_{I}+0.58\Psi_{II}</math>, hence the weights of the structures (I/II)=(66%/34%) Note that in HL-CI <math><\Psi_{I}|\Psi_{II}>=0</math>
Allyl Radical with HLPAllyl radical can be written as a resonance between two Lewis strutures: <math> \Psi_{HLP}=c_{I}\Psi_{I}+c_{II}\Psi_{II}</math>. We shall find the coefficients of this CI via HLP. The Huckel orbitals are considered as :
In the following the Huckel wave function is expressed as a Salter determinant: <math> \Psi_{Huckel}=|\phi_{1}\bar{\phi_{1}}\phi_2|</math> In the HLP scheme we search the coefficient of the structures I and II by projection of the Huckel wave function onto the localized structures <math> \Psi_{I}=|\pi_{12}\bar{\pi_{12}}p_3|</math> and <math>\Psi_{II}=|p_1\pi_{23}\bar{\pi_{23}}|</math>. Overlap between Lewis structuresWithin Huckel approximation, (<math> <p_{i}|p_{j}>=\delta_{ij}</math>)
Find <math>c_I</math> and <math>c_{II}</math> by solving the equations that derive from
This drawback can be shown using the energies of the occupied Huckel orbitals <math> \epsilon_1=\alpha+1.41\beta</math> and<math> \epsilon_2=\alpha</math> |