Différences entre les versions de « The SD BOVB method »
| (12 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 6 : | Ligne 6 : | ||
=== Definition of the S-BOVB level === | === Definition of the S-BOVB level === | ||
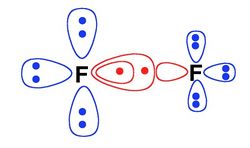
| − | + | "S" is the acronym for "split". At this level, in each VB structure, all the active orbitals which are doubly occupied at the L-BOVB level are "split", i.e. they are replaced by a pair of singlet-coupled electrons in two ''different'' orbitals located on the same center. Here is below a pictorial example for the F<sup>-</sup>F<sup>+</sup> ionic structure of difluorine dimer. This allows for the inclusion of some radial correlation within the active electron pairs. | |
<center>[[File:F%2BF-.jpg|250px]]</center> | <center>[[File:F%2BF-.jpg|250px]]</center> | ||
| Ligne 12 : | Ligne 12 : | ||
=== How to proceed - HF example === | === How to proceed - HF example === | ||
| − | To go from the L-BOVB to the | + | To go from the L-BOVB to the SL-BOVB level, one has to prepare a guess, that will be obtained by transforming a former guess arising from a converged LBOVB calculation. The transformation is done manually by first duplicating each active doubly occupied orbital of the VB structure that is to be described at the SL-BOVB level. Then, for each lone pair, one of the split orbital is manually made more compact, an the other more diffuse, by playing with the coefficients of the basis functions (modifying the coefficient value by ±0.2 for instance). This does not need to be done accurately (this is only a guess). A convenient way of doing this is to play only with the largest coefficient of the orbital, leaving the other ones unchanged. Once this guess is prepared, the two electrons of each split lone pair are coupled in a singlet way in the input, and the optimizization of this wave function is launched '''''freezing the inactive orbitals'''''. |
| − | + | An example of SL-BOVB calculation on the HF molecule can be found in the following directory : | |
| − | + | EXERCISES/TUTORIAL1/EXERCISE1/question2/answer/.S-BOVB | |
| + | Thus, the input for the SL-BOVB calculation is in … answer/.SBOVB/hf-sbovb.xmi, and the guess for running the corresponding calculation is in …answer/.SBOVB/hf-sbovb.gus. This latter guess is obtained by transforming the .orb file of the converged L-BOVB calculation, which can be found in …/answer/ hf-lbovb.orb. | ||
| − | + | It can be seen that the SL-BOVB wave function is lower than the L-BOVB one by ~5 kcal/mol. As both wave functions dissociate to the same limit (H plus F atoms calculated separately at the ROHF level), the improvement on the total energy carries over to the bonding energy, which is found greater at the SL-BOVB than at the L-BOVB level. | |
=== IMPORTANT WARNINGS === | === IMPORTANT WARNINGS === | ||
| − | * The | + | * The SL-BOVB and SD-BOVB are better suited for users already having a good experience of calculations at the L- and D-BOVB simpler levels. |
| − | * It is | + | * It is important to start from a good guess, in order to avoid misconvergence or, even worse, convergence on secondary minima or unphysical solutions. In particular : |
| − | ** the "boys" keyword | + | ** It is advisable to use the "boys" keyword at the initial VBSCF level, as it will ensures that the split orbitals indeed correspond to the active lone pair that you wish to split, and not an inactive pair sharing the same orbital definition (for instance : to distinguish between the 2s lone pair of Fluorine and the sigma active orbital in F2 or HF molecules). |
| − | ** a converged L-BOVB solution must be used as a guess for the S-BOVB level | + | ** a converged L-BOVB solution must be used as a guess for the S-BOVB level |
| − | |||
=== SD-BOVB calculations === | === SD-BOVB calculations === | ||
| Ligne 32 : | Ligne 32 : | ||
# perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while '''''freezing the inactive orbitals''''' during the optimization (put "0" as coefficient in first $orb line) ; | # perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while '''''freezing the inactive orbitals''''' during the optimization (put "0" as coefficient in first $orb line) ; | ||
# then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while '''''freezing the active orbitals''''' during the optimization (put "0" as coefficient in first $orb line). | # then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while '''''freezing the active orbitals''''' during the optimization (put "0" as coefficient in first $orb line). | ||
| + | |||
| + | As an example, see the SD-BOVB calculation on the F<sub>2</sub> molecule in the tutorial machines here : | ||
| + | |||
| + | EXERCISES/TUTORIAL1/EXERCISE2/question2/answer/.SD-BOVB | ||
| + | |||
| + | We obtain a bonding energy of 37.1 kcal/mol at the SD-BOVB level using the 6-31G(d) basis set, already very close to the estimated exact value of 39.0 kcal/mol. | ||
| + | |||
====High symmetry case:==== | ====High symmetry case:==== | ||
# Perform a π-D-VBSCF calculation '''together with the keyword ''boys'' ''' in the $orb section ; | # Perform a π-D-VBSCF calculation '''together with the keyword ''boys'' ''' in the $orb section ; | ||
| Ligne 41 : | Ligne 48 : | ||
As an example, see the π-SD-BOVB calculation on the F<sub>2</sub> molecule in the tutorial machines here : | As an example, see the π-SD-BOVB calculation on the F<sub>2</sub> molecule in the tutorial machines here : | ||
| − | EXERCISES/TUTORIAL1/ | + | EXERCISES/TUTORIAL1/EXERCISE2/question2/answer/.PI-SD-BOVB |
| − | + | You may compare these calculations to the previous example. | |
---- | ---- | ||
Dernière version du 28 août 2012 à 10:21
<<< Back to the "general guidelines for BOVB calculations"
Definition of the S-BOVB level
"S" is the acronym for "split". At this level, in each VB structure, all the active orbitals which are doubly occupied at the L-BOVB level are "split", i.e. they are replaced by a pair of singlet-coupled electrons in two different orbitals located on the same center. Here is below a pictorial example for the F-F+ ionic structure of difluorine dimer. This allows for the inclusion of some radial correlation within the active electron pairs.
How to proceed - HF example
To go from the L-BOVB to the SL-BOVB level, one has to prepare a guess, that will be obtained by transforming a former guess arising from a converged LBOVB calculation. The transformation is done manually by first duplicating each active doubly occupied orbital of the VB structure that is to be described at the SL-BOVB level. Then, for each lone pair, one of the split orbital is manually made more compact, an the other more diffuse, by playing with the coefficients of the basis functions (modifying the coefficient value by ±0.2 for instance). This does not need to be done accurately (this is only a guess). A convenient way of doing this is to play only with the largest coefficient of the orbital, leaving the other ones unchanged. Once this guess is prepared, the two electrons of each split lone pair are coupled in a singlet way in the input, and the optimizization of this wave function is launched freezing the inactive orbitals.
An example of SL-BOVB calculation on the HF molecule can be found in the following directory :
EXERCISES/TUTORIAL1/EXERCISE1/question2/answer/.S-BOVB
Thus, the input for the SL-BOVB calculation is in … answer/.SBOVB/hf-sbovb.xmi, and the guess for running the corresponding calculation is in …answer/.SBOVB/hf-sbovb.gus. This latter guess is obtained by transforming the .orb file of the converged L-BOVB calculation, which can be found in …/answer/ hf-lbovb.orb.
It can be seen that the SL-BOVB wave function is lower than the L-BOVB one by ~5 kcal/mol. As both wave functions dissociate to the same limit (H plus F atoms calculated separately at the ROHF level), the improvement on the total energy carries over to the bonding energy, which is found greater at the SL-BOVB than at the L-BOVB level.
IMPORTANT WARNINGS
- The SL-BOVB and SD-BOVB are better suited for users already having a good experience of calculations at the L- and D-BOVB simpler levels.
- It is important to start from a good guess, in order to avoid misconvergence or, even worse, convergence on secondary minima or unphysical solutions. In particular :
- It is advisable to use the "boys" keyword at the initial VBSCF level, as it will ensures that the split orbitals indeed correspond to the active lone pair that you wish to split, and not an inactive pair sharing the same orbital definition (for instance : to distinguish between the 2s lone pair of Fluorine and the sigma active orbital in F2 or HF molecules).
- a converged L-BOVB solution must be used as a guess for the S-BOVB level
SD-BOVB calculations
General case (low symmetry):
- Perform a ("L") VBSCF calculation together with the keyword boys in the $orb section ;
- perform the L-BOVB calculation, starting from converged VBSCF orbitals ;
- perform the S-BOVB calculation : starting from the converged L-BOVB orbital as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while freezing the inactive orbitals during the optimization (put "0" as coefficient in first $orb line) ;
- then perform the SD-BOVB calculation : starting from the converged S-BOVB orbitals as guess, run the calculation by optimizing the delocalized inactive orbitals, while freezing the active orbitals during the optimization (put "0" as coefficient in first $orb line).
As an example, see the SD-BOVB calculation on the F2 molecule in the tutorial machines here :
EXERCISES/TUTORIAL1/EXERCISE2/question2/answer/.SD-BOVB
We obtain a bonding energy of 37.1 kcal/mol at the SD-BOVB level using the 6-31G(d) basis set, already very close to the estimated exact value of 39.0 kcal/mol.
High symmetry case:
- Perform a π-D-VBSCF calculation together with the keyword boys in the $orb section ;
- perform a π-D-BOVB calculation, starting from converged VBSCF orbitals ;
- perform the π-SD-BOVB calculation in two steps :
- step1 : starting from the converged π-D-BOVB orbitals as guess with splitted and modified doubly occupied active pairs as explained above, run the calculation by optimizing the active orbitals, while freezing the inactive orbitals during the optimization (put "0" as coefficient in first $orb line) ;
- step2 : then restarting from the converged orbitals obtained at the previous step, optimizing all orbitals (both active and inactive) at the same time.
As an example, see the π-SD-BOVB calculation on the F2 molecule in the tutorial machines here :
EXERCISES/TUTORIAL1/EXERCISE2/question2/answer/.PI-SD-BOVB
You may compare these calculations to the previous example.