Différences entre les versions de « VBTutorial3 »
| Ligne 34 : | Ligne 34 : | ||
== Exercice 1 (paper exercice) : Conical intersection in H3. radical == | == Exercice 1 (paper exercice) : Conical intersection in H3. radical == | ||
| − | Consider three hydrogen atoms Ha, Hb, Hc, with respective atomic orbitals a, b and c, and the two VB structures | + | Consider three hydrogen atoms Ha, Hb, Hc, with respective atomic orbitals a, b and c, and the two VB structures [[File:image_1.png|150px]]] and [[File:P.png|150px]]] . |
| + | |||
| + | The Ha-Hb and Hb-Hc distances are equal. [[Image:image_3.png|120px]] | ||
| − | # By using the thumb rules recalled below, where squared overlap terms are neglected, derive the expression of the energies of R and P, and of the reduced Hamiltonian matrix element between R and P for the 3-orbital/3-electrons reacting system [Ha--Hb--Hc]•. | + | # By using the thumb rules recalled below, where squared overlap terms are neglected, derive the expression of the energies of R and P, and of the reduced Hamiltonian matrix element between R and P for the 3-orbital/3-electrons reacting system [Ha--Hb--Hc]•. |
| − | # From the sign of this latter integral when θ > 60°, derive the expressions of the ground state | + | # From the sign of this latter integral when θ > 60°, derive the expressions of the ground state Ψ<sup>≠</sup> and of the first excited state Ψ* of the H<sub>3</sub>• system. One may drop the normalization constants for simplicity. What bonding scheme does the excited state represent ? |
# Show that the reduced Hamiltonian matrix element is largest in the collinear transition state geometry, and drops to zero in the equilateral triangular structure. | # Show that the reduced Hamiltonian matrix element is largest in the collinear transition state geometry, and drops to zero in the equilateral triangular structure. | ||
# Show that R and P VB structures are degenerate in the equilateral triangular structure, and that Ψ≠ and Ψ* are also degenerate in this geometry. | # Show that R and P VB structures are degenerate in the equilateral triangular structure, and that Ψ≠ and Ψ* are also degenerate in this geometry. | ||
| Ligne 43 : | Ligne 45 : | ||
'''Appendix : Thumb rules for the calculations of effective Hamiltonian matrix elements between determinants.''' | '''Appendix : Thumb rules for the calculations of effective Hamiltonian matrix elements between determinants.''' | ||
| − | # Energy of a determinant D : . | + | # Energy of a determinant D : [[File:E(D).png|120px]]] (if orbitals i and j have parallel spins) |
| − | # Matrix element between determinants differing by spin inversion of two spin-orbitals : | + | # Matrix element between determinants differing by spin inversion of two spin-orbitals :[[File:Hij.png|220px]]] |
[[Answer Exercise 1 of tutorial 3|>> Answer]] | [[Answer Exercise 1 of tutorial 3|>> Answer]] | ||
Version du 1 juin 2012 à 09:52
How to modify this page :
- first : log in (top right of this page) ;
- click on [edit] (far right) to edit a section of the page ;
- write your text directly in the wiki page, and click on the "Save page" button (bottom left) to save your modifications
Pictures : how to insert a picture in your text
See also this page for an introduction to the basics of the wiki syntax
To the Tutors
Sason remarks and prospective 2 hours talk +
Philippe's remark on the initially proposed tutorial. are included in bold.
Qualitative
- State correlation Diagrams in 3 centers systems : H3C. - H. - .CH3 (or 4 electrons .... H transfer barrier appearing in F H F(-) when the F ... F distance is increased (which avoids geometry problems).
Yes, but we could start with H3
- Benzen pi system dissymetrization (2 geometries (D6h and D3h); on each geometry 2 spin alternant determinants cf p154 on The Book) - Pbm : check how differentiate sigma vs + (sigma + pi) energies.
Objection : Using two spin-alternant determinants refers to Heisenberg’s spin hamiltonian theory, that we don’t teach. Differentiating sigma vs sigma + pi energies is a bit off-topic.
Exercices
Exercice 1 (paper exercice) : Conical intersection in H3. radical
Consider three hydrogen atoms Ha, Hb, Hc, with respective atomic orbitals a, b and c, and the two VB structures 
] and 
] .
The Ha-Hb and Hb-Hc distances are equal. 
- By using the thumb rules recalled below, where squared overlap terms are neglected, derive the expression of the energies of R and P, and of the reduced Hamiltonian matrix element between R and P for the 3-orbital/3-electrons reacting system [Ha--Hb--Hc]•.
- From the sign of this latter integral when θ > 60°, derive the expressions of the ground state Ψ≠ and of the first excited state Ψ* of the H3• system. One may drop the normalization constants for simplicity. What bonding scheme does the excited state represent ?
- Show that the reduced Hamiltonian matrix element is largest in the collinear transition state geometry, and drops to zero in the equilateral triangular structure.
- Show that R and P VB structures are degenerate in the equilateral triangular structure, and that Ψ≠ and Ψ* are also degenerate in this geometry.
- We now extend the above conclusions to the allyl radical. What are the bonding schemes corresponding to the ground state and first excited state ? What geometrical distortion would make these two states degenerate ? What would be the end product of a photochemical excitation of allyl radical to its first excited state ?
Appendix : Thumb rules for the calculations of effective Hamiltonian matrix elements between determinants.
- Energy of a determinant D :
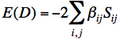] (if orbitals i and j have parallel spins) - Matrix element between determinants differing by spin inversion of two spin-orbitals :
]
.png){kind=small}
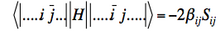Exercice 2 : computation of X—X + X. -> X. + X—X radical exchange VBSCD diagram for X=H,Li
- Paper exercice :
- Beginning of ex. 6.3 from Sason & Philippe's book (first 3 lines)
- Exercice 6.5 from Sason & Philippe's book
- Exercice 6.6 questions a),b) and c)
- Exercice 6.6 question d)
- Exercice 6.6 question e)
- Computer exercise :
idea : Compute VBSCD diagrams for X—X + X. -> X. + X—X X=H, Li at VBSCF then VBCI level. To be written...
Exercice 3 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system
Sason's remark :
" F(-) + H-F example is not good by itself, unless you also do F• + H-F - showing that in one case you have an intermediate FHF(-) and in the other case you have a high barrier.
If we just want to do one case of 4-electron/3-center reaction, we should use Cl(-) + CH3Cl.
The audience will appreciate a more chemical example, which is Cl(-) + CH3Cl. "
Benoît's proposition :
- Paper exercice :
- Exercice 6.12 question a) (from Sason & Philippe's book)
- Exercice 6.12 question b)
- Computer exercise :
idea : Compute VBSCD diagrams for Cl(-) + CH3Cl -> ClCH3 + Cl(-), at D-BOVB levels, first in gas phase then using VB(PCM)... Which basis set should we use : 6-31+G*. As this is an anion we should add a set of diffuse functions, but then there may be trouble with BOVB... Check first that everything is fine at BOVB level (no instability)...