VBTutorial3

<< Return to the program

How to modify this page :

• first : log in (top right of this page) ;
• click on [edit] (far right) to edit a section of the page ;
• write your text directly in the wiki page, and click on the "Save page" button (bottom left) to save your modifications

Pictures : how to insert a picture in your text

See also this page for an introduction to the basics of the wiki syntax

State correlation diagrams

Remarks

>> Initial remarks for tutors

Exercises

Main Exercise

Exercise 1 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system

• Computer exercise :

In this exercise the <math>\textrm{S}_{\textrm{N}}2</math> reaction Cl<math>{}^{-}</math> + CH3Cl -> ClCH3 + Cl<math>{}^{-}</math> will be computed in both vacuum and solution, at <math>\pi</math>-D-BOVB level. The basis set is DZP. The inner orbitals in Cl and C are described with MCP psedudo potential. Only reactant and transition state will be computed in this exercise. There are also optional calculations for the advanced users where 6-31+G* is used.

Note:How to perform a VBPCM calculation

A VBPCM calculation is performed in the similar way as the VB calculations in vacuum. One should prepare a GAMESS input file with solvent assigned such as:

$PCM SOLVNT=WATER $END

The details of PCM calculation in GAMESS can be found in GAMESS manual. Keyword "VBTYP=XMVB" in CONTRL section is also essential. After the GAMESS input file is prepared, an XMI file with keyword "VBPCM" should be prepared with the same file name as GAMESS input file. In current XMVB package, VBSCF/PCM and BOVB/PCM calculations are both supported.

Compute the Energies and Wavefunctions at Reactant and Transition State with Different Set of VB Structures

1. Write the following VB structure sets, compare and see the differences:
   1. all structures;
   2. minimal structures for reactant;
   3. minimal structures for product.
2. Perform <math>\pi</math>-D-BOVB calculation for reactant(see "high symmetry cases" here):
   1. Perform all-structure <math>\pi</math>-D-BOVB calculation as following:
      1. Perform L-VBSCF calculation with "orbtyp=hao frgtyp=sao guess=mo" and the orbitals are all localized on the Cl and CH<math>{}_3</math> groups;
      2. Perform D-VBSCF calculation where <math>\pi</math> oribtals are delocalized in the whole system and the <math>\sigma</math> orbitals are kept localized. Use the L-VBSCF orbitals as initial guess;
      3. Perform D-BOVB calculation with D-VBSCF orbital as initial guess.
   2. Perform <math>\pi</math>-D-BOVB calculations with minimal structures for reactant and product with the same procedure as all-structure calculation.
3. Perform <math>\pi</math>-D-BOVB calculation for transition state. The procedure is the same as step 2.
4. Perform <math>\pi</math>-D-BOVB/PCM calculations for reactant:
   1. Perform all-structure <math>\pi</math>-D-BOVB/PCM calculation for the reactant in following steps:
      1. Perform L-VBSCF/PCM calculation with L-VBSCF orbitals as initial guess;
      2. Perform D-VBSCF/PCM calculation with L-VBSCF/PCM orbitals as initial guess;
      3. Perform D-BOVB/PCM calculation with D-VBSCF/PCM orbitals as initial guess.
   2. Perform <math>\pi</math>-D-BOVB/PCM calculations with minimal structures for reactant and product in the sames steps as all structure calculation.
5. Perform BOVB/PCM calculations for transition state with the same procedure as in step 4.

Analyze the Data from Above Computations

1. Compute the Barrier height of the <math>\textrm{S}_{\textrm{N}}2</math> reaction in both vacuum and solution. See the difference of the barrier heights, and find out the reason.
2. Compare the energies of reactant and product structures at reactant and transition state, in both vacuum and solution. What's the difference of the energies at different points? Why?
3. Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies.

Optional Calculations for Advanced Users : Reactant and Transistion State of <math>\textrm{S}_{\textrm{N}}2</math> reaction with 6-31+G* basis set

These calculations are performed with 6-31+G* basis set and BFI section. The inner orbitals are frozen as HF orbitals in all VB calculations and the valence basis functions are reorganized to hybrid basis functions so that the <math>\sigma</math>, <math>\pi_x</math> and <math>\pi_y</math> spaces can be separated well. A D-BOVB calculation is performed in 2 steps:

1. Perform a VBSCF calculation with <math>\pi</math> orbitals delocalized in the whole system and <math>\sigma</math> orbitals localized on the Cl and CH<math>{}_3</math> groups;
2. Perform a BOVB calculation with VBSCF orbitals as initial guess.

The VB calculations are the same as the calculations performed above. Try to understand the BFI section, perform the calculations and compare the differences of barrier heights, resonance energies and performances with and without $BFI.

>> Answer

>> general guidelines for BOVB calculations

Optional Exercises

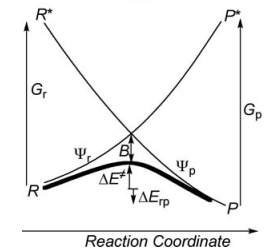
Exercise 2 : computation of H—H + H. -> H. + H—H radical exchange VBSCD diagram

1/ Paper exercise :

a/ Considering the following radical exchange process: <math> X^{\bullet} + A-Y \rightarrow X-A + ^{\bullet}Y </math> (X = A = Y = hydrogen atom)

Write the HL wave functions for R and R* and derive the value of G using semiempirical VB theory. Hints : 1) write the wave functions of R and R* so that their overlap is positive; 2) neglect the overlap beween the external atoms X and Y, and neglect the overlap between two different determinants.

b/ Considering the following reaction: <math> X^{\bullet} + H-X \rightarrow X-H +^{\bullet}X </math>
Use semiempirical VB theory to derive the following expression for the avoided crossing term <math> B </math> :
<math>B = 0.25\Delta E_{ST} </math>' where <math>\Delta E_{ST} </math>' is the singlet-triplet transition energy of the X-H bond at the geometry of the transitions state.
Indication: the resonance energy arising from the mixing of two degenerate VB structures is given by the following expression:

<math>RE = [H_{12}-E_{ind}S_{12}]/(1+S_{12}) </math>

where <math> E_{ind} </math> is the energy of an individual VB structure, and <math> S_{12} </math> and <math> H_{12} </math> are respectively the overlap and Hamiltonian matrix element between R and R*.

c/ It is known that for strong binders, at any given bonding distance the singlet-triplet transition energy is larger than twice the bonding energy of the dimer at equilibrium distance, so that one can write the approximate expression <math>\Delta E_{ST} </math>' <math> = 2 BDE </math>, where <math> BDE </math> is the bonding energy of the dimer at equilibrium distance. Using the latter expression, express the avoided crossing term <math> B </math> as a function of the bonding energy of <math> H_{2}</math>.

2/ Computer exercise :VBSCD for H—H + H. -> H. + H—H at VBSCF then VBCISD level.

In this exercise the VBSCD for H—H + H. -> H. + H—H at VBSCF then VBCISD level will be computed with 6-31G**. Computations for reactant and transition state are requested and other points are optional for advanced users.

Compute the Energies and Wavefunctions at Reactant and Transition State with Different Set of VB Structures

1. Write the following VB structure sets, compare and see the difference:
   1. all structures;
   2. minimal structures for reactant;
   3. minimal structures for product.
2. Perform VBSCF and VBCISD calculations for reactant:
   1. Perform a VBSCF calculation with "orbtyp=hao" and "boys";
   2. Perform a VBCISD calculation with VBSCF orbital as initial guess.
   3. Perform VBSCF and VBCISD calculations with minimal structures for reactant and product.
3. Perform VBSCF and VBCISD calculations for transition state with the same procedure as in step 2.

Analyze the Data from Above Computations

1. Compute the Barrier height of the <math>\textrm{S}_{\textrm{N}}2</math> reaction at VBSCF and VBCISD levels. See the difference of the barrier heights.
2. Compare the energies for reactant and product structures at reactant and transition state, by both VBSCF and VBCISD. What's the difference of the energies at different points? Why?
3. Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies.

Optional : Compute all points and draw the VBSCDs at VBSCF and VBCISD levels.

>> Answer

Exercise 3 (paper exercise) : Conical intersection in H₃^• radical

(for further reading, see S. Shaik and P.C. Hiberty, "The Chemist's Guide to VB theory", Wiley, Hoboken, New Jersey, 2008, pp. 157-161, exercises 6.11-6.14 pp. 174-176, and answers to the exercises pp. 188-192.

Consider three hydrogen atoms Ha, Hb, Hc, with respective atomic orbitals a, b and c, and the two VB structures ] and ] .

The Ha-Hb and Hb-Hc distances are equal.

1. By using the thumb rules recalled below, where squared overlap terms are neglected, derive the expression of the energies of R and P, and of the reduced Hamiltonian matrix element between R and P for the 3-orbital/3-electrons reacting system [Ha--Hb--Hc]•.
2. From the sign of this latter integral when θ > 60°, derive the expressions of the ground state Ψ^≠ and of the first excited state Ψ* of the H₃• system. One may drop the normalization constants for simplicity. What bonding scheme does the excited state represent ?
3. Show that the reduced Hamiltonian matrix element is largest in the collinear transition state geometry, and drops to zero in the equilateral triangular structure.
4. Show that R and P VB structures are degenerate in the equilateral triangular structure, and that Ψ≠ and Ψ* are also degenerate in this geometry.
5. We now extend the above conclusions to the allyl radical. What are the bonding schemes corresponding to the ground state and first excited state ? What geometrical distortion would make these two states degenerate ? What would be the end product of a photochemical excitation of allyl radical to its first excited state ?

Appendix : Thumb rules for the calculations of effective Hamiltonian matrix elements between determinants.

1. Energy of a determinant D : ] (if orbitals i and j have parallel spins)
2. Matrix element between determinants differing by spin inversion of two spin-orbitals :]

>> Answer