VBTutorial1

<< Return to the program

How to modify this page :

• first : log in (top right of this page) ;
• click on [edit] (far right) to edit a section of the page ;
• write your text directly in the wiki page, and click on the "Save page" button (bottom left) to save your modifications

Pictures : how to insert a picture in your text

See also this page for an introduction to the basics of the wiki syntax

Basics of VB theory and XMVB program

Remarks

>> Initial remarks for tutors

Exercises

Exercise 1 (paper exercise) : The lone pairs of H₂O

***** EXERCISE COMPLETED *****

(for further reading, see S. Shaik and P.C. Hiberty, "The Chemist's Guide to VB theory", Wiley, Hoboken, New Jersey, 2008, pp. 107-109)

This exercise aims at comparing two descriptions of the lone pairs of H<math>{}_2</math>O : (i) the MO description in terms of non-equivalent canonical MOs and (ii) the « rabbit-ear » VB description in terms of two equivalent hybrid orbitals.

<math>\Psi_{\textrm{MO}}</math>   <math>\Psi_{\textrm{VB}}</math>

1. Focusing on the lone pairs only, write the four-electron single-determinants <math>\Psi_{\textrm{MO}} </math> and <math>\Psi_{\textrm{VB}} </math> .
2. Expand <math>\Psi_{\textrm{VB}} </math> into elementary determinants containing only <math>n</math> and <math>p</math> orbitals, eliminate determinants having two identical spinorbitals, and show the equivalence between <math>\Psi_{\textrm{VB}}</math> and <math>\Psi_{\textrm{MO}}</math>.
3. We now remove one electron from H<math>{}_2</math>O. Write the two possible VB structures <math>\Phi_1</math> and <math>\Phi_2</math> in the VB framework.
4. The two ionized states are the symmetry-adapted combinations 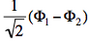and 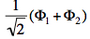. From the sign of the hamiltonian matrix element <math>\langle \Phi_1 \vert \hat{H} \vert \Phi_2 \rangle</math>, give the energy ordering of the two ionized states.
5. By expanding the two ionized states into elementary determinants (dropping the normalization constants), show that they are equivalent, respectively, to the MO configurations <math>\vert nn\bar{p}\vert</math> and <math>\vert pp\bar{n}\vert</math>.

Appendix

Hamiltonian matrix element between determinants differing by one spin-orbital :

<math>\langle \cdots i \cdots \vert \hat{H} \vert \cdots j \cdots\rangle = \beta_{ij}</math>

Don’t forget to put the orbitals of the two determinants in maximal correspondence before applying the rule.

>> Answer

Exercise 2 : Starting up with the H<math>{}_2</math> molecule

***** INPUT FILES TO BE FINALIZED *****

Two Gamess and XMVB input files for the H<math>{}_2</math> molecule are provided in the Exercise folder on the tutorial machines :

• the file h2-atom.xmi input uses the fragment specification in terms of atoms (frgtyp=atom) ;
• the file h2-sao.xmi input uses the fragment specification in terms of symmetry-adapted orbitals (frgtyp=sao).

There are VBSCF calculations with the 6-31G(d,p) basis set. Just inspect these inputs, run the gamess-xmvb program (using : vbrun h2-atom and : vbrun h2-sao, and analyze the outputs.

Then these input files could serve you as templates for the next exercises.

Before moving to the next exercises, please read the following :

>>> general guidelines for BOVB calculations

Exercise 3 : HF molecule : weights and bond energy

***** INPUT FILES TO BE FINALIZED *****

1. Compute a VBSCF three structure wave function for the HF molecule, using the frgtyp=sao specification and automatic guess (guess=auto). Which structure(s) should be kept in further BOVB calculations ?
2. Using VBSCF orbitals as guess orbitals :
   1. Compute a L-BOVB wave function on a selected subset of structures ;
   2. Compute a VBCISD wave function for the multi-structure wave function
   3. Compare structure weights at the VBSCF, L-BOVB and VBCI levels
3. Compute bond energies at the L-BOVB and VBCISD levels.

>> Hints and remarks

Exercise 4 : F<math>{}_2</math> molecule and charge-shift resonance energy

***** INPUT FILES TO BE FINALIZED *****

1. Compute a VBSCF wave function for the F<math>{}_2</math> molecule, using the cc-pvtz basis set, and with inactive orbitals localized on only one of the fluorine atoms ;
   1. first the frgtyp=sao specification and automatic guess (guess=auto) ;
   2. second the frgtyp=atom specification and providing HF MOs as guess orbital through an extra $Gus section in the xmvb input
2. BOVB level :
   1. Compute a L-BOVB wave function using VBSCF orbitals as guess orbitals ;
   2. Starting from the previous solution, compute a D-BOVB solution, by allowing only the inactive to delocalize onto the two atoms, while the active orbitals are kept frozen. Compare total energy with the previous level.
3. We want to calculate the charge-shift resonance energy (RE__CS) for the F<math>{}_2</math> molecule. For that, we have to compute a VB wave-function corresponding to a single covalent structure, and take the energy difference with the full (covalent+ionic) wave-function.
   1. Compute a purely covalent wave function for F<math>{}_2</math> at the VBSCF level. What would be the L-BOVB solution ?
   2. Compute a purely covalent wave function for F<math>{}_2</math> at the D-BOVB level.
   3. Deduce the RE__CS at the VBSCF, L-BOVB and D-BOVB. Compare its value computed at the D-BOVB level with the bond energy (Experimental : ~40 kcal/mol).

>> Hints and remarks

Exercice 5 : Solvent effect on C(Me)<math>{}_3</math>-Cl weights

***** INPUT FILES TO BE WRITTEN *****

1. C(Me)<math>{}_3</math>-Cl at equilibrium geometry :
   1. Compute a VBSCF wave function using frgtyp=atom and a $Gus section to specify guess orbitals. The active electron pair will be the C-Cl bond, and all inactive orbitals should be localized either on Cl or on the C(Me3) fragment. Which structures should be kept in further BOVB calculations ?
   2. Compute a L-BOVB wave function.
   3. Compute a D-BOVB wave function, by freezing the active orbitals, and delocalizing all inactive orbitals onto the whole molecule.
2. Starting from guess orbitals obtained at equilibrium geometry, redo the D-BOVB calculation for the large inter fragment distance. How does the weights of the different structures evolve when the molecule is stretched ?
3. Redo the D-BOVB calculations at equilibrium geometry and large distance using VBPCM for water. How does the weights change with solvation effects ?