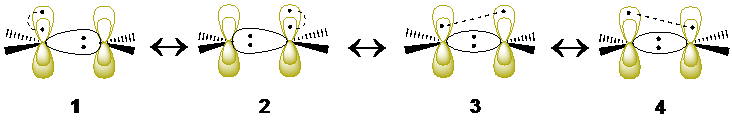Abstract pool hdr
Abstracts
Example: John Smith
University
Title
Text
[1] Popelier, P. L. A.; Brémond, É. A. G. Int.J.Quant.Chem. 2009, 109, 2542.
Henry Chermette,a Walid Lamine,a,b Christophe Morella
a Université de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France
b Université de Tunis El Manar, Faculté des Sciences de Tunis, UR11ES19 Unité de recherche Physico-Chimie des Matériaux condensés, El-Manar II, 2092, Tunis, Tunisie
Ill-advised self-interaction contribution in modeling anionic attack in a reaction path.
The catalytic role of an anion such as iodide in the insertion of CO2 into an epoxide over a Zn complex It is shown how the contribution of the iodide ion may be incorrectly modeled in a reaction path, and how the ill-advised self-interaction contribution may be approximately cured.
Philippe C. Hiberty, Wei Wu, Huaiyu Zhang, Benoît Braida, Sason Shaik
V state of ethylene: from myriads of MO-CI configurations to just four valence bond structures
The first singlet excited state of ethylene (so-called the V state) is a notoriously difficult test case that has necessitated elaborate strategies and extensive configuration interaction in the molecular orbital (MO) framework. By contrast, the description of this electronic state and its transition energy from the ground state (so-called the N state), becomes very simple with valence bond methods. It is shown that extremely compact wave functions, made of three VB structures for the N state and four structures for the V state (1-4 in the scheme below), provide an N→V transition energy of 8.01 eV, in good agreement with experiment (7.88 eV for the N→V transition energy estimated from experiments). Further improvement to 7.96/7.93 eV is achieved at the variational and diffusion Monte Carlo (MC) levels, using a Jastrow factor coupled with the same compact VB wave functions. Furthermore, the measure of the spatial extension of the V state wave function, 19.14 a02, is in the range of accepted values obtained by large-scale state-of-the-art MO-based methods. The σ response to the fluctuations of the π electrons in the V state, known to be a crucial feature of the V state, is taken into account using the breathing-orbital valence bond method (BOVB), which allows the VB structures to have different sets of orbitals, as is made apparent in 1 and 2. Further valence bond calculations in a larger space of configurations confirm the results of the minimal structure-set, yielding an N→V transition energy of 7.97 eV and a spatial extension of 19.16 a02 for the V state. Both types of valence bond calculations show that the V state of ethylene is not fully ionic as usually assumed, but involving also a symmetry-adapted combination of VB structures,3 and 4, each with asymmetric covalent π bonds. The latter VB structures have cumulated weights of at least 18-26%, and stabilize the V state by about 0.9 eV. It is further shown that these latter VB structures, rather than the commonly considered zwitterionic ones, are the ones responsible for the spatial extension of the V state, known to be ca. 50% larger than the V state.
Aurélien de la Lande
Laboratoire de Chimie Physique, Université Paris Sud, CNRS, Université Paris Saclay. 15, avenue Jean Perrin, 91405 Orsay, Cedex. France
Robust, basis-set independent method for the evaluation of charge-transfer energy in nonconvalent complexes
Separation of the energetic contribution of charge transfer to interaction energy in noncovalent complexes would provide important insight into the mechanisms of the interaction. However, the calculation of charge-transfer energy is not an easy task. It is not a physically well-defined term and the results might depend on how it is described in practice. Commonly, the charge transfer is defined in terms of molecular orbitals; in this framework, however, the charge transfer vanishes as the basis set size increases towards the complete basis set limit. This can be avoided by defining the charge transfer in terms of the spatial extent of the electron densities of the interacting molecules, but the schemes used so far do not reflect the actual electronic structure of each particular system and thus are not reliable. We propose a novel approach – spatial partitioning of the system which is based on a charge transfer-free reference state, namely superimposition of electron densities of the non-interacting fragments. We show that this method, employing constrained DFT for the calculation of the charge-transfer energy, yields reliable results and is robust with respect to the strength of the charge transfer, the basis set size and the DFT functional used. Because it is based on DFT, the method is applicable to rather large systems.
[1] Řezáč, J; de la Lande, A. J. Chem. Theor. Comput. 2015, 11, 528-537.
A. Martín Pendás
Universidad de Oviedo, Julian Claveria, 33006, Oviedo, Spain
Electron distribution functions from academic models: towards a real space Aufbau principle
Electron number distribution functions (EDFs) allow for the computation of the weights of
real space resonance structures. To obtain them we need a partition of
space into chemically meaningul regions, i.e. through QTAIM, ELF, Hirshfeld, or any other
exhaustive or fuzzy decomposition available in the literature.
With such a decomposition we may compute the probability of distributing the N electrons of a molecular system into the m regions in which we have divided space, in every possible way. EDFs provide valuable insight into chemical bonding, and here we show that they may be successfully approximated by very simple models, giving rise to an interesting interpretation of the standard Aufbau principle in real space. This is obtained from academic models of the wave functions of simple systems and a Mulliken-like condensation.