VBTutorial3

<< Return to the program

How to modify this page :

• first : log in (top right of this page) ;
• click on [edit] (far right) to edit a section of the page ;
• write your text directly in the wiki page, and click on the "Save page" button (bottom left) to save your modifications

Pictures : how to insert a picture in your text

See also this page for an introduction to the basics of the wiki syntax

State correlation diagrams

Remarks

>> Initial remarks for tutors

Exercises

Main Exercise

Exercise 1 : Computation of state correlation Diagrams for a 3 centers / 4 electrons system

• Computer exercise :

In this exercise the <math>\textrm{S}_{\textrm{N}}2</math> reaction Cl<math>{}^{-}</math> + CH3Cl -> ClCH3 + Cl<math>{}^{-}</math> will be computed in both vacuum and solution, at <math>\pi</math>-D-BOVB level. The basis set is 6-31+G*, for there is an anoin in the system. To make the computation simplified, only reactant and transition state will be computed in the exercise. It is recommended to the advanced users to draw the whole VBSCD.

Compute the Energies and Wavefunctions at Reactant and Transition State with Different Set of VB Structures

1. Write the following VB structure sets, compare and see the difference, and think about why:
   1. all structures;
   2. minimal structures for reactant;
   3. minimal structures for product.
2. Compute reactant in vacuum at <math>\pi</math>-D-BOVB level:
   1. Compute reactant at VBSCF level, with delocalized <math>\pi</math>-spaces, localized <math>\sigma</math>-space and all VB structures;
   2. Compute reactant at BOVB level, with VBSCF orbital as initial guess. The VB structures and orbital descriptions are the same as at VBSCF level.
   3. Do the same to computations with minimal structures for reactant and product.
3. Compute transition state at BOVB level in vacuum. The procedure is the same as computations for reactant.
4. Compute reactant in solution at <math>\pi</math>-D-BOVB level:
   1. Compute reactant in solution at VBSCF level, with the same orbital descriptions and VB structures in vacuum, using VBSCF orbital in vacuum as initial guess.
   2. Do the BOVB calculation for reactant in solution, using VBSCF/PCM orbitals as initial guess.
   3. Do the BOVB calculations with structures at reactant and product point.
5. Compute transition state in vacuum with the same procedure as for reactant in solution.

Analyze the Data from Above Computations at <math>\pi</math>-D-BOVB level

1. Compute the Barrier height of the <math>\textrm{S}_{\textrm{N}}2</math> reaction in both vacuum and solution. See the difference of the barrier heights, and find out the reason.
2. Compare the energies of reactant and product structures at reactant and transition state, in both vacuum and solution. What's the difference of the energies at different points? Why?
3. Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies.

• Compute VBSCD diagrams for Cl(-) + CH3Cl -> ClCH3 + Cl(-), at π-D-BOVB levels, first in gas phase then using VB(PCM)... Which basis set should we use : 6-31+G*. As this is an anion we should add a set of diffuse functions, but then there may be trouble with BOVB... Check first that everything is fine at BOVB level (no instability)...

• Reactant and product geometry will be CH3Cl and Cl(-) computed separately (CH3Cl has already been computed in tutorial 1, we just have to change the basis set, which is easy with XMVB 2.0 !) ;
• TS transition state : we take the linear TS, with orientation of the x or y axis along a C-H bond this will make a <math>\sigma</math>, <math>\pi_x</math>, <math>\pi_y</math> separation, so we could apply π-D-BOVB level, localizing all <math>\sigma</math> pairs (including inactive <math>\sigma</math> lone pairs and cores of Carbon and Chlorine atoms, and delocalizing the and <math>\pi_x</math> and <math>\pi_y</math> inactive orbitals from the beginning ((see also "high symmetry cases" here)|.

>> Answer

>> general guidelines for BOVB calculations

Exercise 2 : computation of H—H + H. -> H. + H—H radical exchange VBSCD diagram

1/ Paper exercise :

a/ Considering the following radical exchange process: <math> X^{\bullet} + A-Y \rightarrow X-A + ^{\bullet}Y </math> (X = A = Y = hydrogen atom)

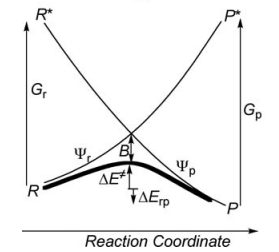
Write the HL wave functions for R and R* and derive the value of G using semiempirical VB theory. Indications : 1) neglect the overlap beween the external atoms X and Y, and neglect the overlap between two different determinants; 2) the resonance energy arising from the mixing of two degenerate VB structures is given by the following expression:

<math>RE = [H_{12}-E_{ind}S_{12}]/(1+S_{12}) </math>

where <math> E_{ind} </math> is the energy of an individual VB structure, and <math> S_{12} </math> and <math> H_{12} </math> are respectively the overlap and Hamiltonian matrix element between the two VB structures.

b/ Considering the following reaction: <math> X^{\bullet} + H-X \rightarrow X-H +^{\bullet}X </math>
Use semiempirical VB theory to derive the following expression for the avoided crossing term <math> B </math> :
<math>B = 0.25\Delta E_{ST} </math>' where <math>\Delta E_{ST} </math>' is the singlet-triplet transition energy of the X-H bond at the geometry of the transitions state.
Now it is known that for strong binders, at any given bonding distance the singlet-triplet transition energy is larger than twice the bonding energy of the dimer at equilibrium distance, so that one can write the approximate expression <math>\Delta E_{ST} </math>' <math> = 2 BDE </math>, where <math> BDE </math> is the bonding energy of the dimer at equilibrium distance. Using the latter expression, express the avoided crossing term <math> B </math> as a function of the bonding energy of <math> H_{2}</math>.

c/ Use semiempirical VB theory to show why the reaction: <math> X^{\bullet} + H-X \rightarrow X-H + ^{\bullet}X</math> has a barrier for <math>X= CH_{3}</math>, <math>SiH_{3}</math>, <math>GeH_{3}</math>, <math>SnH_{3}</math>, <math>PbH_{3}</math>, <math>H</math>, while the <math>Li_{3}</math> species in the process <math> Li^{\bullet} + Li-Li \rightarrow Li-Li + ^{\bullet}Li</math> is a stable intermediate. First construct a VBSCD with the usual parameters <math>\Delta E_{ST}, f, G, B</math>. Where <math>\Delta E_{ST}</math> is the singlet-triplet transition energy of the X-H bond at the geometry of the transition state. For convenience, define the energy of a Lewis bond, for example, H-X (or X-X), relative to the nonbonded quasiclassical reference determinant, as follows:
<math>E_{S}(H-X)=-\lambda_{S}</math> and <math>D(H-X)=\lambda_{S}</math> where <math>\lambda_{S}</math> is used as a shorthand notation for <math>2\beta S/(1+S^2)</math>. Similarly, denote the energy of the triplet pair <math>H \uparrow \uparrow X</math> (or of <math>X \uparrow \uparrow X</math>) by: <math>E_{T}(H \uparrow \uparrow X)=\lambda_{T}</math>, where <math>\lambda_{T}</math> is the corresponding <math>-2\beta S/(1-S^2)</math> terms for the triplet repulsion. While <math>\lambda_{S}</math> and <math>\lambda_{T}</math> are defined at the equilibrium distance of the H-X (or X-X) bond, analogous parameters <math>\lambda'_{S}</math> and <math>\lambda'_{T}</math> are defined for the stretched H-X (or X-X) bond corresponding to the geometry of the transition state. Based on these notations derive the following relations and quantities:
- Express <math>\Delta E_{ST}</math> and <math>G</math> as functions of <math>\lambda_{S}</math> and <math>\lambda_{T}</math>.
- Express the avoided crossing interaction <math>B</math> as a function of <math>\lambda'_{S}</math> and <math>\lambda'_{T}</math>.
- Express the energy of the crossing point (relative to the reference quasiclassical determinant) as a function of <math>\lambda'_{S}</math> and <math>\lambda'_{T}</math>.
- To enable yourself to derive a simple expression for the barrier, assume that <math>\lambda'_{S}=\lambda'_{T}</math>. Then express <math>\Delta E_{C}</math>, the height of the crossing point relative to the reactants, and derive an expression for <math>f</math>, as a function of <math>\alpha</math>, defined as follows: <math>\alpha=\lambda_{S}/\lambda_{T}</math>.
- Derive an expression for the barrier <math>\Delta E^{\neq}</math>, as a function of <math>\Delta E_{ST}</math> and <math>\alpha</math>. Knowing that <math>\lambda_{T}</math> is generally larger than <math>\lambda_{S}</math> for strong binders, such as X-H (<math>X= CH_{3}</math>, <math>SiH_{3}</math>, <math>GeH_{3}</math>, <math>SnH_{3}</math>, <math>PbH_{3}</math>, <math>H</math>) while the opposite is true for weak binders, such as alkali atoms, show that the reaction <math>X^{\bullet} + H-X \rightarrow X-H + ^{\bullet}X</math> has a barrier while the <math>Li_{3}</math> species is a stable intermediate in the process <math> Li^{\bullet} + Li-Li \rightarrow Li-Li + ^{\bullet}Li</math>.

2/ Computer exercise :VBSCD for H—H + H. -> H. + H—H at VBSCF then VBCISD level.

In this exercise the VBSCD for H—H + H. -> H. + H—H at VBSCF then VBCISD level will be computed with 6-31G**. Computations for reactant and transition state are requested and other points are optional for advanced users.

Compute the Energies and Wavefunctions at Reactant and Transition State with Different Set of VB Structures

1. Write the following VB structure sets, compare and see the difference, and think about why:
   1. all structures;
   2. minimal structures for reactant;
   3. minimal structures for product.
2. Compute reactant at VBSCF and VBCISD level:
   1. Compute reactant at VBSCF level with "orbtyp=hao" and "boys";
   2. Compute reactant at VBCISD level, with VBSCF orbital as initial guess.
   3. Do the same to computations with minimal structures for reactant and product point.
3. Compute transition state at VBCISD level with the same procedure as for reactant.

Analyze the Data from Above Computations at VBSCF and VBCISD levels

1. Compute the Barrier height of the <math>\textrm{S}_{\textrm{N}}2</math> reaction at VBSCF and VBCISD levels. See the difference of the barrier heights.
2. Compare the energies for reactant and product structures at reactant and transition state, by both VBSCF and VBCISD. What's the difference of the energies at different points? Why?
3. Compute the resonance energies at both reactant and transition state points, see the difference of the resonance energies.

Optional: Compute all points and draw the VBSCDs at VBSCF and VBCISD levels.

>> Answer

Exercise 3 (paper exercise) : Conical intersection in H₃^• radical

(for further reading, see S. Shaik and P.C. Hiberty, "The Chemist's Guide to VB theory", Wiley, Hoboken, New Jersey, 2008, pp. 157-161, exercises 6.11-6.14 pp. 174-176, and answers to the exercises pp. 188-192.

Consider three hydrogen atoms Ha, Hb, Hc, with respective atomic orbitals a, b and c, and the two VB structures ] and ] .

The Ha-Hb and Hb-Hc distances are equal.

1. By using the thumb rules recalled below, where squared overlap terms are neglected, derive the expression of the energies of R and P, and of the reduced Hamiltonian matrix element between R and P for the 3-orbital/3-electrons reacting system [Ha--Hb--Hc]•.
2. From the sign of this latter integral when θ > 60°, derive the expressions of the ground state Ψ^≠ and of the first excited state Ψ* of the H₃• system. One may drop the normalization constants for simplicity. What bonding scheme does the excited state represent ?
3. Show that the reduced Hamiltonian matrix element is largest in the collinear transition state geometry, and drops to zero in the equilateral triangular structure.
4. Show that R and P VB structures are degenerate in the equilateral triangular structure, and that Ψ≠ and Ψ* are also degenerate in this geometry.
5. We now extend the above conclusions to the allyl radical. What are the bonding schemes corresponding to the ground state and first excited state ? What geometrical distortion would make these two states degenerate ? What would be the end product of a photochemical excitation of allyl radical to its first excited state ?

Appendix : Thumb rules for the calculations of effective Hamiltonian matrix elements between determinants.

1. Energy of a determinant D : ] (if orbitals i and j have parallel spins)
2. Matrix element between determinants differing by spin inversion of two spin-orbitals :]

>> Answer