General guidelines for BOVB calculations

Active space

First, choose an active system of orbitals/electrons in the molecule under study. This is the part of the molecule that will be treated in a VB way : for example the bonds that are made/broken in a reaction, or the orbitals whose occupancy varies in a series of resonating VB structures. The occupancies of the active orbitals will change from one VB structure to the other. The other orbitals, called « inactive » or « spectator », are those that keep the same occupancy in all VB structures.

Selection of structures

BOVB calculations should be carried out only on a selected subset of the most chemically meaningful structures. If the total number of possible VB structures^* is not very large (<100), the best option is to run first a VB calculation using the str=full option (which will generate the full basis of VB structures), and then select for the subsequent VB calculation the structures which have a weight superior to ~1%. If the total number of possible structure is very large, then a selection of structures at the VBSCF based on chemical ground should be done first.

* To calculate what is the total number of structures you can use the Weyl formula, see slide 12 in Philippe Hiberty's second lecture

BOVB levels

Each active orbital must be defined as localized, either on a single atom or on a fragment (recommended, see next section below). The inactive orbitals may be kept localized (L-VBSCF or L-BOVB) or allowed to delocalize on the whole molecule (D-VBSCF or D-BOVB). Better accuracy is obtained in this latter case. Last, in the ionic structures the doubly occupied active orbitals may be "splitted" for a better description, leading to the S-BOVB (if inactive are kept localized) and SD-BOVB levels.

Recommended definition for the orbital blocks

These rules lead to the definition of "orbital blocks" :

From your active orbitals divide the molecule into fragments, such as two active orbitals involved in a covalent coupling in one of the structures belong to different fragments;
To each fragment is associated a localization space : the orbitals belonging to a specific localization space can only span the basis functions centered on atoms belonging to this fragment;
The different localization spaces may then be further divided according to the symmetry of the molecule (<math>\sigma</math>/<math>\pi</math> separation for instance), which provides the different orbital blocks.

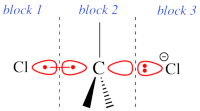
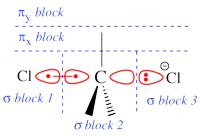
Two example choices of orbital blocks definitions for Cl-(Me₃)C-Cl^- SN2 linear transition state geometry. Note that the r.h.s. choice corresponds to the so-called π-D-VBSCF and π-D-BOVB levels (see also example 2 below). This is the recommended option in cases where a <math>\sigma</math> / <math>\pi</math> separation is present.

Remarks :
within this definition all orbitals will be fragment orbitals, and both active/inactives orbitals belonging to the same orbital block will share the same definition in terms of basis function expansion ; if this definition is strictly followed, there is no common basis functions between orbital blocks ; orbital blocks belonging to different localization spaces and containing only inactive orbitals can be grouped together (see example 2 below) Of course, it is not always reasonable to strictly follow this definition for orbital blocks, as it cause in some cases some important physical interactions described by some inactive orbitals to be broken (for instance, if it leads to break a bond described by an inactive MO). In such cases, you may need to define different orbital blocks for inactive and active orbitals which will share some basis functions in common. This might lead in some cases to convergence issues or instabilities (orbital flipping for instance).

Exemples :
for the F₂ molecule, six blocks can be defined : <math>\sigma</math>(F₁), <math>\pi_{x}</math>(F₁), <math>\pi_{y}</math>(F₁), <math>\sigma</math>(F₂), <math>\pi_{x}</math>(F₂), <math>\pi_{y}</math>(F₂) However, if the <math>\sigma</math> bond is taken as the active electron pair, four blocks could as well be used from the beginning : <math>\sigma</math>(F₁), <math>\sigma</math>(F₂), <math>\pi_{x}</math>(F₁-F₂), <math>\pi_{y}</math>(F₁-F₂). Then, you can choose to keep the <math>\sigma</math> lone pairs localized all along the calculation (as its delocalization brings very minor energy lowering), this level has been referred to as π-D-VBSCF and π-D-BOVB ; for the (Me₃)C-Cl molecule, where we choose the C-Cl bond to be the active electron pair, the inactive orbitals are defined on the (Me₃)C and Cl fragments respectively for Cl-(Me₃)C-Cl^- SN2 transition state, the two Cl-C and C-Cl bonds are chosen as active pairs, which in turns define three fragments : Cl₁ / (Me₃)C / Cl₂

Procedure for doing a D-BOVB calculation

General case (low symmetry):

Perform a ("L") VBSCF calculation together with the keyword boys in the $orb section ;
perform the L-BOVB calculation, always starting from converged VBSCF orbitals ;
then perform the D-BOVB calculation : starting from the converged L-BOVB orbital as guess, delocalize all inactive orbitals, and run the calculation by optimizing the delocalized inactive orbitals while freezing the active orbitals during the optimization (put "0" as coefficient in first $orb line).

High symmetry case:

This is even simpler. This case is encoutered when the inactive orbitals that we wish to delocalize can be distinguished from the active orbitals by symmetry. Example : we wish to delocalize the inactive π orbitals of F2, while the active orbitals are of σ type. In such a case, one may let the VBSCF wave function converge directly in a single step (called D-VBSCF), by defining the π orbitals as delocalized, and the active orbitals and remaining inactive orbitals as localized with σ symmetry. Note that in this case the σ inactive lone pairs of F2 will not be delocalized. Since the delocalization of inactive orbital is not complete, we may refer this calculation as π-D-VBSCF. The π-D-BOVB is got the same way, taking the as D-VBSCF as a guess. We recommend this choice whenever possible. See also the picture above for an illustration of the π-D-BOVB method on the Cl-(Me₃)C-Cl^- SN2 linear transition state.

Remark :
In the particular case where all orbital blocks contain only either active or inactive orbitals, all blocks containing inactive orbitals could be grouped into a single one, and then one works at the "D" level from the start (D-VBSCF, then D-BOVB calculation). This is the case for instance when there is a <math>\sigma</math>/<math>\pi</math> separation in your molecule with all (and only) <math>\pi</math> pairs taken as active (see tutorial 2 exercises).

>>> SD-BOVB calculations (expert level)

Computing bond energies

Note that the (π-)D-BOVB wave function dissociation limit corresponds to the individual fragments computed separately at the R(O)HF level. So computation of bond energies requires a D-BOVB calculation for the molecule at equilibrium distances only, and two R(O)HF calculations for the separate fragments.

General advices

Do not use diffuse functions unless you deal with an anion, and do not use larger than triple-zeta basis sets
Impose a high molecular symmetry if possible (case of a distorted molecule which slightly departs from a higher symmetry point group) ;
Discard from your BOVB wave functions all structures which have a small weight at the VBSCF level (Coulson-Chirgwin weight of ≈1% or less) ;
Use orbtyp=hao together with fragtyp=sao specification (fragtyp=atom is not recommended for BOVB calculations), and use all the possible (pseudo-)symmetry you have in your system ;
In the $ctrl section of the XMVB input, you should use the "iscf=5" algorithm for VBSCF calculations, and change it to "iscf=2" for BOVB calculations.
Use the boys keyword at the VBSCF step, as it provides more physically meaningful orbitals for the subsequent BOVB calculations (this is particularly important if you want to go up to the S- or SD-BOVB levels)
Always use a set of converged orbitals from the preceding step, ex : use converged VBSCF orbitals to start a L-BOVB calculation, converged L-BOVB to start a S-BOVB or a D-BOVB calculation, and converged S-BOVB orbitals to start a SD-BOVB calculation.

Convergence issues
Sometimes, BOVB calculations are subject to instabilities that it is important to detect. They may manifest as incredibly high bonding energies, generally associated with strongly negative weights of the VB structures according to the Coulson-Chirgwin definition. Then, how I know whether or not my BOVB calculation went well ? Check the following quantities : The BOVB weights should not change dramatically as compared with VBSCF weights (not more than +/- ~5%) ; large negative weights (<-0.05) Coulson-Chirgwin weights are also a sign of convergence on an unphysical solution ; the overlap matrix between 2 given structures should not exceed ~0.7 the total energy : when an instability occur, it may become too low, leading to, for instance, dissociation energies which might be (sometimes significantly) larger than exact ones ; the orbital overlap (in the ".xdat" file) between active orbitals : corresponding active orbitals in different structures should have almost 1. overlap (~0.98/0.99x). When it is not the case : inspect the corresponding orbital to check what it has become What can I do if I encounter an instability or convergence issue ? Check the following points : Did I use a non-redundant description, and in particular did I kept my active orbitals all strictly localized ? Did I ask for boys localization at the initial VBSCF step ? Did I start the different steps of BOVB calculations from orbital properly converged from the previous step ? Did I eliminate all structures which have shown to be negligible (≈1% weight or less) at the VBSCF level in the subsequent BOVB calculation ? Did I use a basis set with diffuse functions, or a basis set larger than triple-zeta (which could cause trouble) ? Generally speaking : did I precisely follow the guidelines and procedure described above ? How to cure the problem - if I haven't done any particular "mistake" : try, if possible, to work in a higher symmetry point group for your molecule ; try to restart from the VBSCF level with another orbital guess (localized MOs for instance) ; try to modify slightly the definition of the wave-function, and proceed step-by-step : in a first VBSCF step : localize further the inactive orbitals if possible, and use active orbitals localized on one atom instead of a fragment. Together with the boys option, this step should generate clean and physically meaningful orbitals ; then, in a second VBSCF step : delocalize your active/inactive orbitals onto fragments, using as closely as possible the above recommendation for the definition of your orbital blocks. try to work in a different basis set.