Abstract pool for the NCI workshop
<<< Topological Approaches to Intermolecular Interactions workshop main page
You can add your abstract below:
- first : log in;
- click on "edit", on the righthand corner above the the line below "Your name"
- copy the example given (also available >>> here) and paste it at the end of this page
- fill in the fields with your data
- >>> How to insert a picture in your abstract
- Don't forget to send us an email with the type of contribution you would like to make
Mauro Causà
Deparment of Chemical and Materials Engineering, Universita' di Napoli "Federico II"
Maximum Probability Domains in molecular crystals and surfaces
The Maximum Probability Domain (MPD) analysis due to Andreas Savin is applyed to molecular crystals and their surfaces. The correlation effects are included using Quantum Monte Carlo techniques. The MPD correlated method will be applied to rare gas solids, organic materials applied in photo-electronics, and to crystal phases relevant in heterogeneous atmospheric chemistry.
Piotr Kasprzycki
Institute of Experimental Physics, Faculty of Physics, University of Warsaw, ul. Hoza 69, 00-681 Warsaw, Poland
The correlation between the proton transfer time and electron density in the inner cavity of porphycenes
Numerical solutions of the Schrödinger equation can nowadays be obtained for reasonably large organic and organometallic molecules with useful accuracy using approximate ab initio or DFT methods. These approximate solutions are also available for porphycene which is an important chromophore [1]. Porphycene and its derivatives show useful properties for material sciences and are also considered excellent photosensitive media for applications in photodynamical therapy of cancer [2]. Several papers have discussed the energy structure and dynamic aspects of hydrogen transfer in this systems [4, 5]. We report on the results of NCI analysis - theoretical tool based on Bader approach [6] - performed for symmetrically and asymmetrically substituted porphycene derivatives. We have carried out DFT calculations at the level B3LYP/6-311(d,p) of theory. These calculations were followed by NCI analysis. Calculations showed a correlation between the value of electron density gradient localized between nitrogen and hydrogen atoms in the inner cavity of a molecule and the time of the proton transfer in the examined systems. Proton transfer times were obtained in a femtosecond transient absorption anisotropy experiment, which is a polarisation-sensitive variant of an ultrafast pump-probe technique. Double hydrogen transfer leads to the change of transition dipole moment directions - transition moment of chemically identical tautomerization product forms an angle of α = (72±2)◦ with that of initially excited form. This change is manifested as variation in transmitted light intensity measured in two orthogonal polarizations. Under appropriate conditions, rise/decay times of anisotropy reflect the kinetics of double hydrogen transfer. We show that quantum theory of atoms in molecules (QTAIM) based on Bader approach is useful not only for detection of covalent bond but also for hydrogen bonds and weak van der Waals interaction. NCI analysis provides the possibility to compare strength of hydrogen bonds in porphycene derivatives, which allows one to predict the proton transfer time for new molecules. Additionally, these approach have helped us to design structure of a derivative with the proton transfer time of the order of tens of picoseconds. Furthermore, substitution in 2,7 and in 10,19 position of porphycene can induce differentiation of hydrogen bonds. The effect is especially evident in the case of 10,19-di-methylporphycene (2MPc) and 2,7-di-t-buthylporphycene (DTBP). This behavior may be the result of asymmetric distribution of electron density in the center of the molecule. This fact can be significant for understanding the mechanism of double hydrogen transfer between inner nitrogen atoms.
References
[1] D. Sanchez-Garcia, J. L. Sessler, Chem. Soc. Rev., 37, 215, (2008). [2] J. C. Stockert, M. Canete, A. Juarranz, A. Villanueva, R. W. Horobin, J. I. Borrell, J. Teixido, S. Nonell, Curr. Med. Chem., 14, 997, (2007) . [4] Ł. Walewski, J. Waluk, B. Lesyng, J. Phys. Chem. A., 114, 2313–2318, (2010). [5] M. Gil, J. Waluk J. Am. Chem. Soc. 5, 129, (2007). [6] E. R. Johnson, S. Keinan, , J. Contreras-García, R. Chaudret, J-P Piquemal, D. Beratant, W. Yang, J. Chem. Theo. and Comp., 25, (2011).
Slawomir J. Grabowski
Faculty of Chemistry, University of the Basque Country UPV/EHU, and Donostia International Physics Center (DIPC),P.K. 1072, 20080 Donostia, Spain IKERBASQUE, Basque Foundation for Science, 48011 Bilbao, Spain
Non-covalent interactions: characteristics and mechanisms of formation - the topological approach
Numerous non-covalent interactions are characterized by the electron charge transfer from the Lewis base unit to the Lewis acid [1]. This is connected with the other processes reflected by the change of geometrical, energetic and topological parameters. For example, different characteristics of the hydrogen bond and various criteria of the existence of this interaction were discussed in the literature [2]. One can mention the topological criteria of Koch and Popelier [3,4]. On the other hand, the hydrogen bond mechanism was discussed in terms of NBO method [5]. Very recently it was found that the hydrogen bond, the halogen bond and other non-covalent interactions are steered by the same processes [6]. This is reflected by the same changes of parameters. For example, the A-H...B hydrogen bond formation is connected with the increase of the positive charge of H-atom and the decrease of its volume. The same changes are observed for X-halogen atom in the A-X...B halogen bond. Various similarities and differences between numerous non-covalent interactions may be discussed.
References
[1] Lipkowski, P.; Grabowski, S. J.; Leszczynski, J. J. Phys. Chem. A 2006, 110, 10296–10302. [2] Grabowski, S.J. Chem.Rev. 2011, 11, 2597-2625. [3] Koch, U.; Popelier, P.L.A. J.Phys.Chem. 1995, 99, 9747-9754. [4] Popelier, P. Atoms in Molecules. An Introduction, Prentice Hall, Pearson Education Limited 2000. [5] Alabugin, I.V.; Manoharan, M.; Peabody, S.; Weinhold, F. J.Am.Chem.Soc. 2003, 125, 5973-5987. [6] Grabowski, S.J. Phys.Chem.Chem.Phys. accepted
Vincent Tognetti and Laurent Joubert
Normandy Univ., COBRA UMR 6014 & FR 3038, Mont Saint Aignan, 76821 cedex, France
QTAIM/DFT descriptors for the description of “weak” interactions
We present here part of our recent work, which aims to design new molecular and atomic descriptors by building a bridge between Density Functional Theory (DFT) and Bader’s Atomsin- molecules (AIM) theory,1 two frameworks that share the same primary ingredient: the electron density. A local point of view will first be presented, dealing with the so-called bond critical points (BCPs). New BCP properties will be investigated,2,3,4,5 based on reduced density gradients and on the variations rates of kinetic, exchange and correlation density energies. Interestingly, these quantities reveal particularly suited to the description of weak interactions, like hydrogen or agostic bonds. Then, we will discuss,6 using Pendás’ Interacting Quantum Atoms scheme,7 to what extent the existence or the absence of such BCPs can be rationalized in terms of integrated interatomic energies, enlightening the fundamental role of exchange channels.8 We will consequently present a fast and accurate protocol for the evaluation of the exchange interaction between two atoms,9 making another promising step in the pathway linking DFT and AIM.
References
[1] R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press (1994). [1] V. Tognetti, L. Joubert, P. Cortona and C. Adamo, J. Phys. Chem. A 113 12322-12327 (2009). [3] V. Tognetti, L. Joubert and C. Adamo, J. Chem. Phys. 132 211101 (2010). [4] V. Tognetti and L. Joubert, J. Phys. Chem. A 115 5505-5515 (2011). [5] V. Tognetti, L. Joubert, R. Raucoules, T. De Bruin and C. Adamo, J. Phys. Chem. A 116 5472-5479 (2012). [6] V. Tognetti and L. Joubert, J. Chem. Phys. 138 024102 (2013). [7] M. A Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput. 1 1096-1109 (2005). [8] A. Martín Pendás, E. Francisco, M. A. Blanco and C. Gatti, Chem. Eur. J. 13 9362-9371 (2007). [9] V. Tognetti and L. Joubert, in preparation.
Agnieszka Roztoczyńska, Justyna Kozłowska, Paweł Lipkowski, Wojciech Bartkowiak
Theoretical Chemistry Group, Institute of Physical and Theoretical Chemistry, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 53-370, Wrocław, Poland
Influence of spatial confinement on the cooperativity in the hydrogen-bonded clusters
Cooperativity is a well-known phenomenon and a steering factor of many chemical and physical properties of molecular matter [1-5]. In the present contribution the influence of chemical compression on the hydrogen bond cooperativity has been investigated. For that purpose the cooperativity effects in the isolated and confined (HF)n and (HCN)n clusters were considered. Two models of spatial confinement have been applied in our study. The first one is the cylindrical model harmonic potential, which certainly reflects the general aspects of the confinement effect. The second, less simplified model based on the supermolecular approach: molecular cages within which one can distinguish helium and carbon nanotubes. In order to get an insight into the nature of the cooperative effects in confined spaces a detailed analysis of the energetics and the topological features of electron density according to the concept of the “Quantum Theory of Atoms in Molecules” (QTAIM) proposed by Bader [6,7] have been performed. The properties in question have been analyzed using the ONIOM (M06-2X/6-311++G(2df,2pd):M06-2X/6-31G(d)) method. Moreover, in the case of the harmonic potential calculations, the second-order Møller-Plesset perturbation theory (MP2) has been applied as well. As a part of the study, the comparison of the data obtained within different models of orbital compression have been performed in order to establish the correspondence between the chemical environment and its approximate representations.
[1] A. Korpfen, J. Phys. Chem. 100, 13474 (1996).
[2] T. Kar, S. Scheiner, J. Phys. Chem. A 108, 91619168 (2004).
[3] M. Ziółkowski, S. J. Grabowski, J. Leszczyński, J. Phys. Chem. A 110, 65146521 (2006).
[4] H.J. Song, H.M. Xiao, H.S. Dong, J. Chem. Phys. 125, 074308 (2006).
[5] S. J. Grabowski, Theor. Chem. Acc. 132, 1347 (2013).
[6] R. F. W. Bader, Atoms In Molecules, A Quantum Theory; Oxford University Press: Oxford, U.K., 1990.
[7] R. F. W. Bader, Chem. Rev. 91, 893 (1991).
Paweł Lipkowski, Justyna Kozłowska, Agnieszka Roztoczyńska, Wojciech Bartkowiak
Theoretical Chemistry Group, Institute of Physical and Theoretical Chemistry, Wrocław University of Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
Behavior of model hydrogen bonded complexes under the influence of external pressure
Despite of the numerous theoretical and experimental investigations concerning the hydrogen bond phenomenon as well as to the confinement effect there is still a small number of reports on the behavior of the H-bonded systems in the presence of external pressure [1-4]. In order to render the influence of pressure one can apply a model confining potentials which allows to describe the pure valence repulsion contribution. In the present study we have investigated the influence of external pressure, represented by the cylindrical harmonic potential V_conf=1/2(x^2+y^2)ω^2, on the selected linear hydrogen bonded complexes. The model dimeric systems: HF…HF, HCN…HCN, HCN…HCCH have been chosen as a case study. All calculations have been performed employing B3LYP, M06-2X and MP2 methods together with the 6-311++G(2df,2pd) basis set. Moreover, the varied external pressure has been controlled by the oscillator strength (ω=0.0-0.8). The studied complexes have been oriented along the z-axis of the Cartesian coordinate system and fully optimized in the presence of the two-dimensional harmonic oscillator potential. A detailed analysis of changes in topological parameters of hydrogen bonds resulting from the orbital compression has been performed according to the concept of the “Quantum Theory of Atoms in Molecules” (QTAIM) proposed by Bader [5,6]. Furthermore, an energetic analysis has shown a different manner of the interaction energy in the studied H-bonded complexes.
[1] W. Wang, D. Wang, Y. Zhang, B. Ji, A. Tion, J. Chem. Phys. 134 (2011) 054317.
[2] M.C. Gordillo, J. Marti, Chem. Phys. Lett. 329 (2000) 341.
[3] M. Jabłoński, M. Solà, J. Phys. Chem. A 114 (2010) 10253.
[4] G. Miño, R. Contreras, Chem. Phys. Lett. 486 (2010) 119.
[5] R. F. W. Bader, Atoms In Molecules, A Quantum Theory; Oxford University Press: Oxford, U.K., 1990.
[6] R.F. Bader, Chem. Rev. 91 (1991) 893.
Daniela Josa
Centro de Investigación en Química Biolóxica e Materiais Moleculares (CIQUS), Universidade de Santiago de Compostela, Rúa Jenaro de Fuente, s/n, Santiago de Compostela, 15782, Spain
A DFT-D study of stacking interactions between buckybowls and fullerenes
The first strong evidence of π···π interactions between corannulene and C60 was published in 2007, when Sygula and co-workers synthesized the molecular tweezers made up two units of corannulene that can trap one fullerene (Figure 1) [1]. Since then, the interest by concave-convex π···π interactions has been revived. The modification of the tweezers by a different functionalization of buckybowls, which constitute the main part of tweezers, could improve their efficiency and selectivity. Therefore, the aim of this work is to carry out a detailed study of the effects that can enhance the stacking interactions between buckybowls and fullerenes to achieve our ultimate goal that is predict how to modify the molecular tweezers to improve their efficiency and selectivity. All complexes studied were optimized at the B97-D/TZVP level using resolution of identity approximation (RI) implemented in TURBOMOLE 5.10 program suite [2]. Counterpoise corrections were applied to all reported interaction energies [3].
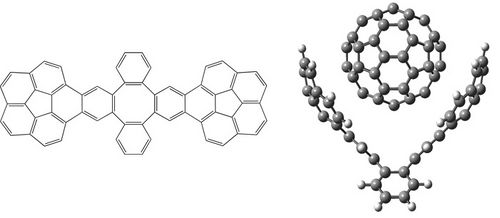
References
[1] A. Sygula, F.R. Fronczek, R. Sygula, P. W. Rabideau, M. M. Olmstead. J. Am. Chem. Soc. 2007, 129, 3842-3843.
[2] R. Ahlrichs, M. Bär, M. Häser, H. Horn, C. Kölmel. Chem. Phys. Lett. 1989, 162, 165-169.
[3] S.F. Boys, F. Bernardi. Mol Phys. 1970, 19, 553-566.
A. Martín Pendás
Universidad de Oviedo. Spain
Decay rate of delocalization indices: towards a real space image of the insulating or metallic character of a material
Real space theories of the chemical bond have come of age, and are now grouped together under the umbrella name of Quantum Chemical Topology (QCT) [1], as originally proposed by Paul Popelier. Most of what is known in chemical bonding has been successfully reformulated using QCT techniques, that provide a wealth of quantities which are invariant under general orbital transformations. However, there is still no clear indication of what type of real space quantities, if any, might be used to discriminate between metals and insulators, in spite of several initial proposals, like those of Gatti and Silvi, or Contreras et. al. Recently, Baranov and Kohout have proposed that localization or delocalization indices might hold the clue [4]. However, their unrestricted Kohn-Sham approach is not devoid of possible criticisms. Here we address the problem from a molecular point of view, examining the analytic behavior of localization and delocalization indices in analytically solvable models and pointing towards the rate of decay of these quantities as a possible measure of long-range (metallic-like) or short-range (insulating-like) electron delocalization in materials [5].
[1] Paul L. A. Popelier, Struct. Bond. 2005, 115, 1.
[2] B. Silvi, C. Gatti, J. Phys. Chem. A, 2000, 104.
[3] J. Contreras-García, A. Martín Pendás, J. M. Recio, B. Silvi , J. Chem. Theory Comput. , 2009, 5, 164.
[4] A. Baranov, M. Kohout, Acta Cryst. A 2011, 67, C115.
[5] A. Martín Pendás, in preparation.
Olga Syzgantseva, Vincent Tognetti, Laurent Joubert
UMR CNRS 6014 & FR 3038, Université de Rouen et INSA de Rouen
Analysis of halogen bonding using topological indexes and IQA energy decomposition scheme
Halogen bonding is a directional interaction occurring between a halogen and an electronegative atom of a Lewis base. It is namely responsible for ligand binding and molecular folding in biological systems and is of importance in crystal engineering [1,2]. While predominantly electrostatic character of this interaction seems to be established [3], the influence of chemical environment on its strength is not completely understood. In the present study we use topological indexes and an interacting quantum atoms (IQA) energy decomposition scheme [4] to explain how primary and secondary interactions affect the strength of a halogen bond. For this purpose, we use a series of model complexes described within DFT applying a dispersion correction. IQA energy decomposition scheme allows to extract pairwise interatomic contributions from total intermolecular interaction energy between halogen-bonded complex moieties and to estimate the proportion between Coulomb and exchange contributions [5]. Besides, the Source Function [6] analysis complements the description of the impact of chemical surroundings on the formation of halogen bond.
[1] P. Auffinger, F.A. Hays, E. Westhof, S. Ho, Proc. Nat. Acad. Sci, 2004, 101, 16789 – 16794
[2] P. Metrangolo, F. Meyer, T. Pilati, G. Resnati, G. Terraneo, Angew. Chem. Int. Ed., 2008, 47, 6114 – 6127
[3] P. Politzer, K.E. Riley, F.A. Bulat, J.S. Murray, Comp. Theor. Chem., 2012, 998, 2–8
[4] M. A. Blanco, A. Martín Pendás, E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096 – 1109
[5] O.A. Syzgantseva, V. Tognetti, L. Joubert, in preparation
[6] R.F.W. Bader, C.Gatti, Chem. Phys. Lett., 1998, 287, 233 – 238
Add your name here
This is your affiliation
This is your title
Your abstract
Frank De Proft
Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, B-1050 Brussels, Belgium
Combined use of DFT based Reactivity Indices and the Non-covalent Index in the Study of Intermolecular Interactions
Conceptual Density Functional Theory (sometimes also called DFT based reactivity theory or Chemical DFT) has proven to be an ideal framework for the introduction of chemical reactivity descriptors.[1] These indices are defined as response functions of the energy E of the system with respect to either the number of electrons N, the external potential v(r) or both. These definitions have afforded their non-empirical calculation and applications in many fields of chemistry have been performed, often combined with principles such as the electronegativity equalization principle of Sanderson and Pearson’s hard and soft acids and bases (HSAB) and maximum hardness principles. In this talk, we focus on recent studies in which a combined use of these reactivity indices and the Non-Covalent Interaction (NCI) Index[2] was carried out in order to scrutinize intermolecular interactions. In a first part, we focus on halogen bonding. Halogen bonds between the trifluoromethyl halides CF3Cl, CF3Br and CF3I, and dimethyl ether, dimethyl sulfide, trimethylamine and trimethyl phosphine were investigated using the HSAB concept with conceptual DFT reactivity indices, the Ziegler-Rauk type energy decomposition analysis,[3] the Natural Orbital for Chemical Valence framework (NOCV),[4] and the NCI index. It is found that the relative importance of electrostatic and orbital (charge transfer) interactions in these halogen bonded complexes varies as a function of both the donor and acceptor molecules.[5] Hard and soft interactions were distinguished and characterized by atomic charges, electrophilicity and local softness indices. Dual descriptor plots indicate an orbital σ-hole on the halogen similar to the electrostatic σ-hole manifested in the molecular electrostatic potential. The characteristic signal found in the reduced density gradient versus electron density diagram corresponds to the non-covalent interaction between contact atoms in the NCI plots, which is the manifestation of halogen bonding within the NCI theory. The unexpected C–X bond strengthening observed in several cases was rationalized within the MO framework.
In a second part of the talk, we present recent results on the use of the above mentioned quantities in the study of metal-metal interactions.[6]
References
[1] (a) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989. (b) R. G. Parr and W. Yang, Ann. Rev. Phys. Chem. 46, 701 (1995). (c) H. Chermette, J. Comput. Chem. 20, 129 (1999). (d) P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev. 103, 1793 (2003). (e) P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quant. Chem. 101, 520 (2005).
[2] (a) E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, Journal of the American Chemical Society 132, 6498 (2010). (b) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theor. Comput. 7, 625 (2011).
[3] (a) F. M. Bickelhaupt and E. J. Baerends, Reviews in Computational Chemistry, 15, 1 (2000); (b) T. Ziegler and A. Rauk, Theoretica Chimica Acta 46, 1 (1977).
[4] M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theor. Comput. 5, 962 (2009).
[5] B. Pinter, N. Nagels, W. A. Herrebout and F. De Proft, Chem. Eur. J. 19, 518 (2013).
[6] B. Pinter, L. Broeckaert, J. Turek, A. Růžička and F. De Proft, in preparation.
Add your name here
This is your affiliation
This is your title
Your abstract
Mercedes Alonso, Paul Geerlings and Frank De Proft
Department of General Chemistry (ALGC), Free University of Brussels (VUB), Pleinlaan 2, Brussels, 1050, Belgium
Fine-tuning of the conformation of expanded porphyrins using conceptual DFT descriptors and non-covalent index
Density functional theory (DFT) is a powerful tool to examine a broad variety of structures and reactions involving increasingly larger molecules. Moreover, it is a well-suited theory for the introduction of chemical concepts, also known as reactivity indices.[1] Recently, we have shown that DFT calculations in combination with NCI analysis[2] are very useful in aiding the design of viable Möbius aromatic systems and molecular switches of expanded porphyrins.[3-5] These macrocycles can adopt a variety of intriguing structures, with Hückel, Möbius and twisted-Hückel topologies, which can be interconverted under certain conditions. The vast structural diversity exhibited by expanded porphyrins has led to diverse applications such as non-linear optical materials and molecular sensors, although the control of molecular topology is crucial for most of applications.
Conformational preferences and interconversion pathways in penta-, hexa- and heptaphyrins have been investigated using different hybrid functionals. The stability of Hückel and Möbius conformers depends on intramolecular hydrogen bonding, ring strain, aromaticity and steric effects of the meso-substituents. We proposed a set of descriptors to quantify independently the contribution of the different factors.[3] Two torsional parameters are used to quantify ring strain. Aromaticity has been quantified using energetic, structural, magnetic and reactivity criteria. Importantly, the relative hardness (a conceptual DFT descriptor) is found to be a good descriptor of the macrocyclic aromaticity in Hückel and Möbius porphyrinoids, whereas the dual descriptor is highly useful in predicting reactivity. Steric effects of the substituents are analysed in terms of the non-covalent interaction index (NCI). NCI is capable of distinguishing intramolecular hydrogen bonds, π- π interactions, CH···π and repulsive steric clashes, based on the peaks that appear in the reduced density gradient at low densities. While the relative stabilities of [4n + 2] expanded porphyrins are mainly governed by ring strain, intramolecular hydrogen-bonding and steric effects controls the stability of [4n] congeners. Appealingly, conformational control of pentaphyrins can be achieved by changing the type and number of meso-substituents.[5]
References
[1] P. Geerlings and F. De Proft, and W. Langenaeker, Chem. Rev. 103, 1793 (2003).
[2] E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang J. Am. Chem. Soc. 132 6498-6506 (2010).
[3] M. Alonso, P. Geerlings, and F. De Proft, Chem. Eur. J. 18 10916-10928 (2012).
[4] M. Alonso, P. Geerlings, and F. De Proft, Chem. Eur. J. 19 1617-1628 (2013).
[5] M. Alonso, P. Geerlings, and F. De Proft, J. Org. Chem. accepted. DOI: 10.1021/jo4003823.
Add your name here
This is your affiliation
This is your title
Your abstract
Add your name here
This is your affiliation
This is your title
Your abstract
Add your name here
This is your affiliation
This is your title
Your abstract
Add your name here
This is your affiliation
This is your title
Your abstract
Add your name here
This is your affiliation
This is your title
Your abstract