BLW

return to Tutorial n°4

BLW - must know

The BLW program is provided by Yirong Mo (Western Michigan University - USA). It allows to optimize local wave function. Gradients are available for geometry optimization. DFT approaches allow to include a part of correlation into the structure.

The BLW input is that of Gamess supplemented by two groups to define the localization of the electrons.

$BLW group (requires $BLWDAT group)

BLW refers to the Block-Localized Wave function (BLW) method, which is a variant of the ab initio Valence Bond (VB) theory. This code can perform RBLW calculations for close-shell systems and ROBLW calculations for open-shell systems. It can also be combined with the grid-DFT calculations. The algorithm to derive self-consistent BLW is based on:

• 1) E. Gianinetti; M. Raimondi; E. Tornaghi, Int. J. Quant. Chem. 60, 157-166(1996).
• 2) A. Famulari, E. Gianinetti, M. Raimondi, M. Sironi, I. Vandoni, Theor. Chem. Acc. 99, 358-365(1998).
• 3) Y. Mo, S. D. Peyerimhoff, J. Chem. Phys. 109, 1687-1697 (1998).
• 4) Y. Mo, J. Gao, S. D. Peyerimhoff, J. Chem. Phys. 112, 5530-5538 (2000).
• 5) L. Song, Y. Lin, Y. Mo, J. Phys. Chem. A, 111, 8291-8301 (2007).

NBLOCK = number of blocks, the definition of each block shall be listed in $BLWDAT group. If nblock=1, it’s just a regular RHF/ROHF calculation.

ITER = maximum number of BLW cycles (default=50)

SCFCOV = NONE, do not take any actions during the SCF iterations DAMP, use damping of the Fock matrix if energy rises DIIS , selects Pulay's DIIS interpolation (based on FOCK matrix) DDIIS, selects Pulay's DIIS interpolation (based on density matrix) (default=DIIS)

IFZB(1) = an array that lists the blocks to be frozen (orbitals kept unchanged) during the optimization. This is useful to examine individual polarization effects, for example.

To switch DFT calculation to full accuracy since the very first step (for the guess orbitals), de-activate coarse grid . GAMESS starts DFT with coarse grid to accelerate the calculation. But if one needs to obtain the polarized energy, the energy of the first iteration shall be exact. To do so, add the following $DFT group. to the .inp file.

 $DFT NRAD0=96 NLEB0=302 NTHE0=12 NPHI0=24 $END

$BLWDAT group (required by $BLW)

For each block:

NE NBF IFLAG

List of basis functions

where

NE is the number of electrons of that block.

NBF is the number of basis functions of that block. IFLAG is an input control.

IFLAG =

0, all the basis functions shall be specified;

1, the basis functions are sequential, and only the first one and the last one need be specified;

-1, this block has all the rest basis functions, thus no further specification.

The initial guess can be setup after the definitions of all blocks. It can be useful if the program fails to obtain convergence or one needs to derive the polarized energy term for the BLW-ED (energy decomposition) analysis. Note that the coefficients of MOs correspond to the list of basis functions in the definition lines of blocks. An blank line separates each blocks.

For example:
--------------------------------
$BLW  NBLOCK=2 $END
$BLWDAT
4 4 0       ← block 1 has 4 electrons and 4 basis functions
1 2 3 4    ← bfs of block 1
4 6 1    ← block 2 has 4 electrons and 6 basis functions
5 10     ← bfs of block 2 is from 5 to 10
1.0 0.0 0.0 0.0
0.0 1.0 0.0 0.0                ← initial guess for the 2 occupied orbitals(4/2) of block 1 
                             ← a blanck line at the end of the block (with no space)
1.0 0.0 0.0 0.0 0.0 0.0   
0.0 1.0 0.0 0.0 0.0 0.0    ← initial guess for the 2 occupied orbitals(4/2) of block 2
$END
---------------------------------

Note: Eigenvalues and compositions of BLW-MOs are stored in $SCR/*.blw.

$BLWCI group (requires $BCIDAT group)

This part of code will not be used in the present workshop. Please discuss directly with Yirong Mo if you are interested in it.

BLWCI is intended to compute the coupling between two BLW’s which usually refer to the before- and after- charge transferred states in integral-direct way. References are:

• 1) Y. Mo, W. Wu, Q. Zhang, J. Chem. Phys. 119, 6448-6456 (2003).
• 2) Mo, Y., Song, L., Liu, M., Lin, Y., Cao, Z., Wu, W., J. Chem. Theory Comput., 8, 800-805 (2012).

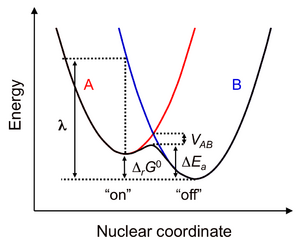
The figure illustrates the electronic coupling strength <math>V_{AB}</math> between two electron-localized states A and B as <math>V_{AB}=H_{AA}-E_{1}=\frac{H_{AA}S_{AB}-H_{AB}}{1+S_{AB}}</math>

NDET = the number of determinants

NAEQB =

0, alpha and beta orbitals are not the same, so beta orbitals shall be inputted after alpha orbital

1, alpha and beta orbitals are the same, so only alpha orbitals will be inputted (default)

$BCIDAT group (required by $BLWCI)

The coefficients of occupied MOs for each configuration shall be given here.

occupied orbitals of 1st determinant

occupied orbitals of 2nd determinant