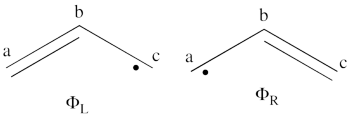VBTutorial2

<< Return to the program

VB applications on PI systems

In all the following exercises, <math>\pi</math> the system will be taken as active, and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule.

Main exercises

Exercise 1 : The allyl radical Paper exercise Covalent structures of the allyl radical : What are the three possible covalent structures for the allyl radical molecule ? Use the thumb rules of qualitative VB theory to compute their energy, and show that two of them are degenerate. Show that the third structure can be expressed as a linear combination of the first two structures, and thus that only two of the three covalent structures form a complete basis of non-redundant structures (Rumer basis). Understanding the pattern of spin density distributions in the allyl radical as found in EPR spectroscpy. Express the wave functions of the non-redundant structures (from 1.1) of allyl radical in terms of the VB determinant. Write the wave function of the ground state of the allyl radical as a negative combination of the wave functions of the non-redundant structures. Based on the expression of the spin density <math> \rho_s </math> <math> {\rho_k}^s = N^2 \sum_i {c_i}^2 {\delta_{ki}}</math> propose the spin density distribution in the allyl radical. In the above equation N is a normalization constant, c is the coefficient of the VB determinant in the wave function and <math> \delta </math> is either +1 or -1 depending on whether the electron which is located on atom k in the ith determinant is <math> \alpha </math> or <math> \beta </math> spin, respectively. Show pictorially: Why your spin density is polarized. What would be the spin density pattern in pentadienyl radical? What would be the spin density in the excited state of allyl radical (taking into account that resulting wave function is a positive combination of the <math> \Phi_L </math> and <math> \Phi_R </math> wave functions? Covalent and ionic structures of the allyl radical : What are the possible ionic structures for the allyl radical ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures. Answer 1. 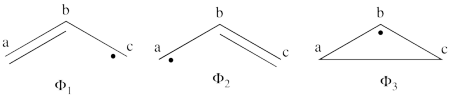Covalent structures of the allyl radical: The following are the three possible covalent structures: According to the thumb rules of qualitative VB theory (given in lecture I), both <math> \Phi_1 </math> and <math> \Phi_2 </math> display an unpaired electron in the vicinity of one end of a covalent bond. The energy for this repulsion is <math> -\beta</math>S, while the energy of the covalent bond is <math> 2\beta</math>S. Therefore, the total energy for either <math> \Phi_1 </math> or <math> \Phi_2 </math> is <math> \beta</math>S. For <math> \Phi_3 </math>, the unpaired electron is in the vicinity of both ends of the covalent bond, therefore the corresponding repulsion is twice <math> -\beta</math>S. As for the energy of the covalent bond, it can be neglected since it is a "long" bond, between atoms that are not neighbors. So the total energy for <math> \Phi_3 </math> is <math> -2\beta</math>S. <math> \Phi_{\textrm{1}} = \vert a\bar{b}c\vert - \vert \bar{a}bc\vert </math> <math> \Phi_2 = \vert ab\bar{c}\vert - \vert a\bar{b}c\vert </math> <math> \Phi_3 = \vert ab\bar{c}\vert - \vert \bar{a}bc\vert = \Phi_1 + \Phi_2 </math> Since <math> \Phi_{\textrm{3}} </math> is the positive combination of <math> \Phi_{\textrm{1}} </math> and <math> \Phi_{\textrm{2}} </math> the two first structures form a complete basis of non-redundant structures. 2.Understanding the pattern of spin density distributions in the allyl radical as found in EPR spectroscopy The wave functions of the non-redundant structures are <math> \Phi_L = \frac{1}{\sqrt2}[\vert a\bar{b}c\vert - \vert \bar{a}bc\vert] </math> <math> \Phi_R = \frac{1}{\sqrt2}[\vert ab\bar{c}\vert - \vert a\bar{b}c\vert] </math> The negative combination of these two wave functions determines the ground state wave-function of allyl radical <math> \Phi_{GS}= \Phi_L - \Phi_R= \frac{1}{\sqrt6}[2\vert a\bar{b}c\vert - \vert \bar{a}bc\vert - \vert ab\bar{c}\vert] </math> We note with that respect that the determinant with the largest coefficient in the ground state is the spin-alternant determinant. We can see that the weight of this spin-alternant determinant is four times larger than the corresponding weights of the two other determinants. This, as we will show later can explain the polarization of the spin density. Now, let's use the following expression for the spin density: <math> \rho_k= N^2 \sum_i {c_i}^2 {\delta_{ki}} </math> to calculate the spin density distribution in the allyl radical: <math> \rho_a = \frac{1}{6}[4 - 1 + 1] = \frac{2}{3} </math> <math> \rho_b = \frac{1}{6}[-4 + 1 + 1] = -\frac{1}{3} </math> <math> \rho_c = \frac{1}{6}[4 + 1 - 1] = \frac{2}{3} </math> Since <math> \Phi_{GS} </math> is dominated by the spin-alternant determinant <math> \vert a\bar{b}c\vert </math>, (as mentioned before, it has the largest coefficient in the ground state), the spin distribution properties could in fact be predicted without any calculation, but just by looking at the spin-alternant determinant. 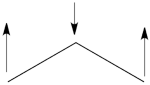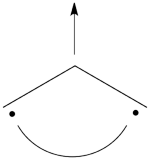Here is a pictorial representation of the spin-alternant determinant. It is clear that it predicts spin polarization with a spin-down on the central carbon atom and spin-up on the two terminals. As such, (since it dominates the ground state wave-function) it is predicted that the ground state wave function will exhibit the same spin distribution. In other words, in principle, in this case it could be sufficient to look at this spin-alternant determinant to get a qualitative correct estimate of the spin distribution. 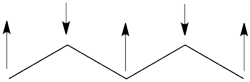The spin-alternant determinant will generally dominate the wave function of the ground state for the entire series of conjugated radicals. For example, if we wish to predict/understand the spin density patterns of the pentadienyl radical, all we have to do is draw the spin-alternant determinant. Thus, as shown below for pentadienyl the central carbon atom has spin up, and the spins alternate in direction on both sides. The next radical in line (with 7 carbons) will have a similar spin distribution as in allyl, with spin-down in the center flanked by spin-ups on both sides, etc. Lets turn now to the excited state of allyl radical. Since the ground state is the negative combination of the <math> \Phi_L </math> and <math> \Phi_R </math> structures above, the excited state is the corresponding positive combination. This positive combination eliminates the spin-alternant determinant, and we remain with: <math> \Phi_{EXS} = \Phi_L + \Phi_R= \frac{1}{\sqrt2}[\vert ab\bar{c}\vert -\vert \bar{a}bc\vert ] </math> Pictorially, this is simply the cyclopropyl structure with spin density localized only on the central carbon: Note how the spin switches from the ground- to the excited state. It is generally true that in the first excited state of the polyenyl radicals, the spin alternant determinant vanishes and the spin density is determined by the long bond structures. 3. 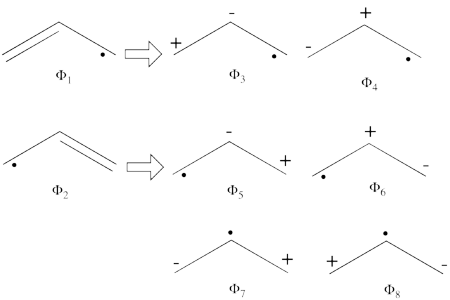Covalent and ionic structures of the allyl radical: From each covalent structure we can get two ionic structures. Additional two ionic structures are obtained from the redundant structure. Therefore overall there are 6 different ionic structures In the two ionic structures (<math> \Phi_{\textrm{7}} </math>,<math> \Phi_{\textrm{8}} </math>) that are based on the redundant structure the charges are farther from each otehr compared with the other ionic structures and are thereofre, expected to be higher in energy. These two structures will therefore not be included in our chosen sub-set of structures. Computer Exercise Computation of covalent state of allyl radical Compute the VBSCF wave function for the covalent state of the allyl radical (6-31G* basis set) using the covalent structures you have chosen (paper Ex. 1.2). What are the weights of the different VB structures. Was that expected? What is the wavefunction in determinant description? What is the spin population? Do the calculated results agree with your answer for paper Ex. 2.1? Repeat the calculation for the first excited state using "nstate=1" . What is the the wavefunction? Use determinant description. What is the spin population in this case? Was that expected? Computation of allyl radical energy and weights: Compute a VBSCF wave function for allyl radical (6-31G* basis set) using your selected set of structures (questions 1.2 and 3.1). Compute a VBSCF wave function including the complete set of VB structures (the adiabatic wavefunction), using the "str=full" keyword. Compare the weights and energies for both wave functions to validate your selection of structures. Compute for allyl radical a BOVB wave function which includes only your selected set of most chemically meaningful structures (remember to use the guess orbitals obtained at the VBSCF level). Compare the weights obtained at the VBSCF and BOVB levels. Computation of resonance energies : We want to build a wave-function corresponding to only one Lewis (diabatic) structure for the allyl radical. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated with this covalent bond. Propose a selection of VB structures which would describe one Lewis structure for the allyl radical. Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl radical at the BOVB level. The resonance energy is calculated as the difference between the adiabatic state and the Lewis (diabatic) state of the allyl radical. >> Answer Exercise 2 : Radical character of ozone Computer Exercises Propose a complete basis of non-redundant VB structures for the ozone molecule. Based on your chemical knowledge, propose a selection subset of the most chemically meaningful structures. (Paper exercise) Compute a VBSCF wave function for ozone (6-31G basis set) using your selected set of structures. Compute a VBSCF wave function including the complete set of VB structures, using the "str=full" keyword. Compare the weights and energies for both wave functions to validate your selection of structures. Compute a BOVB wave function for ozone which includes only your selected set of most chemically meaningful structures (use the guess orbitals obtained at the VBSCF level). Compare the weights obtained at the VBSCF and BOVB level. Compare the BOVB diradical weight to the value predicted by simple MO theory. For your convenience the MO wave function is as follows <math> \psi_{H\ddot{u}ckel} = 25%\Phi_1 + 25%\Phi_2 + 12.5%\Phi_3 + 25%\Phi_4 + 6.25%\Phi_5 + 6.25%\Phi_6 </math> (consult the following paper exercise) Paper Exercises - Optional/Homework Use the HuLis software to retrieve the Hückel MOs for ozone. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures (consult the hint given below). Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). What is the radical character of ozone according to simple MO theory? Hint - It is useful to use here the electron hole equivalence for details consult: >> The electron-hole equivalence >> Answer

Optional Exercises - Homework

Exercise 3 : Resonance energy of Benzene ***** EXERCISE AND INPUT FILES TO BE WRITTEN ***** Computer Exercise Covalent state of benzene : Propose a complete basis of non-redondant covalent VB structures for benzene. (hint there should be 5 structures). Compute benzene with str=cov (6-31G basis set), and analyze the structures obtained. Were you right in your description of the covalent structures? now repeat the calculation with only 1 of the kékulé strucures and estimate the Vertical Resonance Energy (VRE) Full description of benzene : Compute a VBSCF wave function including the complete set of VB structures, using the "str=full" keyword. How many structures are available overall? In principle in order to calcuate properly the VRE one has to compute the energy difference between the overall adiabatic state of benzene and a corresponding Kékulé diabatic state. The latter Kékulé state requires an overall of 27 structures for its proper description, which have to be hand-written(!) One solution is the use of semi-localized orbitals offered by the "Bond Distorted Orbitals" option. Calculate the energy of one Kékulé state using the BDO (see BDO procedue below). Compare the energy of the covalent Kékulé structure calculated with HAO (hybrid atomic orbitals) and BDO. What is the reason for the difference? Estimate the corresponding VRE, has it improved? BDO procedue First run standard VBSCF calculation with the following keywords (frgtyp=sao, orbtype=hao and guess=auto). Copy the file file_name.orb which was created in the previous step, to a new file new_file_name.gus. Copy the file file_name.xmi to new_file_name.xmi and modify it as follows: Use guess=read and orbtyp=bdo. frgtyp keyword is not required for this type of calculation (no need of $frag part in the input). Modify $orb part according to new_file_name.gus This BDO procedure enables inclusion of all ionic structures associated with the given Kékulé structure implicitly. >> Answer Exercise 4 : The allyl cation Paper Exercise Structures of the allyl cation, and weights from Hückel theory : Find a complete basis of covalent structures for the allyl cation. What are the possible ionic structures for the allyl cation ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures. Use the HuLis software to retrieve the Hückel MOs for allyl cation. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures. Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). Computer Exercise Computation of allyl cation energies and weights : Compute a VBSCF wave function for allyl cation (6-31G basis set) using your selected set of structures (questions 1.3 and 2.2). Compute a VBSCF wave function including the complete set of VB structures, using the "str=full" keyword. Compare the weights and energies for both wave functions to validate your selection of structures. Compute for allyl cation a BOVB wave function which include only your selected set of most chemically meaningful structures (use the guess orbitals obtained at the VBSCF level). Compare the weights obtained at the VBSCF and BOVB level. Compare the BOVB weights to the weights predicted by simple MO theory. Computation of resonance energies : We want to build a wave-function corresponding to only one Lewis structures for the allyl cation. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated to this covalent bond. Propose a selection of VB structures which would describe one Lewis structure for the allyl cation. Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl cation at the BOVB level. >> Answer

>> general guidelines for BOVB calculations