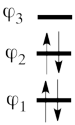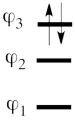The electron-hole equivalence
The electron-hole equivalence
In the present case, this equivalence can be used to transform a problem of 4-orbital determinants into a simpler problem of 2-orbital determinants.
This goes as follows. Whether we reason in the MO framework or in the VB framework, the basis set of orbitals is made of 3 spin-up spinorbitals and 3 spin-down ones. So for each 4-e determinant involving 4 occupied spin-orbitals, we can define a 2-hole determinant involving 2 spin-orbitals, filled with « holes ». Holes have spins and can be represented by up or down arrows just like electrons. There is a one-to-one correspondence between the electron-determinants and the hole-determinants, as shown below :
| electron-filled determinants | hole-filled determinants | |
|---|---|---|
 |
| |
| <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> | <=> | <math>\vert \varphi_3\bar{\varphi_3}\vert </math> |
| Expand into | Expand into | |
| <math> \Phi_{\textrm{1}}= \frac{1}{\sqrt2}(\vert p_1\overline p_1p_2\overline p_3\vert + \vert p_1\overline p_1p_3\overline p_2\vert </math> | <=> | <math> \frac{1}{\sqrt2}(\vert p_2\overline p_3 \vert + \vert p_3\overline p_2\vert </math> |
| <math> \Phi_{\textrm{2}}= \frac{1}{\sqrt2}(\vert p_3\overline p_3p_1\overline p_2\vert + \vert p_3\overline p_3p_2\overline p_1\vert </math> | <=> | <math> \frac{1}{\sqrt2}(\vert p_1\overline p_2 \vert + \vert p_2\overline p_1\vert </math> |
| <math> \Phi_{\textrm{3}}= \frac{1}{\sqrt2}(\vert p_2\overline p_2p_1\overline p_3\vert + \vert p_2\overline p_2p_3\overline p_1\vert </math> | <=> | <math> \frac{1}{\sqrt2}(\vert p_1\overline p_3 \vert + \vert p_3\overline p_1\vert </math> |
| <math> \Phi_{\textrm{4}}= \vert p_1\overline p_1p_3\overline p_3\vert </math> | <=> | <math> \vert p_2\overline p_2 \vert </math> |
| <math> \Phi_{\textrm{5}}= \vert p_1\overline p_1p_2\overline p_2\vert </math> | <=> | <math> \vert p_3\overline p_3 \vert </math> |
| <math> \Phi_{\textrm{6}}= \vert p_2\overline p_2p_3\overline p_3\vert </math> | <=> | <math> \vert p_1\overline p_1 \vert </math> |
So instead of expanding the Hartree-Fock electron determinant <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> into VB structures, which is complicated, we better expand the smaller complementary hole-determinant <math>\vert \varphi_3\bar{\varphi_3}\vert </math> into VB structures where each contains two holes. Once this is done, it suffices to use the table above to go back to the 4-electron VB structures (e.g. <math> \vert p_2\overline p_2 \vert </math> => <math> \vert p_1\overline p_1p_3\overline p_3\vert </math> and so on). This latter transformation gives us the final 4-e VB function.