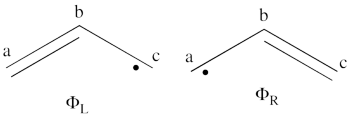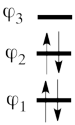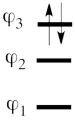Différences entre les versions de « VBTutorial2 »
| (31 versions intermédiaires par 3 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | [[ | + | [[VB_tutorial|<<< VB tutorials main page]] |
| − | |||
| Ligne 6 : | Ligne 5 : | ||
In all the following exercises, '''<font color=red><math>\pi</math> the system will be taken as active</font>''', and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule. | In all the following exercises, '''<font color=red><math>\pi</math> the system will be taken as active</font>''', and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule. | ||
| − | + | The excersise involves calculation of all the electrons. Yet, in principle the <math>\sigma</math> system could aslo be frozen by using the bfi option. Thus, such inputs/outputs are also given however, to avoid redundency, the results from these inputs are not summarized. | |
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
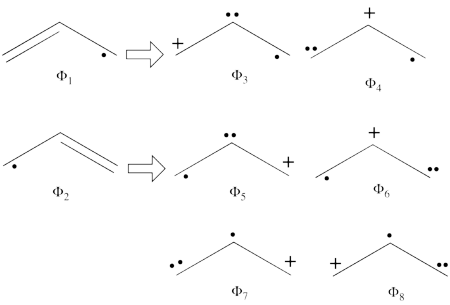
| Ligne 53 : | Ligne 52 : | ||
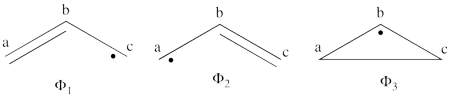
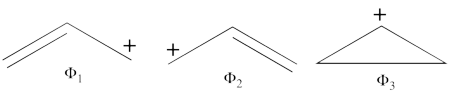
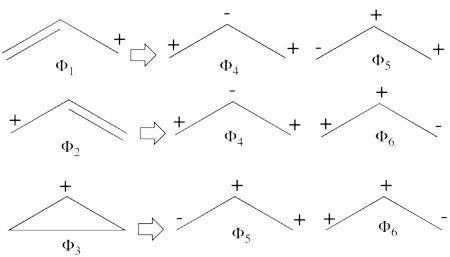
<br>Since <math> \Phi_{\textrm{3}} </math> is the positive combination of <math> \Phi_{\textrm{1}} </math> and <math> \Phi_{\textrm{2}} </math> the two first structures form a complete basis of non-redundant structures. | <br>Since <math> \Phi_{\textrm{3}} </math> is the positive combination of <math> \Phi_{\textrm{1}} </math> and <math> \Phi_{\textrm{2}} </math> the two first structures form a complete basis of non-redundant structures. | ||
<br> | <br> | ||
| + | |||
====2.''Understanding the pattern of spin density distributions in the allyl radical as found in EPR spectroscopy''==== | ====2.''Understanding the pattern of spin density distributions in the allyl radical as found in EPR spectroscopy''==== | ||
| Ligne 89 : | Ligne 89 : | ||
====3. ''Covalent and ionic structures of the allyl radical:'' ==== | ====3. ''Covalent and ionic structures of the allyl radical:'' ==== | ||
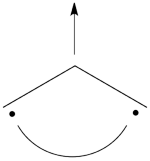
| − | #From each covalent structure we can get two ionic structures. Additional two ionic structures are obtained from the redundant structure. Therefore overall there are 6 different ionic structures <br>[[File:Allyl_Ionic- | + | #From each covalent structure we can get two ionic structures. Additional two ionic structures are obtained from the redundant structure. Therefore overall there are 6 different ionic structures <br>[[File:Allyl_Ionic-N2.png|450px]] <br> In the two ionic structures (<math> \Phi_{\textrm{7}} </math>,<math> \Phi_{\textrm{8}} </math>) that are based on the redundant structure the charges are farther from each other compared with the other ionic structures and are therefore, expected to be higher in energy. These two structures will therefore not be included in our chosen sub-set of structures. |
|} | |} | ||
| Ligne 116 : | Ligne 116 : | ||
|- | |- | ||
| | | | ||
| + | |||
====''1. Computation of covalent state of allyl radical''==== | ====''1. Computation of covalent state of allyl radical''==== | ||
# The weights of the two structures, <math> \Phi_1 </math> and <math> \Phi_{\textrm{2}} </math> is identical and equals 0.5 as expected. | # The weights of the two structures, <math> \Phi_1 </math> and <math> \Phi_{\textrm{2}} </math> is identical and equals 0.5 as expected. | ||
| Ligne 193 : | Ligne 194 : | ||
==== ''3. Computation of resonance energies for the Allyl radical'' ==== | ==== ''3. Computation of resonance energies for the Allyl radical'' ==== | ||
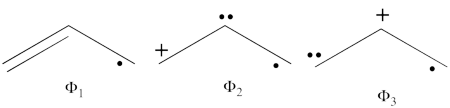
| − | #The following are the three structures of allyl radical which describe one of its Lewis structures (the structure which involves a bond between atoms a and b and an unpaired electron on atom c):<br>[[File: | + | #The following are the three structures of allyl radical which describe one of its Lewis structures (the structure which involves a bond between atoms a and b and an unpaired electron on atom c):<br>[[File:Allyl_Lewis1.png|450px]] <br> <br> |
#The total energy of the VB wave function of this Lewis structure is summarized in the following table: <br> <br> | #The total energy of the VB wave function of this Lewis structure is summarized in the following table: <br> <br> | ||
{| border="1" | {| border="1" | ||
| Ligne 214 : | Ligne 215 : | ||
|} <br> At the BOVB level, the resonance energy (RE) of the allyl radical which is the difference between the total energy of the allyl radical with full set of the structures and the total energy of the Lewis structure only is RE = 22.5 kcal/mol. | |} <br> At the BOVB level, the resonance energy (RE) of the allyl radical which is the difference between the total energy of the allyl radical with full set of the structures and the total energy of the Lewis structure only is RE = 22.5 kcal/mol. | ||
|} | |} | ||
| + | |||
| + | [[VBFile 2-1 | FILES FOR Exersice1]] | ||
|} | |} | ||
| Ligne 242 : | Ligne 245 : | ||
|- | |- | ||
| | | | ||
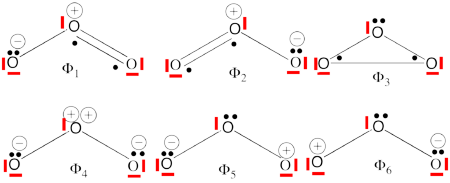
| − | #Complete set of the non-redundant VB structures of the ozone are <br/>[[File:Ozone- | + | #Complete set of the non-redundant VB structures of the ozone are (the red line represents the <math> \sigma - electrons </math>) <br/>[[File:Ozone-full2.png|450px]]<br> <math> \Phi_{\textrm{1}}= \frac{1}{\sqrt2}(\vert p_1\overline p_1p_2\overline p_3\vert + \vert p_1\overline p_1p_3\overline p_2\vert) |
</math><br> <math> | </math><br> <math> | ||
\Phi_{\textrm{2}}= \frac{1}{\sqrt2}(\vert p_3\overline p_3p_1\overline p_2\vert + \vert p_3\overline p_3p_2\overline p_1\vert) | \Phi_{\textrm{2}}= \frac{1}{\sqrt2}(\vert p_3\overline p_3p_1\overline p_2\vert + \vert p_3\overline p_3p_2\overline p_1\vert) | ||
| Ligne 310 : | Ligne 313 : | ||
|} | |} | ||
| − | + | [[VBFile 2-2 | FILES FOR Exercise2]] | |
|} | |} | ||
| Ligne 320 : | Ligne 323 : | ||
# Use the [http://www.hulis.free.fr/ HuLis] software to retrieve the Hückel MOs for ozone. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures (consult the hint given below). | # Use the [http://www.hulis.free.fr/ HuLis] software to retrieve the Hückel MOs for ozone. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures (consult the hint given below). | ||
# Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). What is the radical character of ozone according to simple MO theory? <br> | # Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). What is the radical character of ozone according to simple MO theory? <br> | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Answer''' | ||
| + | |- | ||
| + | | | ||
| + | # The MO orbitals in the Huckel approximation for ozone are: <br> <math> | ||
| + | \varphi_1 = \frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3) </math> <br> <math> | ||
| + | \varphi_2 = \frac{1}{\sqrt2}(p_1 - p_3)</math> <br> <math> | ||
| + | \varphi_3 = \frac{1}{2}(p_1 - \sqrt{2}p_2 + p_3) | ||
| + | |||
| + | </math> <br> <br> A single-determinant MO wavefunction of ozone based on these Hückel orbitals would look as follows: <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert = | ||
| + | \vert [\frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)][\overline{\frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)]}[\frac{1}{\sqrt2}(p_1 - p_3)][\overline{\frac{1}{\sqrt2}(p_1 - p_3)]} \vert | ||
| + | |||
| + | </math> <br> However, we can simplify the problem by using the electron/hole equivalence: [[The electron-hole equivalence|>> ''the electron-hole equivalence'']]<br> <br> Thus, we simply replace holes by electrons and vise versa in <math> \psi_{H\ddot{u}ckel} </math> getting a function of <math> {\psi_{H\ddot{u}ckel}}^{hole} </math>, which we will then expande in terms of VB structures. Finally, we will perform the back hole-electron transformation in the VB representation to get the final result. This way we transform a 4e-3c problem into 2h-3c one.<br> <br> <math> | ||
| + | |||
| + | {\psi_{H\ddot{u}ckel}}^{hole} = \vert \varphi_3\bar{\varphi_3}\vert = \frac{1}{4} \vert (p_1 - \sqrt{2}p_2 + p_3)\overline{(p_1 - \sqrt{2}p_2 + p_3)} \vert | ||
| + | |||
| + | </math><br> <br> Expanding into AO determinants, we get:<br> <br> <math> | ||
| + | |||
| + | {\psi_{H\ddot{u}ckel}}^{hole} = \frac{1}{4} (\vert (p_1\overline p_3 \vert + \vert (p_3\overline p_1 \vert) - \frac{\sqrt{2}}{4}(\vert p_1\overline p_2 \vert + \vert p_2 \overline p_1 \vert) - \frac{\sqrt{2}}{4}(\vert p_2\overline p_3 \vert + \vert p_3 \overline p_2 \vert) + \frac{1}{4} \vert p_1\overline p_1 \vert + \frac{1}{4} \vert p_3\overline p_3 \vert + \frac{1}{2} \vert p_2\overline p_2 \vert | ||
| + | |||
| + | </math><br> <br> Doing the electron-hole back transformation, we get: <br> <br> <math> | ||
| + | |||
| + | \psi_{H\ddot{u}ckel} = \frac{\sqrt{2}}{4}\Phi_3 - \frac{1}{2}\Phi_1 - \frac{1}{2}\Phi_2 + \frac{1}{4}\Phi_6 + \frac{1}{4}\Phi_5 + \frac{1}{4}\Phi_4 | ||
| + | |||
| + | </math><br> <br> | ||
| + | #The corresponding weights while neglecting overlap (for simplicity) are therefore:<br> <br><math> | ||
| + | |||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | 25%\Phi_1 + | ||
| + | 25%\Phi_2 + 12.5%\Phi_3 + | ||
| + | 25%\Phi_4 + 6.25%\Phi_5 + | ||
| + | 6.25%\Phi_6 | ||
| + | |||
| + | </math><br> <br>Thus, according to simple MO theory the radical character of ozone is 12.5%. | ||
| + | |} | ||
| + | |||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| Ligne 332 : | Ligne 374 : | ||
|- | |- | ||
| | | | ||
| + | <small> | ||
In the present case, this equivalence can be used to transform a problem of 4-orbital determinants into a simpler problem of 2-orbital determinants. | In the present case, this equivalence can be used to transform a problem of 4-orbital determinants into a simpler problem of 2-orbital determinants. | ||
This goes as follows. Whether we reason in the MO framework or in the VB framework, the basis set of orbitals is made of 3 spin-up spinorbitals and 3 spin-down ones. So for each 4-e determinant involving 4 occupied spin-orbitals, we can define a 2-hole determinant involving 2 spin-orbitals, filled with « holes ». Holes have spins and can be represented by up or down arrows just like electrons. There is a one-to-one correspondence between the electron-determinants and the hole-determinants, as shown below : | This goes as follows. Whether we reason in the MO framework or in the VB framework, the basis set of orbitals is made of 3 spin-up spinorbitals and 3 spin-down ones. So for each 4-e determinant involving 4 occupied spin-orbitals, we can define a 2-hole determinant involving 2 spin-orbitals, filled with « holes ». Holes have spins and can be represented by up or down arrows just like electrons. There is a one-to-one correspondence between the electron-determinants and the hole-determinants, as shown below : | ||
| Ligne 371 : | Ligne 414 : | ||
<br> | <br> | ||
So instead of expanding the Hartree-Fock electron determinant <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> into VB structures, which is complicated, we better expand the smaller complementary hole-determinant <math>\vert \varphi_3\bar{\varphi_3}\vert </math> into VB structures where each contains two holes. Once this is done, it suffices to use the table above to go back to the 4-electron VB structures (e.g. <math> \vert p_2\overline p_2 \vert </math> => <math> \vert p_1\overline p_1p_3\overline p_3\vert </math> and so on). This latter transformation gives us the final 4-e VB function. | So instead of expanding the Hartree-Fock electron determinant <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> into VB structures, which is complicated, we better expand the smaller complementary hole-determinant <math>\vert \varphi_3\bar{\varphi_3}\vert </math> into VB structures where each contains two holes. Once this is done, it suffices to use the table above to go back to the 4-electron VB structures (e.g. <math> \vert p_2\overline p_2 \vert </math> => <math> \vert p_1\overline p_1p_3\overline p_3\vert </math> and so on). This latter transformation gives us the final 4-e VB function. | ||
| − | + | </small> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| Ligne 414 : | Ligne 420 : | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| Ligne 423 : | Ligne 426 : | ||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| − | !<big><big>'''Optional Exercises - Homework'''</big> | + | !<big><big>'''Optional Exercises - Homework'''</big></big> |
|- | |- | ||
| | | | ||
== Exercise 3 : Resonance energy of Benzene == | == Exercise 3 : Resonance energy of Benzene == | ||
| − | |||
| − | |||
| − | |||
# Covalent state of benzene : | # Covalent state of benzene : | ||
## Propose a complete basis of non-redondant covalent VB structures for benzene. (hint there should be 5 structures). | ## Propose a complete basis of non-redondant covalent VB structures for benzene. (hint there should be 5 structures). | ||
| Ligne 437 : | Ligne 437 : | ||
# Full description of benzene : | # Full description of benzene : | ||
## Compute a VBSCF wave function including the complete set of VB structures, using the "str=full" keyword. How many structures are available overall? | ## Compute a VBSCF wave function including the complete set of VB structures, using the "str=full" keyword. How many structures are available overall? | ||
| − | ## In principle in order to calcuate properly the VRE one has to compute the energy difference between the overall adiabatic state of benzene and a corresponding Kékulé diabatic state. The latter Kékulé state requires an overall of 27 structures for its proper description, which have to be hand-written(!) One solution is the use of semi-localized orbitals offered by the "Bond Distorted Orbitals" option. Calculate the energy of one Kékulé state using the BDO (see BDO | + | ## In principle in order to calcuate properly the VRE one has to compute the energy difference between the overall adiabatic state of benzene and a corresponding Kékulé diabatic state. The latter Kékulé state requires an overall of 27 structures for its proper description, which have to be hand-written(!) One solution is the use of semi-localized orbitals offered by the "Bond Distorted Orbitals" option. Calculate the energy of one Kékulé state using the BDO (see BDO procedure below). Compare the energy of the covalent Kékulé structure calculated with HAO (hybrid atomic orbitals) and BDO. What is the reason for the difference? |
## Estimate the corresponding VRE, has it improved? | ## Estimate the corresponding VRE, has it improved? | ||
{| class="collapsible collapsed wikitable" | {| class="collapsible collapsed wikitable" | ||
|- | |- | ||
| − | !''BDO | + | !<small>''BDO procedure''</small> |
|- | |- | ||
| | | | ||
| + | <small> | ||
# First run standard VBSCF calculation with the following keywords (frgtyp=sao, orbtype=hao and guess=auto). | # First run standard VBSCF calculation with the following keywords (frgtyp=sao, orbtype=hao and guess=auto). | ||
# Copy the file '''file_name.orb''' which was created in the previous step, to a new file '''new_file_name.gus'''. | # Copy the file '''file_name.orb''' which was created in the previous step, to a new file '''new_file_name.gus'''. | ||
| Ligne 451 : | Ligne 452 : | ||
## ''frgtyp'' keyword is not required for this type of calculation (no need of $frag part in the input). | ## ''frgtyp'' keyword is not required for this type of calculation (no need of $frag part in the input). | ||
## Modify $orb part according to '''new_file_name.gus''' | ## Modify $orb part according to '''new_file_name.gus''' | ||
| − | |||
This BDO procedure enables inclusion of all ionic structures associated with the given Kékulé structure implicitly. | This BDO procedure enables inclusion of all ionic structures associated with the given Kékulé structure implicitly. | ||
| + | </small> | ||
|} | |} | ||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Answer''' | ||
| + | |- | ||
| + | | | ||
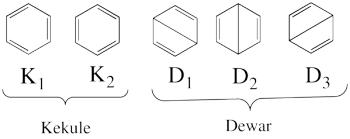
| + | ====''Covalent state of benzene''==== | ||
| + | * The following are the five covalent structures of the benzene: <br/>[[File:Benzene_5CovStruct.png|350px]]<br> | ||
| + | These structures consist of 2 Kekule (<math> K_1 </math> and <math> K_2 </math>) and 3 Dewar (<math> D_1, </math> <math> D_2 </math> and <math> D_3 </math>) structures. | ||
| + | <br> | ||
| + | <br> | ||
| + | * VB energies of benzene's covalent state are summarized in the following Table: | ||
| + | {| border="1" | ||
| + | |+ | ||
| + | ! scope="col" | Structures & Method | ||
| + | ! scope="col" | Total Energy (au) | ||
| + | |- | ||
| + | ! scope="row" | 5 covalent (VBSCF) | ||
| + | | -230.54451931 | ||
| + | |- | ||
| + | ! scope="row" | 1 covalent (VBSCF) | ||
| + | | -230.49584123 | ||
| + | |- | ||
| + | ! scope="row" | 5 covalent(BOVB) | ||
| + | | -230.545495 | ||
| + | |} | ||
| + | |||
| + | The vertical resonance energy can be obtained by the difference between the energy of the state which includes all 5 covalent structures and only 1 Kekule structure. Thus, this VRE is calculated to be '''VRE''' = 30.55 kcal/mol (VBSCF) and 31.16 kcal/mol (BOVB). These values are too low when compared to the experimental value which is 65 kcal/mol (estimated by use of thermochemistry and empirical force constant. Chemical Review, '''101''', 1501-1539 (2001)) | ||
| + | <br> | ||
| + | |||
| + | ====''Full description of benzene''==== | ||
| + | # The complete number of the ionic structures is too large to be written by hand. So using the keyword "str=full" produces all covalent and ionic structures. For benzene this involves overall of 175 structures. | ||
| + | # In order to calculate the Kékulé diabatic state one has to calculate the Kékulé covalent structure along with all the related ionic structures (overall of 27 structures in this case). The keyword "str=full" cannot be used in this case, thus, in order to avoid tedious work we utilize the bond distorted orbitals '''bdo''' while calculating only the covalent structure. <br> The following Table summarizes the energies for the diabatic Kékulé state as well as the adiabatic state of benzene: | ||
| + | |||
| + | {| border="1" | ||
| + | |+ diabatic and adiabatic energies of benzene | ||
| + | ! scope="col" | Structures & Method | ||
| + | ! scope="col" | Total Energy (au) | ||
| + | |- | ||
| + | ! scope="row" | 1 Kekule ('''orbtyp=hao''') (VBSCF) | ||
| + | | -230.49584123 | ||
| + | |- | ||
| + | ! scope="row" | 1 Kekule ('''orbtyp=bdo''') (VBSCF) | ||
| + | | -230.58675751 | ||
| + | |- | ||
| + | ! scope="row" | 175 structures ('''str=full''') (VBSCF) | ||
| + | | -230.69492368 | ||
| + | |} | ||
| + | <br> | ||
| + | * The covalent Kékulé structure calculated with HAO (hybrid atomic orbitals) is 57 kcal/mol higher in energy than that calculated with the bond distorten orbitals (BDO). The reason is that the BDO calculation imcludes implicitely all the related ionic structures, which are important for the description of the state. | ||
| + | * The resonance energy '''RE''' = 67.9 kcal/mol (VBSCF) which is in good agreement with the experimental value (65 kcal/mol) | ||
| + | |} | ||
| − | [[ | + | [[VBFile 2-3 | FILES FOR Exercise3]] |
== Exercise 4 : The allyl cation == | == Exercise 4 : The allyl cation == | ||
| − | + | ||
| − | + | {| class="collapsible collapsed wikitable" | |
| + | |- | ||
| + | !<big>'''Paper exercise'''</big> | ||
| + | |- | ||
| + | | | ||
# Structures of the allyl cation, and weights from Hückel theory : | # Structures of the allyl cation, and weights from Hückel theory : | ||
## Find a complete basis of covalent structures for the allyl cation. | ## Find a complete basis of covalent structures for the allyl cation. | ||
## What are the possible ionic structures for the allyl cation ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures. | ## What are the possible ionic structures for the allyl cation ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures. | ||
| − | ## Use the [http://www.hulis.free.fr/ HuLis] software to retrieve the Hückel MOs for allyl cation. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures. Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). <br> <br> | + | ## Use the [http://www.hulis.free.fr/ HuLis] software to retrieve the Hückel MOs for allyl cation. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures. Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). |
| − | < | + | |
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Answer''' | ||
| + | |- | ||
| + | | | ||
| + | ====''Structures of the allyl cation, and weights from Hückel theory: ''==== | ||
| + | # There are three covalent structures for the allyl cation as follows:<br> [[File:Allyl_CovCation-N1.png|450px]] <br> the third covalent structure is expeceted to be higher in energy than the other two structures and thus, contribute less. | ||
| + | #From each covalent structure we can get two ionic structures. Some of them are however common, leading to an overall of 3 different ionic structures (<math> \Phi_{\textrm{4}} </math>, <math> \Phi_{\textrm{5}} </math>, <math> \Phi_{\textrm{6}} </math>). <br> [[File:Allyl_IonCation-N1.png|450px]] <br> (<math> \Phi_{\textrm{5}} </math> and <math> \Phi_{\textrm{6}} </math>) are expected to be high in energy. Therefore, our selected subset will involve 4 strucutres, (<math> \Phi_1, \Phi_2, \Phi_3 </math> and <math> \Phi_{\textrm{4}} </math>). | ||
| + | #The MO orbitals in the Huckel approximation are: <br> <math> | ||
| + | \varphi_1 = \frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3) </math> <br> <math> | ||
| + | \varphi_2 = \frac{\sqrt2}{2}(p_1 - p_3)</math> <br> <math> | ||
| + | \varphi_3 = \frac{1}{2}(p_1 - \sqrt{2}p_2 + p_3) </math> <br> A single-determinant MO wavefunction of allyl cation based on these Hückel orbitals would look as follows: <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = \vert \varphi_1\bar{\varphi_1}\vert = | ||
| + | \vert \frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)\overline{\frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)}\vert | ||
| + | </math> <br> Developing it into the basis atomic orbitals we get: <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | \frac{1}{4}(\vert p_1 \overline p_1\vert + \sqrt{2}\vert p_1 \overline p_2\vert + \vert p_1 \overline p_3\vert + | ||
| + | \sqrt{2}\vert p_2 \overline p_1\vert + 2\vert p_2 \overline p_2\vert + \sqrt{2}\vert p_2 \overline p_3\vert + | ||
| + | \vert p_3 \overline p_1\vert + \sqrt{2}\vert p_3 \overline p_2\vert + \vert p_3 \overline p_3\vert) = | ||
| + | </math> <br> we will now reorder the components: <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | \frac{1}{2}(\vert p_2\overline p_2\vert) + | ||
| + | \frac{1}{4}(\vert p_1\overline p_1\vert) + \frac{1}{4}(\vert p_3\overline p_3\vert) + | ||
| + | \frac{\sqrt2}{4}(\vert p_1\overline p_2\vert) - (\vert \overline p_1 p_2\vert) + | ||
| + | \frac{\sqrt2}{4}(\vert p_2\overline p_3\vert) - (\vert \overline p_3 p_2\vert) + | ||
| + | \frac{1}{4}(\vert p_1\overline p_3\vert) - (\vert \overline p_1 p_3\vert) | ||
| + | </math> <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | \frac{1}{2}\Phi_4 + | ||
| + | \frac{1}{4}(\Phi_5 + \Phi_6) + | ||
| + | \frac{1}{2}(\Phi_1 + \Phi_2) + | ||
| + | \frac{\sqrt2}{4}\Phi_3 | ||
| + | </math> <br> The weights while neglecting overlap are therefore:<br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | 25%\Phi_4 + | ||
| + | 6.25%\Phi_5 + 6.25%\Phi_6 + | ||
| + | 25%\Phi_1 + 25%\Phi_2 + | ||
| + | 12.5%\Phi_3 | ||
| + | </math><br> | ||
| + | |} | ||
| + | |||
| + | |} | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big>'''Computer Exercise'''</big> | ||
| + | |- | ||
| + | | | ||
# Computation of allyl cation energies and weights : | # Computation of allyl cation energies and weights : | ||
## Compute a VBSCF wave function for allyl cation (6-31G basis set) using your selected set of structures (questions 1.3 and 2.2). Compute a VBSCF wave function including the complete set of VB structures, using the '' "str=full" '' keyword. Compare the weights and energies for both wave functions to validate your selection of structures. | ## Compute a VBSCF wave function for allyl cation (6-31G basis set) using your selected set of structures (questions 1.3 and 2.2). Compute a VBSCF wave function including the complete set of VB structures, using the '' "str=full" '' keyword. Compare the weights and energies for both wave functions to validate your selection of structures. | ||
| Ligne 473 : | Ligne 577 : | ||
## We want to build a wave-function corresponding to only one ''Lewis'' structures for the allyl cation. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated to this covalent bond. Propose a selection of ''VB'' structures which would describe one ''Lewis'' structure for the allyl cation. | ## We want to build a wave-function corresponding to only one ''Lewis'' structures for the allyl cation. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated to this covalent bond. Propose a selection of ''VB'' structures which would describe one ''Lewis'' structure for the allyl cation. | ||
## Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl cation at the BOVB level. | ## Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl cation at the BOVB level. | ||
| − | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !'''Answer''' | ||
| + | |- | ||
| + | | | ||
| + | ====''Computation of allyl cation energies and weights''==== | ||
| − | + | # The total energy of the VB wave function with selected set of structures for allyl cation is summarized in the following Table: | |
| + | |||
| + | <center> | ||
| + | {| border="1" | ||
| + | |+ VB energies of the allyl cation | ||
| + | ! scope="col" | Structures & Method | ||
| + | ! scope="col" | Total Energy (au) | ||
| + | |- | ||
| + | ! scope="row" | 3 cov + 1 ionic (VBSCF) | ||
| + | | -116.10652003 | ||
| + | |- | ||
| + | ! scope="row" | Str=full (VBSCF) | ||
| + | | -116.10767709 | ||
| + | |- | ||
| + | ! scope="row" | 3 cov + 1 ionic (BOVB) | ||
| + | | -116.14182494 | ||
|} | |} | ||
| + | </center><br>The energy difference is -0.72 kcal/mol within the VBSCF. Comparison of VBSCF with BOVB both when only using the selected subset, one gets a difference of -22.15 kcal/mol<br><center> | ||
| + | {| border="1" | ||
| + | |+ Weights of the VB structures of the allyl cation | ||
| + | ! scope="col" | | ||
| + | ! scope="col" | Str=full (VBSCF) | ||
| + | ! scope="col" | 3 cov + 1 ion (VBSCF) | ||
| + | ! scope="col" | 3 cov + 1 ion (BOVB) | ||
| + | |- | ||
| + | ! scope="row" |<math> \phi_1 </math> 1:10 11 12 | ||
| + | | 0.31366 || 0.31915 || 0.30595 | ||
| + | |- | ||
| + | ! scope="row" | <math> \phi_2 </math> 1:10 12 13 | ||
| + | | 0.31366 || 0.31915 || 0.30595 | ||
| + | |- | ||
| + | ! scope="row" | <math> \phi_3 </math> 1:10 11 13 | ||
| + | | 0.19911 || 0.19723 || 0.20652 | ||
| + | |- | ||
| + | ! scope="row" | <math> \phi_4 </math> 1:10 12 12 | ||
| + | | 0.15690 || 0.16448 || 0.18158 | ||
| + | |- | ||
| + | ! scope="row" | <math> \phi_5 </math> 1:10 11 11 | ||
| + | | 0.00833 | ||
| + | |- | ||
| + | ! scope="row" | <math> \phi_6 </math> 1:10 13 13 | ||
| + | | 0.00833 | ||
| + | |}</center><br>when comparing 3 cov + 1 ion with Str=full we see that the weights of the last two structures in the second calculation (the more comprehensive calculation) are indeed very small. | ||
| + | <br> | ||
| + | |||
| + | ===='' Resonance energies of allyl cation ''==== | ||
| + | #The following are the three possible structures of allyl cation which describe one Lewis structure:<br>[[File:Allyl_Cation_Lewis.png|450px]]<br> | ||
| + | #The total energy of the VB wave function of the Lewis structure of allyl cation | ||
| + | <br> | ||
| + | |||
| + | {| border="1" | ||
| + | |+ Total energies and weights of the Lewis structure of the allyl cation | ||
| + | ! scope="col" | | ||
| + | ! scope="col" | VBSCF | ||
| + | ! scope="col" | BOVB | ||
| + | |- | ||
| + | ! scope="row" | Total energy (au) | ||
| + | | -116.045854 || -116.0645573 | ||
| + | |- | ||
| + | ! scope="row" | weight of <math> \Phi_1 </math> | ||
| + | | 0.74056 || 0.66590 | ||
| + | |- | ||
| + | ! scope="row" | weight of <math> \Phi_2 </math> | ||
| + | | 0.03291 || 0.05006 | ||
| + | |- | ||
| + | ! scope="row" | weight of <math>\Phi_3 </math> | ||
| + | | 0.22654 || 0.28404 | ||
| + | |||
| + | |} | ||
| + | <br> | ||
| + | * At the BOVB level the resonance energy (RE) of the allyl cation is a difference between the total energy of the allyl radical with full set of the structure and the total energy of the Lewis structure only. RE is 48.49 kcal/mol. | ||
| + | |} | ||
| + | |||
| + | |} | ||
| + | [[VBFile 2-4 | FILES FOR Exercise4]] | ||
| + | |} | ||
| + | |||
| + | |||
[[General_guidelines_for_BOVB_calculations| >> general guidelines for BOVB calculations]] | [[General_guidelines_for_BOVB_calculations| >> general guidelines for BOVB calculations]] | ||
Dernière version du 18 janvier 2013 à 15:56
VB applications on PI systems
In all the following exercises, <math>\pi</math> the system will be taken as active, and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule. The excersise involves calculation of all the electrons. Yet, in principle the <math>\sigma</math> system could aslo be frozen by using the bfi option. Thus, such inputs/outputs are also given however, to avoid redundency, the results from these inputs are not summarized.
| Main exercises | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Exercise 1 : The allyl radical
Exercise 2 : Radical character of ozone
|
| Optional Exercises - Homework | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Exercise 3 : Resonance energy of Benzene
Exercise 4 : The allyl cation
|