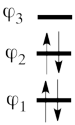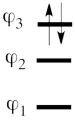Différences entre les versions de « VBTutorial2 »
| Ligne 326 : | Ligne 326 : | ||
| | | | ||
- It is useful to use here the electron hole equivalence for details consult: | - It is useful to use here the electron hole equivalence for details consult: | ||
| − | [[The electron-hole equivalence|>> '' | + | |
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<small>''' The electron-hole equivalence '''</small> | ||
| + | |- | ||
| + | | | ||
| + | In the present case, this equivalence can be used to transform a problem of 4-orbital determinants into a simpler problem of 2-orbital determinants. | ||
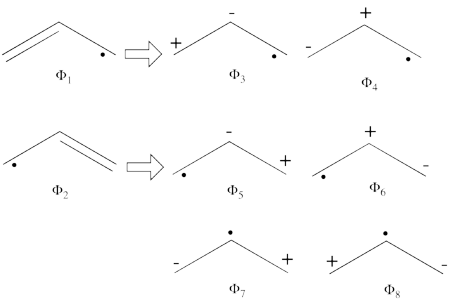
| + | This goes as follows. Whether we reason in the MO framework or in the VB framework, the basis set of orbitals is made of 3 spin-up spinorbitals and 3 spin-down ones. So for each 4-e determinant involving 4 occupied spin-orbitals, we can define a 2-hole determinant involving 2 spin-orbitals, filled with « holes ». Holes have spins and can be represented by up or down arrows just like electrons. There is a one-to-one correspondence between the electron-determinants and the hole-determinants, as shown below : | ||
| + | <br> | ||
| + | <br> | ||
| + | <center> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! electron-filled determinants !! !! hole-filled determinants | ||
| + | |- | ||
| + | |- | ||
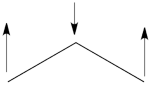
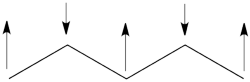
| + | | [[File:electron-trick.png|75px]] || || [[File:hole-trick.png|75px]] | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> || <=> || <math>\vert \varphi_3\bar{\varphi_3}\vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | Expand into || || Expand into | ||
| + | |- | ||
| + | |- | ||
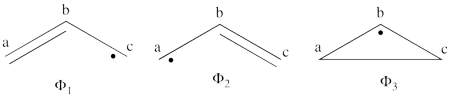
| + | | <math> \Phi_{\textrm{1}}= \frac{1}{\sqrt2}(\vert p_1\overline p_1p_2\overline p_3\vert + \vert p_1\overline p_1p_3\overline p_2\vert </math> || <=> || <math> \frac{1}{\sqrt2}(\vert p_2\overline p_3 \vert + \vert p_3\overline p_2\vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \Phi_{\textrm{2}}= \frac{1}{\sqrt2}(\vert p_3\overline p_3p_1\overline p_2\vert + \vert p_3\overline p_3p_2\overline p_1\vert </math> || <=> || <math> \frac{1}{\sqrt2}(\vert p_1\overline p_2 \vert + \vert p_2\overline p_1\vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \Phi_{\textrm{3}}= \frac{1}{\sqrt2}(\vert p_2\overline p_2p_1\overline p_3\vert + \vert p_2\overline p_2p_3\overline p_1\vert </math> || <=> || <math> \frac{1}{\sqrt2}(\vert p_1\overline p_3 \vert + \vert p_3\overline p_1\vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \Phi_{\textrm{4}}= \vert p_1\overline p_1p_3\overline p_3\vert </math> || <=> || <math> \vert p_2\overline p_2 \vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \Phi_{\textrm{5}}= \vert p_1\overline p_1p_2\overline p_2\vert </math> || <=> || <math> \vert p_3\overline p_3 \vert </math> | ||
| + | |- | ||
| + | |- | ||
| + | | <math> \Phi_{\textrm{6}}= \vert p_2\overline p_2p_3\overline p_3\vert </math> || <=> || <math> \vert p_1\overline p_1 \vert </math> | ||
| + | |} | ||
| + | </center> | ||
| + | <br> | ||
| + | So instead of expanding the Hartree-Fock electron determinant <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> into VB structures, which is complicated, we better expand the smaller complementary hole-determinant <math>\vert \varphi_3\bar{\varphi_3}\vert </math> into VB structures where each contains two holes. Once this is done, it suffices to use the table above to go back to the 4-electron VB structures (e.g. <math> \vert p_2\overline p_2 \vert </math> => <math> \vert p_1\overline p_1p_3\overline p_3\vert </math> and so on). This latter transformation gives us the final 4-e VB function. | ||
| + | |} | ||
| + | |||
| + | {| class="collapsible collapsed wikitable" | ||
| + | |- | ||
| + | !<big>'''BLW within GAMESS (Version: MAR-25-2010 R2)'''</big> | ||
| + | |- | ||
| + | | | ||
| + | # The MO orbitals in the Huckel approximation for ozone are: <br> <math> | ||
| + | \varphi_1 = \frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3) </math> <br> <math> | ||
| + | \varphi_2 = \frac{1}{\sqrt2}(p_1 - p_3)</math> <br> <math> | ||
| + | \varphi_3 = \frac{1}{2}(p_1 - \sqrt{2}p_2 + p_3) | ||
| + | |||
| + | </math> <br> <br> A single-determinant MO wavefunction of ozone based on these Hückel orbitals would look as follows: <br> <math> | ||
| + | \psi_{H\ddot{u}ckel} = \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert = | ||
| + | \vert [\frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)][\overline{\frac{1}{2}(p_1 + \sqrt{2}p_2 + p_3)]}[\frac{1}{\sqrt2}(p_1 - p_3)][\overline{\frac{1}{\sqrt2}(p_1 - p_3)]} \vert | ||
| + | |||
| + | </math> <br> However, we can simplify the problem by using the electron/hole equivalence: [[The electron-hole equivalence|>> ''the electron-hole equivalence'']]<br> <br> Thus, we simply replace holes by electrons and vise versa in <math> \psi_{H\ddot{u}ckel} </math> getting a function of <math> {\psi_{H\ddot{u}ckel}}^{hole} </math>, which we will then expande in terms of VB structures. Finally, we will perform the back hole-electron transformation in the VB representation to get the final result. This way we transform a 4e-3c problem into 2h-3c one.<br> <br> <math> | ||
| + | |||
| + | {\psi_{H\ddot{u}ckel}}^{hole} = \vert \varphi_3\bar{\varphi_3}\vert = \frac{1}{4} \vert (p_1 - \sqrt{2}p_2 + p_3)\overline{(p_1 - \sqrt{2}p_2 + p_3)} \vert | ||
| + | |||
| + | </math><br> <br> Expanding into AO determinants, we get:<br> <br> <math> | ||
| + | |||
| + | {\psi_{H\ddot{u}ckel}}^{hole} = \frac{1}{4} (\vert (p_1\overline p_3 \vert + \vert (p_3\overline p_1 \vert) - \frac{\sqrt{2}}{4}(\vert p_1\overline p_2 \vert + \vert p_2 \overline p_1 \vert) - \frac{\sqrt{2}}{4}(\vert p_2\overline p_3 \vert + \vert p_3 \overline p_2 \vert) + \frac{1}{4} \vert p_1\overline p_1 \vert + \frac{1}{4} \vert p_3\overline p_3 \vert + \frac{1}{2} \vert p_2\overline p_2 \vert | ||
| + | |||
| + | </math><br> <br> Doing the electron-hole back transformation, we get: <br> <br> <math> | ||
| + | |||
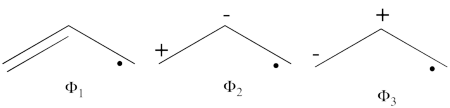
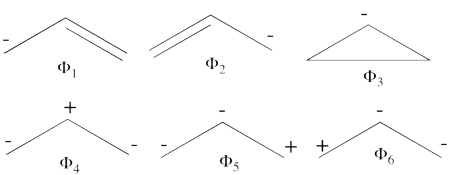
| + | \psi_{H\ddot{u}ckel} = \frac{\sqrt{2}}{4}\Phi_3 - \frac{1}{2}\Phi_1 - \frac{1}{2}\Phi_2 + \frac{1}{4}\Phi_6 + \frac{1}{4}\Phi_5 + \frac{1}{4}\Phi_4 | ||
| + | |||
| + | </math><br> <br> | ||
| + | #The corresponding weights while neglecting overlap (for simplicity) are therefore:<br> <br><math> | ||
| + | |||
| + | \psi_{H\ddot{u}ckel} = | ||
| + | 25%\Phi_1 + | ||
| + | 25%\Phi_2 + 12.5%\Phi_3 + | ||
| + | 25%\Phi_4 + 6.25%\Phi_5 + | ||
| + | 6.25%\Phi_6 | ||
| + | |||
| + | </math><br> <br>Thus, according to simple MO theory the radical character of ozone is 12.5%. | ||
| + | |} | ||
| + | |||
|} | |} | ||
Version du 12 juillet 2012 à 09:46
VB applications on PI systems
In all the following exercises, <math>\pi</math> the system will be taken as active, and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule.
| Main exercises | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Exercise 1 : The allyl radical
Exercise 2 : Radical character of ozone
|
| Optional Exercises - Homework | ||
|---|---|---|
Exercise 3 : Resonance energy of BenzeneComputer Exercise
Exercise 4 : The allyl cation
Computer Exercise
|