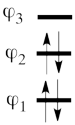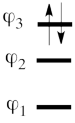VBTutorial2

De Workshops
Aller à la navigation Aller à la recherche

<< Return to the program


How to modify this page :

  • first : log in (top right of this page) ;
  • click on [edit] (far right) to edit a section of the page ;
  • write your text directly in the wiki page, and click on the "Save page" button (bottom left) to save your modifications

Pictures : how to insert a picture in your text

See also this page for an introduction to the basics of the wiki syntax


VB applications on PI systems

Remarks

>> Initial remarks for tutors

Exercices

Remark : in all the following exercises, <math>\pi</math> the system will be taken as active, and the <math>\sigma</math> system as inactive. In all VB calculations, the <math>\sigma</math> orbitals shall be described by MOs delocalized onto the whole molecule.

Main exercises

***** INPUT FILES TO BE WRITTEN *****

Exercise 1 : The allyl radical

Paper Exercises

  1. Covalent structures of the allyl radical :
    1. What are the three possible covalent structures for the allyl radical molecule ? Use the thumb rules of qualitative VB theory to compute their energy, and show that two of them are degenerate.
    2. Show that the third structure can be expressed as a linear combination of the first two structures, and thus that only two of the three covalent structures form a complete basis of non-redundant structures (Rumer basis).
  2. Understanding the pattern of spin density distributions in the allyl radical as found in EPR spectroscpy.
    1. Express the wave functions of the non-redundant structures (from 1.1) of allyl radical in terms of the VB determinant. Write the wave function of the ground state of the allyl radical as a negative combination of the wave functions of the non-redundant structures. Based on the expression of the spin density <math> \rho_s </math>
      <math> {\rho_a}^s = N^2 \sum_i {c_i}^2 {\delta_{ai}}^a</math>

      propose the spin density distribution in the allyl radical. In the above equation N is a normalization constant, c is the coefficient of the VB determinant in the wave function and <math> \delta </math> is either -1 or +1 depending on that electron located on atom a in the ith determinant is <math> \alpha </math> or <math> \beta </math> spin.
    2. Show pictorially:
      1. Why your spin density is polarized.
      2. What would be the spin density pattern in pentadienyl radical?
      3. What would be the spin density in the excited state of allyl radical (taking into account that resulting wave function is a positive combination of the <math> \Phi_L </math> and <math> \Phi_R </math> wave functions?
  3. Covalent and ionic structures of the allyl radical :
    1. What are the possible ionic structures for the allyl radical ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures.


Paper Exercises

  1. Computation of covalent state of allyl radical
    1. Compute the VBSCF wave function for the covalent state of the allyl radical (6-31G basis set) using the covalent structures you have chosen (paper Ex. 1.2). What are the weights of the different VB structures. Was that expected?
    2. What is the wavefunction in determinant description? What is the spin population? Do the calculated results agree with your answer for paper Ex. 2.1?
    3. Repeat the calcultions for the first excited state using "nstate=1" . What is the the wavefunction? Use determinant description. What is the spin population in this case? Was that what you expected?
  2. Computation of allyl radical energy and weights:
    1. Compute a VBSCF wave function for allyl radical (6-31G basis set) using your selected set of structures (questions 1.2 and 3.1). Compute a VBSCF wave function including the complete set of VB structures, using the "str=all" keyword. Compare the weights and energies for both wave functions to validate your selection of structures.
    2. Compute for allyl radical a BOVB wave function which include only your selected set of most chemically meaningful structures (use the guess orbitals obtained at the VBSCF level). Compare the weights obtained at the VBSCF and BOVB level.
  3. Computation of resonance energies :
    1. We want to build a wave-function corresponding to only one Lewis structure for the allyl radical. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated with this covalent bond. Propose a selection of VB structures which would describe one Lewis structure for the allyl radical.
    2. Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl radical at the BOVB level.

>> Answer

Exercise 2 : Radical character of ozone

Paper Exercises

  1. Propose a complete basis of non-redondant VB structures for the ozone molecule. Based on your chemical knowledge, propose a selection subset of the most chemically meaningful structures. (Paper exercise)
  2. Use the HuLis software to retrieve the Hückel MOs for ozone. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures (hint : to make life easier, it may be helpful to use the electron-hole equivalence, described below).
  3. Compute by hand the weights of the different structures (neglecting all overlaps for simplicity). What is the radical character of ozone according to simple MO theory? (Computer exercise)

The electron-hole equivalence


In the present case, this equivalence can be used to transform a problem of 4-orbital determinants into a simpler problem of 2-orbital determinants. This goes as follows. Whether we reason in the MO framework or in the VB framework, the basis set of orbitals is made of 3 spin-up spinorbitals and 3 spin-down ones. So for each 4-e determinant involving 4 occupied spin-orbitals, we can define a 2-hole determinant involving 2 spin-orbitals, filled with « holes ». Holes have spins and can be represented by up or down arrows just like electrons. There is a one-to-one correspondence between the electron-determinants and the hole-determinants, as shown below :

electron-filled determinants hole-filled determinants
Electron-trick.png Hole-trick.png
<math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> <=> <math>\vert \varphi_3\bar{\varphi_3}\vert </math>
Expand into Expand into
<math> \Phi_{\textrm{1}}= \frac{1}{\sqrt2}(\vert p_1\overline p_1p_2\overline p_3\vert + \vert p_1\overline p_1p_3\overline p_2\vert </math> <=> <math> \frac{1}{\sqrt2}(\vert p_2\overline p_3 \vert + \vert p_3\overline p_2\vert </math>
<math> \Phi_{\textrm{2}}= \frac{1}{\sqrt2}(\vert p_3\overline p_3p_1\overline p_2\vert + \vert p_3\overline p_3p_2\overline p_1\vert </math> <=> <math> \frac{1}{\sqrt2}(\vert p_1\overline p_2 \vert + \vert p_2\overline p_1\vert </math>
<math> \Phi_{\textrm{3}}= \frac{1}{\sqrt2}(\vert p_2\overline p_2p_1\overline p_3\vert + \vert p_2\overline p_2p_3\overline p_1\vert </math> <=> <math> \frac{1}{\sqrt2}(\vert p_1\overline p_3 \vert + \vert p_3\overline p_1\vert </math>
<math> \Phi_{\textrm{4}}= \vert p_1\overline p_1p_3\overline p_3\vert </math> <=> <math> \vert p_2\overline p_2 \vert </math>
<math> \Phi_{\textrm{5}}= \vert p_1\overline p_1p_2\overline p_2\vert </math> <=> <math> \vert p_3\overline p_3 \vert </math>
<math> \Phi_{\textrm{6}}= \vert p_2\overline p_2p_3\overline p_3\vert </math> <=> <math> \vert p_1\overline p_1 \vert </math>


So instead of expanding the Hartree-Fock electron determinant <math> \vert \varphi_1\bar{\varphi_1}\varphi_2\bar{\varphi_2}\vert </math> into VB structures, which is complicated, we better expand the smaller complementary hole-determinant <math>\vert \varphi_3\bar{\varphi_3}\vert </math> into VB structures where each contains two holes. Once this is done, it suffices to use the table above to go back to the 4-electron VB structures (e.g. <math> \vert p_2\overline p_2 \vert </math> => <math> \vert p_1\overline p_1p_3\overline p_3\vert </math> and so on). This latter transformation gives us the final 4-e VB function.

|}


Computer Exercises

  1. Compute a VBSCF wave function for ozone (6-31G basis set) using your selected set of structures (question 1.1). Compute a VBSCF wave function including the complete set of VB structures, using the "str=all" keyword. Compare the weights and energies for both wave functions to validate your selection of structures.
  2. Compute a BOVB wave function for ozone which include only your selected set of most chemically meaningful structures (use the guess orbitals obtained at the VBSCF level).
  3. Compare the weights obtained at the VBSCF and BOVB level. Compare the BOVB diradical weight to the value predicted by simple MO theory.

>> Answer

Optional exercises - Homework

Exercise 3 : Resonance energy of Benzene

***** EXERCISE AND INPUT FILES TO BE WRITTEN *****
  1. Covalent only description :
    1. Find what is the complete basis of covalent structures of benzene (hint there should be 5 structures...).
    2. Compute the benzene with str=cov, now repeat the calculation with only 1 of the kékulé strucures and estimate the VRE => too low (reference : 90kcal/mol)
  2. Full description :
    • Ask to compute the benzene with str=full (175 structures)
    • Ask to compute one corresponding Kékulé (27 structures which have to be hand-written !) => good VRE, but cumbersome... We'll see in tutorial 4 that it is more simple with BLW
  • Delocalization problem :
    • Ask people to compute 5 covalent struc. (keyword : "str=cov") first using strictly localized orbitals (VBSCF), then using OEO ('orbtyp=oeo).
    • Compute then 1 kékulé with OEO, and decuce the VRE. It will be much too low, as using OEO implicitly include other struc. than the kékulé, i.e. the individual structures loose their identity => OEO shall not be used to compute diabatic quantities, and more generally if active orbitals are too extended (too large basis set with diffuse functions for instance) diabatic quantities will be wrong (underestimated).


>> Answer

Exercise 4 : The allyl cation


  1. Structures of the allyl cation, and weights from Hückel theory (paper exercise) :
    1. Find a complete basis of covalent structures for the allyl cation.
    2. What are the possible ionic structures for the allyl cation ? Based on your chemical knowledge, propose a selection subset of the most chemically meaningful covalent + ionic structures.
    3. Use the HuLis software to retrieve the Hückel MOs for allyl cation. Write a single-determinant MO wave function based on Hückel orbitals. Develop it into the basis of atomic orbitals, to get an expression in terms of VB structures. Compute by hand the weights of the different structures (neglecting all overlaps for simplicity).

  2. Computation of allyl cation energies abd weights :
    1. Compute a VBSCF wave function for allyl cation (6-31G basis set) using your selected set of structures (questions 1.3 and 2.2). Compute a VBSCF wave function including the complete set of VB structures, using the "str=all" keyword. Compare the weights and energies for both wave functions to validate your selection of structures.
    2. Compute for allyl cation a BOVB wave function which include only your selected set of most chemically meaningful structures (use the guess orbitals obtained at the VBSCF level). Compare the weights obtained at the VBSCF and BOVB level.
    3. Compare the BOVB weights to the weights predicted by simple MO theory.

  3. Computation of resonance energies :
    1. We want to build a wave-function corresponding to only one Lewis structures for the allyl cation. To do so, we will include in the wave-function only one covalent structure, and the ionic structures associated to this covalent bond. Propose a selection of VB structures which would describe one Lewis structure for the allyl cation.
    2. Compute this wave function at VBSCF then BOVB levels. Deduce what is the resonance energy of the allyl cation at the BOVB level.

>> Answer

>> general guidelines for BOVB calculations

Récupérée de « https://wiki.lct.jussieu.fr/workshop/index.php?title=VBTutorial2&oldid=5208 »