Abstracts of the CTTC 2019

<<< CTTC 2019 workshop main page

Slides available after the workshop

HOW TO UPLOAD YOUR ABSTRACT

In order to upload your abstract, you will need a valid login account.

Please contact us email and we will email you your login details.

Please be aware that the whole system has been reinitialized, so old accounts are not valid anymore.

CONTRIBUTORS: please add below, in your own section, your title talk and abstract :

first : log in; (contact the organization for log in details or use the ones we provided in 2014 if you attended Vietnam)
click on your name in the "Contents" box below, this will lead you to your own section;
your section starts with your name as the title line, click on [edit] (far right).
>>> How to insert a picture in your abstract

INVITED SPEAKERS: Please upload your abstracts before 30^st April 2019.
POSTERS: If you wish to contributethe with a poster, feel free to follow the prescribed template in the Poster section . Please upload your abstracts before 30^th April 2019.

All students are strongly encouraged to present a poster at the conference.

Frederik Tielens

Vrije Universiteit Brussel Faculteit Wetenschappen en Bio-ingenieurswetenschappen Pleinlaan 2, B-1050 Brussel, Belgium frederik.tielens@vub.be

Characterization of Self-Assembled Monolayers on Noble Metal Surfaces

Self-assembled monolayers (SAMs) consist of a layer of functionalized long-chain molecules tethered to a solid substrate. SAMs have attracted significant interest of both the fundamental and applied scientific communities. Their presence as a “coating” on a surface is attractive in a number of applications due to the possibility to provide tuning of the surface properties by selectively modifying functional groups on the SAM. Alkanethiols (CH3(CH2)nSH) and alkylthiolate radicals (CH3(CH2)nS∙) adsorption on Au(111) surface is one of the most studied and best-known SAM systems, but also other bioorganic molecules such as amino acids organize at the surface. The nature of the corresponding structure at the surface has been controversial for a long time, as well as other aspects such as the adsorption site on which the thiol chain is anchored, and if the thiol adsorbs by S-H bond breaking process or not. Experimental studies shed some light on both questions, indicating that surface thiol species are attached to Au adatoms, rather than Au atoms in such a bulk-terminated layer, and that it is the movement of these Au-adatom-thiolate moieties that order to produce the SAM structure. Still, some questions remain unsolved such as: At which coverage does this happen, and for which chain length? What is the influence of the presence of defect sites (vacancy and adatoms) on the S-H bond breaking process? The thiols adsorb in a laying down geometry at low coverage, but at which coverage do they straighten up or stand up? In this context we will show here a series of results on the characterization of alkyl thiol SAMs investigated in detail by means of periodic density functional calculations.

References I. Lorenzo Geada, I. Petit, M. Sulpizi and F. Tielens, Surf.Sci. 677 (2018) 271. E. Colombo, G. Belletti, F. Tielens, P. Quaino, Appl. Surf. Sci. 452, (2018) 141. S. Kumar Meena, C. Goldmann, D. Nassoko, M. Seydou, T. Marchandier, S. Moldovan, O. Ersen, F. Ribot, C. Chanéac, C. Sanchez, D. Portehault, F. Tielens, M. Sulpizi, ACS Nano, 11, 7371 (2017). D. Nassoko, M. Seydou, C. Goldmann, C. Chanéac, C. Sanchez, D. Portehault, F. Tielens, Materials Today Chemistry 5, 34, (2017). C. Goldmann, F. Ribot, L.F. Peiretti, P. Quaino, F. Tielens, C. Sanchez, C. Chanéac, D. Portehault, Small, 13, 1604028, (2017) H. Guesmi, N. Luque, E. Santos, F. Tielens, Chem.Eur.J, 23, 1402, (2017). D. Costa, C.-M. Pradier, F. Tielens, L. Savio, Surface Science Reports, 70, 449 (2015).

↑ top of this page

Sam Trickey

Dept. of Physics and Quantum Theory Project, Univ. of Florida

Less is More – or – Back to Kohn-Sham

Simplification of widely used meta-generalized-gradient approximation (mGGA) exchange-correlation functionals by removal of their explicit orbital dependence is valuable because it re-incorporates mGGA calculations in the Kohn-Sham framework. Returning to the pure Kohn-Sham local potential framework (rather than the generalized K-S approach almost always used with orbital-dependent mGGA functionals) aids interpretability and improves computational efficiency in large-scale simulations. The talk will summarize how the Laplacian level of refinement can be achieved by use of suitably constructed approximate kinetic energy density functionals (KEDFs). The existence of Laplacian-level deorbitalizations which yield better performance than the original mGGA will be illustrated for molecules with the meta-GGA-made-very-simple functional. Results on standard molecular and condensed-phase test sets obtained from the deorbitalized version of the SCAN functional (“SCAN-L” for SCAN with Laplacian) reproduce the original SCAN error patterns rather well. However, the magnetization of bcc Fe is quite different, an important distinction that will be discussed.

Supported by U.S. Dept. of Energy grants DE-SC 0002139 and DE-SC 0019330.

References D. Mejía-Rodríguez and S.B. Trickey, Phys. Rev. B 98, 115161 (2018); Phys. Rev. A 96, 052512 (2017).

Adrienn Ruzsinszky

Department of Physics, Temple University, Philadelphia, PA 19122, USA

Going beyond the random phase approximation for materials

The Random Phase Approximation (RPA) has become a standard method beyond semilocal Density Functional Theory (DFT) that naturally incorporates weak interactions and eliminates self-interaction error in the exchange energy [1]. RPA is not completely perfect, however, and suffers from self- correlation error as well as an incorrect description of short-ranged correlation. To improve upon RPA, various beyond-RPA approximations were developed in the past decade. The most familiar approximations are the RPA+ [2], SOSEX (second-order screened exchange) [3] along with model exchange-correlation kernels within the time-dependent DFT framework [4]. Exchange-correlation kernels can be applied to excited states and optical spectra [4]. In this talk I will reveal the strengths and limitations of these methods. In addition, I will introduce new alternative routes which can deliver further improvement beyond the already existing techniques [5,6]. Applications will be also discussed.

Work is supported by NSF DMR–1553022 and DOE BES DE-SC0012575.

References:[1] H. Eshuis, J. E. Bates, F. Furche, Theor. Chem. Acc., 131, 1084 (2012) [2] S. Kurth and J. P. Perdew, Phys. Rev. B, 59, 10461, (1999) [3] A. Grüneis, M. Marsman, J. Harl, L. Schimka, and G. Kresse, J. Chem. Phys. 131, 154115 (2009) [4] J.E. Bates, S. Laricchia, and A. Ruzsinszky, Phys. Rev. B 93, 045119, (2016) [5] T. Gould, J. P. Perdew and A. Ruzsinszky, to be submitted [6] P.D. Mezei, A. Ruzsinszky, to be submitted.

Luis Rincon

Universidad San Francisco de Quito, Quito, Ecuador

The information content of the Fermi and Coulomb holes

This presentation summarizes two recently proposed information quantities which are employed to visualize the Fermi and Coulomb holes in the real space. The first one is the information content of the Exchange-Correlation hole, calculated from the Kullback–Leibler divergence of the same-spin conditional pair density respect to the marginal probability (χXC). As reported, χXC, can be used to reveal the regions of the space associated to the classical electron pair model [1-3]. The second one is the information content of the correlation hole, which is computed in terms of the Kullback–Leibler divergence of a correlated same-spin conditional pair density respect to the uncorrelated Hartree–Fock pair density (χC) [4-5]. These two information quantities are discussed on the light of the results for high-spin clusters of alkali metals.

1. L. Rincon, R. Almeida, P. L. Contreras and F.J. Torres “The information content of the conditional pair probability” Chem. Phys. Lett. 635, 116 (2015). 2. A.S. Urbina, F.J. Torres and L. Rincon “The electron localization as the information content of the conditional pair probability” J. Chem. Phys. 144, 244104 (2016). 3. L. Rincon, F.J. Torres and R. Almeida “Is the Pauli exclusion the origin of electron localization?” Mol. Phys. 116, 518 (2018) 4. L. Rincon, F.J. Torres, M. Becerra, S. Liu, A. Fritsch and R. Almeida “On the separation of the information content of the Fermi and Coulomb holes and their influence on the electronic properties of molecular systems” Mol. Phys. 117, 610 (2019) 5. F.J. Torres, L. Rincon, C. Zambrano, J.R. Mora and M.A. Mendez “A review on the information content of the pair density as a tool for the description of the electronic properties of molecular systems” Int. J. Quantum Chem. 119, e25763 (2019)

Ángel Martín Pendás

Dpto. Química Física y Analítica. Universidad de Oviedo. Oviedo, Spain

Should charge-shift bonding be reconsidered?

Charge-shift bonding (CSB) was introduced as a distinct third family of electron-pair links that adds to the covalent and ionic tradition. However, the full battery of orbital invariant tools provided by modern real space artillery shows that it is difficult to find CSB signatures outside the original valence-bond framework in which CSB was developed. Here we show that this concept should probably be further investigated.

References J. Luis Casals-Sainz, F. Jiménez-Grávalos, E. Francisco, A. Martín Pendás, Chem. Commun. (2019), DOI: 10.1039/C9CC02123J

Dennis R. Salahub

Department of Chemistry, Centre for Molecular Simulation, Institute for Quantum Science and Technology, Quantum Alberta, University of Calgary, Canada

Towards free-energy profiles for nano-catalyzed chemical reactions in complex environments

I will review our attempts to build somewhat realistic models of nanocatalysis at finite temperature. Current thoughts are to bring in machine-learning techniques to, ideally, define the relevant reaction coordinates/collective variables. Significant progress has been made on such questions in the bio- modeling literature and I would like to understand the new ML methodologies better and to, hopefully, adapt them to the field of nanocatalysis. I am a neophyte, eager for any guidance that CTTC participants might offer, once I have exposed my state of knowledge/ignorance.

Josep M. Luis

University of Girona

Density Functional Theory and Nonlinear Optical Properties

The design of new molecular materials with large nonlinear optical properties (NLOP) remains a challenging task for computational chemistry due to the necessity of accurately computing both electronic and vibrational hyperpolarizabilities of individual molecules as well as the effects of intermolecular interactions. Density Functional Theory (DFT) has proven to be a powerful tool for solving various quantum mechanical problems in a cost-effective way, but DFT performance in the area of NLOP has been under active assessment. We have performed an extensive study of the performance of a diverse set of density functional approximations in predicting the NLOP of hydrogen-bonded complexes using the CCSD(T)/aug-cc-pVTZ level of theory as reference.[1] For all the studied properties, the average absolute errors below 20% can only be obtained using the CAM-B3LYP functional, while LC-BLYP and MN15 are shown to be only slightly less accurate. We reported huge errors in predicting the vibrational second hyperpolarizability by B97X, M06 and M06-2X functionals. This large failure is traced down to a poor determination of third- and fourth-order energy derivatives with respect to normal modes. These results reveal serious flaws of some DFT methods and suggest caution in selecting the appropriate functional to calculate any molecular property that contains vibrational anharmonic contributions.

We have also analyzed the optimal tuning of range-separatiod LC-BLYP functional based on adjusting the attenuating function parameters to satisfy ionization potential theorem. Our results revealed that this approach does not bring any systematic improvement in the predictions of NLOPs. However, we have explored new strategies to tune the range-separation parameter to provide a correct description of NLOP, performing an exhaustive study of the dependency of this parameter in terms of simply quantities.[2] We have found a simple expressions for the optimal value of the attenuating parameter in terms of the second hyperpolarizability values computed at LC-BLYP level that reproduce the CCSD(T) second hyperpolarizabilities. The hyperpolarizabilities obtained with our NLOP-tailored new optimal tuned LC-BLYP are more accurate than the ones obtained with CAM-B3LYP and LC-BLYP functionals. .

References [1] Robert Zalesny, Miroslav Medved,Sebastian Sitkiewicz, Eduard Matito, Josep M. Luis, “Can Density Functional Theory Be Trusted for High-Order Electric Properties? The Case of Hydrogen-Bonded Complexes”, J. Chem. Theory Comput., submitted. [2] Pau Besalú, Sebastian Sitkiewicz, Pedro Salvador, Eduard Matito, Josep M. Luis, in preparation.

Joakim Halldin Stenlid

Department of Physics, Stockholm University, Sweden

Chemical interaction behaviour probed by the local electron attachment energy

The ability to make swift and reliable predictions of chemical interaction behavior and reactivity lies at the heart of theoretical chemistry. This presentation will examine the performance of a new DFT-based ground-state property, the local electron attachment energy [E(r)] [1], for the prediction of global and local electrophilicity/Lewis acidity. E(r) is a property based on a multi-orbital analysis of the unoccupied KS-DFT electronic states. It is found that this joint-orbital picture outperforms the frontier molecular orbital approach (FMO) for predictions of both regioselectivity and intermolecular reactivity trends. E(r) furthermore complements the electrostatic potential probe by reflecting also local contributions to charge-transfer and polarization. Examples of the use of E(r) are taken from molecular reaction theory including conjugate addition and aromatic substitution, as well as from materials science with emphasis on heterogeneous catalysis of transition metal and transition metal oxide nanoparticles and surfaces [2]. Comparisons are made to both experimental and computational data. Future directions for the efficient screening of new catalytic materials based on the new property will be discussed.

References

[1] T Brinck, P Carlqvist, JH Stenlid, Local Electron Attachment Energy and Its Use for Predicting Nucleophilic Reactions and Halogen Bonding, The Journal of Physical Chemistry A 120, 10023-10032, 2016 [2] T Brinck, JH Stenlid, The Molecular Surface Property Approach: A Guide to Chemical Interactions in Chemistry, Medicine, and Material Science, Advanced Theory and Simulations, 2, 1800149, 2019

Juan E. Peralta

Department of Physics, Central Michigan University, Mount Pleasant MI 49959

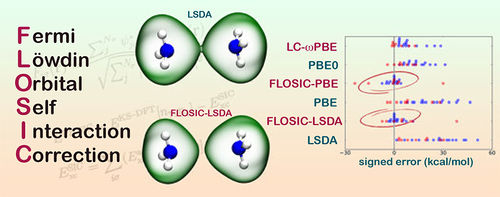
The FLO-SIC route to self-interaction-free DFT

The effect of DFT self-interaction error (SIE) on calculated molecular and solid-state properties has been known for a long time. The most widely accepted framework for removing SIE in DFT is due to Perdew and Zunger (PZ) [1]. However, due to the high computational cost associated with minimizing the PZ energy expression, the calculation of explicitly self-interaction free molecular properties remains elusive. Recently, an efficient implementation for SIE removal based on Fermi orbitals was proposed [2]. This method explicitly avoids the unitary transformation from canonical to localized orbitals that is needed in standard PZ, and replaces it by a Fermi-Löwdin transformation which depends only on one vector descriptor per orbital, or Fermi orbital descriptor (FOD). The Fermi-Löwdin orbital self-interaction correction (FLO-SIC) provides an computationally efficient alternative to the traditional PZ methods. [2] I will describe the FLO-SIC methodology and its advantages and caveats compared to PZ-SIC. I will show our recent efforts to make FLO-SIC more efficient and user-friendly. [3] As an illustration of the capabilities of the FLO-SIC method, I will show some recent results of diverse properties in cases where SIC is important and discuss the opportunities to move FLO-SIC forward.[4-6]

References

[1] J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
[2] M. R. Pederson, A. Ruzsinszky, and J. P. Perdew, J. Chem. Phys. 140, 121103 (2014).
[3] K. Trepte, S. Schwalbe, T. Hahn, J. Kortus, D. Kao, Y. Yamamoto, T. Baruah, R. R. Zope , K. P. K. Withanage, J. E. Peralta, and, K. A. Jackson, J. Comp. Chem. 40, 820 (2019).
[4] K. P. K. Withanage, K. Trepte, J. E. Peralta, T. Baruah, R. Zope, and Koblar A. Jackson, J. Chem. Theory Comput. 14, 4122 (2018).
[5] R. P. Joshi, K. Trepte, K. P. K. Withanage, K. Sharkas, Y. Yamamoto, L. Basurto, R. R. Zope, T. Baruah, K. A. Jackson, and J. E. Peralta, J. Chem. Phys. 149, 164101 (2018).
[6] K. Sharkas, L. Li, K. Trepte, K. P. K. Withanage, R. P. Joshi, R. R. Zope, T. Baruah, J. K. Johnson, K. A. Jackson, and J. E. Peralta, J. Phys. Chem. A 122, 9307 (2018).

Emmanuel Fromager

Université de Strasbourg, Laboratoire de Chimie Quantique, Institut Le Bel, 4 rue Blaise Pascal, 67000 Strasbourg, FRANCE

Density matrix functional embedding theory based on the Householder transformation

In the increasingly popular density matrix embedding theory (DMET) [1], a fragment (also referred to as impurity) of the full electronic system of interest is embedded into an effective reduced-in-size environment (referred to as bath). A Schrödinger-like equation can then be solved accurately (if not exactly) for the embedded cluster (impurity+bath). Despite the name of the method, the embedding procedure of standard DMET essentially relies on a state-specific and approximate (mean-field) wavefunction. Consequently, its improvement as well as its extension to finite temperatures is not straightforward.

In this talk, I will present an in-principle-exact DMET-like approach where the embedding is fully driven by the (one-electron reduced) density matrix. In such a density matrix functional embedding theory (DMFET), the bath is determined by applying a Householder transformation to the density matrix [2]. The method is in principle systematically improvable since electron correlation in the (so-called Householder) cluster environment is described by a functional of the density matrix. Exact and approximate single-impurity formulations of DMFET will be presented for the one-dimensional Hubbard model. Extensions to multiple impurities and connections with standard DMET will also be discussed.

References

[1] G. Knizia and G. K.-L. Chan, Phys. Rev. Lett. 109, 186404 (2012). [2] M. Saubanère, L. Mazouin, M. Tsuchiizu, and E. Fromager, in preparation (2019).

Daniel Finkelstein-Shapiro

Department of Chemical Physics, Lund University, Sweden

Constructing effective operators for open quantum systems using ancillary continua

Sommaire

Frederik Tielens

Sam Trickey

Adrienn Ruzsinszky

Luis Rincon

Ángel Martín Pendás

Dennis R. Salahub

Josep M. Luis

Joakim Halldin Stenlid

Juan E. Peralta

Emmanuel Fromager

Daniel Finkelstein-Shapiro

Thibault Terencio

Mark E. Tuckerman

Speaker 15

Speaker 16

Speaker 17

Speaker 18

Speaker 19

Speaker 20

Speaker 21

Speaker 22

Speaker 23

Menu de navigation

Rechercher