Abstracts of the Kathmandu Workshop 2012

Newari art

The abstracts are in the alphabetical order of the author names.

Helen van Aggelen

Ghent University

Variational optimization of second order density matrices for chemistry

A myriad of ab initio methods uses simple mathematical objects to describe a chemical system in order to avoid the ‘exponential wall’ inherent to the wavefunction. This talk evaluates the use of variational second order density matrix methods for chemistry and identifies the major theoretical and computational challenges that need to be overcome to make it successful for chemical applications.

Its major theoretical challenges originate from the need for the second order density matrix to be N-representable: it must be derivable from an ensemble of N-electron states. Our calculations have pointed out major drawbacks of commonly used necessary N-representability conditions, such as incorrect dissociation into fractionally charged products and size-inconsistency, as well as flaws in the description of spin properties. We have derived subspace energy constraints that fix these problems, albeit in an ad-hoc manner.

Its major computational challenges originate from the method’s formulation as a vast semidefinite optimization problem. We have implemented and compared several algorithms that exploit the specific structure of the problem. Even so, their slow speed remains prohibitive. Both the second order methods and the zeroth order boundary point method that we tried performed quite similar, which suggests that the underlying problem responsible for their slow convergence, ill-conditioning due to the singularity of the optimal matrix, manifests itself in all these algorithms even though it is most explicit in the barrier method.

Significant progress in these two areas is needed to make the variational second order density matrix method competitive to comparable wavefunction based methods.

Vishwanath P. Agrawal

Constituent Assembly of Nepal

Theoretical Chemistry in Nepal

Developmental history of theoretical chemistry and its branches spanning a period of almost 110 years will be briefly presented.The status of theoretical chemistry which was included in the Tribhuvan University curriculum in 1969 will be described. Factors affecting its satisfactory growth will be discussed.

Gloria Mazzone, Marta E. Alberto, Nino Russo and Emilia Sicilia

Università della Calabria

[trans-Ru(PMe₃)₂(H₂O)₄]²⁺ catalyzes H₂ production by selective decomposition of formic acid

Hydrogen has attracted increasing attention as an alternative secondary energy resource. Being the efficient storage and handling of hydrogen one of the major obstacles to its use for energy applications, extensive research has been carried out to develop novel materials for hydrogen gas storage and liberation,although no entirely satisfactory options have been found so far. An attractive alternative that can contribute to reduce CO₂ emissions is the use of CO₂ itself as a hydrogen carrier [2]. Actually, based on formic acid and carbon dioxide, a sustainable and reversible cycle for energy storage can be conceived by storage of hydrogen in formic acid and release from it. As shown in a recent work, formic acid (HCOOH) decomposes selectively to afford H₂ and CO₂ in presence of a catalytic amount of a water-soluble, trans-Ru(tppts)₂(H₂O)₄]²⁺ , ruthenium aqua complex, in a solution of HCOOH/HCOONa 9:1 [3]. A tentative catalytic cycle has been proposed by the authors on the basis of NMR experiments. To gain more insight into the mechanism of dehydrogenation of formic acid by ruthenium and to accomplish a full elucidation of the proposed catalytic cycles, including the characterization of relevant transition states and short-life intermediates, we have undertaken a Density Functional Theory (DFT) study of formic acid decomposition catalyzed by the trans-Ru(PMe₃)₂(H₂O)₄]²⁺ complex. We first investigated the mechanism proposed by Laurenczy and co-workers. Next, alternative reaction routes were explored on the basis of computational evidences.

[1] a) D.L. Royer, R.A. Berner, J. Park, Nature, 446, 2007, 530; b) N.S. Lewis, D. G. Nocera, Proc. Natl. Acad. Sci. USA, 103, 2006, 15729.

[2] a) S. Enthaler, ChemSusChem, 1, 2008, 801; b) F. Joò, ChemSusChem, 1, 2008, 805.

[3] C. Fellay, N. Yan, P. J. Dyson, G. Laurenczy Chem. Eur. J., 15, 2009, 3752.

Paul Ayers

McMaster University

What Should One Do When Electronic Structure Methods Aren’t Good Enough? Machine-Learning Methods for Molecular Properties

Thermodynamic properties like equilibrium and rate constants are exquisitely sensitive to errors in the relative free energies of the chemical species involved. For example, experimental measurements of acidity in molecules and proteins are often accurate to .1 pKa unit; in order to compute pKa’s to this accuracy, one must compute the Gibbs free energy of deprotonation to within .5 kJ/mol (2 × 10–4 a.u.). This level of computational accuracy is inaccessible for small molecules in the gas phase and unfathomable for large molecules in solution.

Fortunately, the errors in computational models tend to be systematic. It is thus possible to correct the errors in the computations with statistical methods. This talk will show how a hybrid approach, wherein computational models are reparameterized to agree with experimental data, can provide computational models for pKa’s that approach experimental accuracy. The primary tools are multiple regression (with great care taken to avoid overfitting); the residual errors can be removed, at least in part, using a machine learning method called Gaussian process regression (kriging). These methods are applied to a diverse set of acids, including molecular acids (carboxylic acids, alcohols, and amines) and proteins. While experimental accuracy is not attainable, root-mean-square errors that are significantly less than one pKa unit are attainable.

Daniel Borgis

CNRS and Ecole Normale Supérieure

Classical Density Functional Theory and its Application to Chemistry

We will ask how the concepts developed for electronic DFT in quantum chemistry and classical DFT in statistical mechanics can nourish from each other and lead to a practical application of classical DFT to problems of chemical interest: Molecular solvation, complex interfaces, molecular recognition, ...

Benoît Braida

Université Pierre et Marie Curie

How VB theory can help to understand multicenter bonding

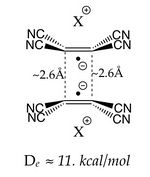
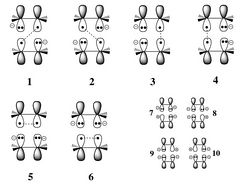
In this talk it will be shown how simple VB analysis could shed light on multicenter bonding, in the prototype case of ditetracyanoethylene dianion dimer π-[TCNE]22–. Analysis of the VB wave function shows that the essential physics of the multicenter bonding is captured by a very simple description in terms of only six Valence Bond structures. It is confirmed that the inter-fragment bonding interaction is not a simple two-electron bond between the two fragments, each of these structures being repulsive by itself even at the qualitative VB level, so all the bonding comes from the resonance. It is shown that the fragments are held together by a resonating combination of classical 3-e bonds, a type of bond that has been described for the first time by Pauling in 1931. This model is confirmed by accurate ab initio mixed Valence Bond / Quantum Monte Carlo calculations, and explains at the same time : 1) the long but strong bond, 2) the almost constant bond distance between the two monomers whatever the environment, 3) the importance of dynamic correlation in these systems.

[1] Pauling, L. J. Am. Chem. Soc. 1931, 53, 3225

>> slides of this talk

Ria Broer

Zernike Institute for Advanced Materials

First principles Studies of Magnetic Interactions in Molecules and Solids

An important task for Theoretical Chemistry is to develop and apply methods for the accurate computation of electronic and magnetic properties of molecules and solids, to complement experimental observations. An equally important task is to analyze the accurate results, therewith enabling interpretation in terms of useful physical and chemical concepts. In the case of magnetic interactions we have now gained much experience with the prediction of relative energies and electron distributions of states with different electron spin couplings. The results are often conveniently interpreted in terms of phenomenological spin hamiltonians, like the Heisenberg Hamiltonian that includes only isotropic couplings, which can be extended with anisotropic terms in case the latter turn out to be important. The mechanisms of transitions between one spin state and another as occur for example in light induced excited-spin state trapping (LIESST) are still not well understood, but current research is devoted to this problem. In this contribution I will give an overview of methods used to approach the scientific problems mentioned above and discuss their merits and limitations.

Patrick Bultinck with Andres Cedillo, Dimitri Van Neck, Paul W. Ayers

Ghent University

Understanding properties of conceptual DFT quantities using simple algebraic tools

One of the main successes of chemistry has been that using a set of so-called chemical concepts one can rationalize and even predict chemical observations. Many of these concepts were even introduced relatively long before the introduction of quantum mechanics. Many have survived up to present day, often without having been rethought in the light of a quantum chemical theory under the "excuse" that one does not need to replace that which was not broken. Yet, mainly thanks to the development of density functional theory and especially so-called conceptual DFT, the attitude has changed and a decent framework is sought for chemical concepts such as electronegativity, hardness, ... and a theoretical basis established for theorems such as electronegativity equalization.

Unfortunately, one often finds that once the pioneers properly defined the chemical concepts and put it in quantum mechanical perspective, attention to detail and proper proof weakens in favour of mere use of the concepts. This causes a drop in rigour or at least the degree to which rigour is attempted.

This talk shows, using a simple set of mainly algebraic manipulations, how rigour can be recovered quite easily for some debated issues like the possibility of negative Fukui functions in a molecule [1] and the justification of quadratic expansions of the energy in electronegativity equalization [2]. This leads to a more fundamental understanding of the chemical concepts and may provide rich new insights in the theories.

[1] Bultinck, P.; Clarisse, D.; Ayers, P.W., Carbo-Dorca, R. The Fukui matrix: a simple approach to the analysis of the Fukui function and its positive character. Phys. Chem. Chem. Phys., 2011, 13, 6110–6115. Bultinck, P.; Van Neck, D.; Acke, G.; Ayers, P.W. Influence of electron correlation on the Fukui matrix and extension of frontier molecular orbital theory to correlated quantum chemical methods. Phys. Chem. Chem. Phys., 2012, 14, 2408 - 2416.

[2] Cedillo, A.; Van Neck, D.; Bultinck, P. Self-consistent methods constrained to a fixed number of particles in a given fragment and its relation to the electronegativity equalization method. Accepted for publication, Theor. Chem. Acc., 2012.

>> slides of this talk

Carlos Cárdenas

Universidad de Chile

Navigating the Hard-Soft Acids-Bases Principle.

Hard-soft acids-bases (HSAB) principle of Pearson establishes that when the strength of the acids and bases involved in the reaction is similar, hard acid prefer binding to hard bases an soft acids prefer binding to soft bases. For years the hardness of molecules lacked of a mathematical definition and a numerical scale of hardness was unavailable. However, in 1983 Parr and Pearson identified the hardness as the derivative of electronic chemical potential (the Lagrange multiplier in Euler equation of DFT) with respect to the number of electrons. This definition orders correctly the hardness of molecules and it is in agreement with many physical properties empirically associated to hardness. Nevertheless, there is not a complete proof of HSAB in terms of this definition of hardness. Such proof seems impossible as HSAB operates differently in different reactions. However, much can be learned and proofed when one studies relevant cases. I will review most of available theoretical evidence in favor of HSAB and, significantly, recent contributions we have done in understanding the validity of HSAB in a situation as general as can be double exchange acid-base reactions. Both, mathematical proofs and Monte Carlo-like experiment will be shown.

Stephane Carniato

Université Pierre et Marie Curie

How RIXS and theory can be combined to measure the electronegativity

Polarization-dependent resonant inelastic x-ray scattering (RIXS) is a new probe [1] of molecular-field effects on the electronic structure of isolated molecules. A combined experimental and theoretical analysis explains the linear dichroism observed in Cl 2p RIXS following Cl 1s excitation in HCl due tomolecular-field effects, including singlet-triplet exchange, indicating polarized-RIXS provides a direct probe of spin-orbit-state populations applicable to any molecule. It will be shown how theory-experiments can be helpful to predict the electronegativity of radical species and why it is challenging for a better description of the chemical bond in core excited species.

Guanhua Chen

University of Hong Kong

Penetrating Potential Barrier One Hundred Percent

It is known that a quantum particle may tunnel through a potential barrier. However, the overall transmission coefficient is less than one. We consider an infinite chain of atoms. Applying an external field to raise the potential energy of a few atoms in the middle, we find that under certain condition an incoming electron may go through the potential barrier completely. Numerical simulation of transient current, evaluating of steady state current and as well as analytic result of a model system will be present. The precise condition for such a complete tunneling will be discussed.

Henry Chermette

Université Lyon1

The Gradient-Regulated Connection of Generalized Gradient Exchange Functionals: Interest and Limitations

The Gradient-Regulated Connection (GRAC) has been introduced a few years ago by Baerends et al. in order to build a density functional potential model satisfying theoretical conditions and providing Kohn-Sham orbitals. Recently the GRAC has been used to build an exchange functional able to mix performances of a modified PBE for the bulk region, to those of the PW91 for the asymptotic one. This exchange functional, coupled with the TCA correlation functional, was able to significantly improve the modeling of weak interacting systems, while keeping a good accuracy for the atomization energies. The interest and the limitations of this approach is discussed.

Jerzy Cioslowski

University of Szczecin

All you always wanted to know about many-electron harmonium atoms

Recent theoretical and numerical developments on electronic structures of harmonium atoms with more than two electrons are reviewed, including FCI and Monte Carlo results, as well as a new accurate representations for the total energy and its components in terms of a transformed coupling strength.

Gerardo Delgado Barrio

Instituto Física Fundamental (CSIC)

Theoretical studies of Helium clusters doped with diatomic molecules

Spectroscopic studies of simple molecules surrounded by He atoms show a drastic difference depending on the fermionic or bosonic character of the solvent atoms [1]. A quantum chemistry-like approach has been developed in our group to deal with HeN –BC doped helium clusters, where the BC dopant is a conventional di-atomic molecule. The central idea is to consider the He atoms as “electrons” while the B and C atoms play the role of the nuclei in standard electronic structure calculations. The procedure provides spectral simulations and, hence, making feasible to do proper comparisons with current experiments (1). However, due to the big difference of masses of He and electrons, and also to the replacement of Coulomb potentials by molecular interactions, it is worthy to asses at what extent the approximations involved (decoupling of orbital angular momenta of the He atoms from the BC rotation and adiabaticity of the BC stretch versus de He motions) lead to accurate results (2-6). Here, we consider several diatomic molecules as dopants. The model provides the energy levels of the cluster and the intensities of the main lines of the spectrum at low temperatures (7-9).

[1]S. Grebenev,J. P. Toennies, and A. F. Vilesov, Science 279, 2083 (1998)

[2]D. López-Durán,M. P. de Lara-Castells, G. Delgado-Barrio,P. Villarreal, Di Paola,F. A. Gianturco, and J. Jellinek, Phys. Rev. Lett. 93,053401 (2004). J. Chem. Phys. 121, 2975 (2004)

[3]M. P. de Lara-Castells, D. López-Durán,G. Delgado-Barrio, P. Villarreal, C. Di Paola,F.A.Gianturco,and J. Jellinek Phys. Rev. A 71, 033203 (2005)

[4] M.P. de Lara-Castells, R. Prosmiti, G. Delgado-Barrio, D. López-Durán, P. Villarreal,F.A.Gianturco, and J. Jellinek, Phys. Rev. A 74, 053201 (2006)

[5]M. P. de Lara-Castells, R. Prosmiti, D. López-Durán, G. Delgado-Barrio, P. Villarreal, F. A. Gianturco, and J. Jellinek, Int. J. Quant. Chem.107, 2902 (2007)

[6]O.Roncero,R.PérezdeTudela,M.P.deLara-Castells,R.Prosmiti, G. Delgado-Barrio, and P. Villarreal,Int.J.QuantumChem.107(2007)2756. J.Chem. Phys. 128,164313(2008)

[7] O. Roncero, M.P. de Lara-Castells, G. Delgado-Barrio, P. Villarreal, T. Stoecklin, A. Voronin, and J.C. Rayez J. Chem. Phys. 128 (2008)164313, M. P. de Lara-Castells, P. Villarreal, G. Delgado-Barrio, and A. O. Mitrushchenkov. J. Chem. Phys. 131 (2009) 194101,R. Prosmiti, G. Delgado-Barrio, P. Villarreal, Ersin Yurtsever, Emanuele Coccia and Franco A. Gianturco J. Phys. Chem. A 113 (2009) 14718

[8]M. P. de Lara-Castells, N. F. Aguirre, P. Villarreal, G. Delgado-Barrio, and A. O. Mitrushchenkov, J. Chem. Phys. 132 (2010) 194313,

[9]R. P´ EREZ DE TUDELA, D. L´OPEZ-DUR´ AN, T. GONZ´ ALEZLEZANA, G. DELGADO-BARRIO, P. VILLARREAL, F. A. GIANTURCO, and E. YURTSEVER J. Phys. Chem. A 115, 6892 (2011)

Etienne Derat

Université Pierre et Marie Curie

Models for complex bioinorganic systems: a tool for future design?

Enzymes are fascinating molecular objects, designed by nature to perform chemical reactions with high turn-over, regioselectivity and stereoselectivity. Therefore, they represent a "Holy Grail" for most bio-organic chemists. But when a metal is included in the enzymatic structure, they also represent a difficult challenge for theoretical chemists: most if not all force-fields were designed for organic only species, QM methods are not always robust with transition metals, and sometimes to add even more difficulties, reactions are performed in the excited state, or with open-shell wavefunctions. In our days, solving such a problem has been in some way tackled: choose your favorite QM/MM scheme, and run CCSD(T)/CASPT2/MRCI/BOVB calculations on top of it. But modeling a chemical system is not only choosing the best (and most expensive) calculations, modeling is creating a tool that can be used by others to understand/design/play with their own chemically related systems. In this talk, archetypical enzymatic systems will be shown that illustrate the fact that rationalizing them using theoretical chemistry tools can help to design new structures with improved functionalities or new chemical reactivities.

John Dobson

Griffith University

Dispersion Forces

The dispersion energy is a long-ranged part of the correlation energy, but there are many ways to understand it. A summary will be given of various approaches to the theory of dispersion forces, including some very old and some very new ones.

Matthias Ernzerhof

University of Montreal

Non-Hermitian quantum mechanics and density functional theory

A simple model for electron transport through molecules is provided by the source-sink potential (SSP) method [F. Goyer, M. Ernzerhof, and M. Zhuang, JCP 126, 144104 (2007)]. In SSP the boundary conditions of having an incoming and outgoing electron current are enforced through complex potentials that are added to the Hamiltonian, resulting in a non-Hermitian theory. Similarly, complex absorbing potentials (CAPs) have proven to be useful tools in the theory of metastable states. Various existing electronic structure theories are not suitable for systems described by a non-Hermitian Hamiltonian. We discuss the recently developed complex-density functional theory (CODFT) [Y. Zhou, M. Ernzerhof, JCP 136, 094105 (2012)], which extends the Kohn-Sham method to the realm of non-Hermitian systems. Applications of this method to electron transport through molecules and to the calculation of the lifetime of metastable systems are presented. CODFT calculations might benefit from the development of completely non-local functionals of the electron density and we propose such approximations.

Thomas Frauenheim

University of Bremen

DFTB - Recent methodological extensions, applications and challenges

In the last years, we have developed an approximate Density Functional Theory Method (SCC-DFTB), which can be derived from DFT by a second order expansion of the total energy expression with respect to the charge density [1].The scheme is characterized by (i) the use of a limited, usually minimal basis, (ii) a two-center approximation for the Kohn-Sham Hamiltonian, (iii) a second-order functional expansion of the total energy and (iv) the simplification of two-electron integrals in the Mulliken approximation.

Improvements of the original scheme include a modification of the treatment of electron-electron repulsion terms for a better description of hydrogen bonded systems and inclusion of third order terms in the density fluctuations, which become important for the treatment of highly charged systems [2]. Recently, we have used a new scheme to derive repulsive potentials, which increases the accuracy substantially, but also shows the limits of the current method [3]. Since common DFT-GGA functionals lack the description of dispersion forces, which is inherited by SCC-DFTB, we have included them empirically because of their crucial role for the stability of protein and DNA structures [4]. SCC-DFTB has been further implemented into combined quantum mechanical molecular mechanical (QM/MM) algorithms and has been widely applied to biological systems, in particular to proton transfer reactions. The scheme has been extended into various mutlti-scale approaches, where the QM/MM method is coupled to an electrostatic treatment of the environment [5].

Additionally, recent advances in the development of the time-dependent density functional based tight-bind method (TD-DFTB) will be summarized [6]. The range of validity of these approximations is assessed by comparison to first principles time-dependent density functional theory (TDDFT) calculations in converged basis sets. Within the TD-DFTB framework, several strategies to solve the time-dependent Kohn-Sham equations are discussed. These include a linear response treatment in the frequency domain, direct propagation in the time domain leading to an O(N) scheme and an implementation for open boundary conditions, suitable for applications in molecular electronics.

[1] Elstner et al., PRB 58 (1998) 7260

[2] Elstner, JPCA 111 (2007) 5614. , Yang et al., JPCB, 111 (2007) 10861.

[3] Gaus et al., JPCA 2009, 113, 11866; Z. Bodrog et al.J. Chem. Theory. Comput. 7 (2011) 2654

[4] Elstner et al.,JCP. 114 (2001) 5149

[5] Cui et al. JPCB 105 (2001) 569

[6] T. A. Niehaus, J. Mol. Structure-THEOCHEM 914 (2009) 38

Patricio Fuentealba

Universidad de Chile

The richness of the dynamic of clusters and molecules

Ab initio molecular dynamics for a variety of atomic clusters and molecules will be shown and discussed. In systems as small as M3 (M= alkali metal atom) there are some interesting phenomena like pseudorotation and transposing. The dynamics will be characterized by some geometric parameters and also energetic considerations. In some cases, especially Na7 , it was also possible to identify a transition state for the conversion between the two main isomers. In molecules of the type MCN (M: alkali metal atom) it will be shown how the alkali metal atom orbits around the cyano ion. Using the same type of dynamics we also simulated some reactive collisions producing new exotic molecules.

Andreas Görling

University of Erlangen-Nuremberg

The adiabatic-connection dissipation-fluctuation theorem as route to a new generation of density-functional methods: perspectives and challenges

The adiabatic-connection dissipation-fluctuation theorem provides a a rigorous basis for constructing correlation functionals for density-functional methods within the Kohn-Sham formalism. In the simplest case the correlation energy within the direct random phase approximation is obtained. By considering besides the Coulomb kernel also the exact frequency- dependent Kohn-Sham exchange kernel in the construction of the correlation functional, methods with an unprecedented robustness and accuracy are obtained. Systems that are problematic or not accessible for standard density- functional methods can be handled. For example, electronic structures characterized by static correlation can be treated as well as Van-der-Waals interaction. On the other hand, challenges like higher computational effort or questions of numerical stability come along with these new approaches. The current status, the pros and cons, possible future developments, and the general perspectives of approaches based on the adiabatic-connection dissipation-fluctuation theorem are discussed.

Irek Grabowski

Nicolaus Copernicus University, Torun

Impact of the correlation effects on the KS DFT potentials, energies and densities.

Direct comparison of the correlation potentials, electron densities and correlation energies, generated from few variants of correlated Optimized Effective Potential Method (OEP), standard Density Functional Theory (DFT) and from ab initio Wave Function Theory Methods (WFT), has been employed for analyzing the impact of the correlation effects on those quantities. These methods have been applied to a few atomic and molecular systems.

The correlation potentials, energies and densities generated from correlated OEP - OEP2-sc [1], OEP-ccpt2 [2] and from WFT methods - Coupled Cluster and second-order Many Body Perturbation Theory show very similar and systematic behaviour, reconfirming the correctness of the ab initio DFT (OEP2) methods [3,4].

In a contrast it has been demonstrated that the VWN5 and LYP correlation functionals do not represent any substantial correlation effects on the KS-correlation potentials [3,4] and electron density [5], whereas these effects are well represented by the orbital dependent OEP correlation functionals. In the same time for the local, generalized-gradient, and hybrid functionals it has been found that the dynamic correlation effects are to a large extend accounted for by densities resulting from exchange-only calculations. Additional calculations with self-interaction corrected exchange potentials indicate that this finding cannot be explained as an artifact caused by the self-interaction error or non dynamic correlation effect.

The usefulness of such kind of analysis in a context of development new exchange correlation functionals in DFT will be also discussed.

Manoj K. Harbola

Indian Institute of Technology, Kanpur

Energy functionals for excited-states

In this talk we present a systematic approach to developing energy functionals for excited-state DFT calculations. These functionals are derived by splitting the k-space for homogeneous electron gas and give very accurate results. Response function analysis shows why splitting k-space could be the method of choice for constructing energy functionals for excited-state calculations.

Frank E. Harris

University of Florida

Fully Correlated Wavefunctions for Small Atoms

While this work includes a lot that is new, I would expect to give a talk that is general enough to place the new developments in the context of the line of work that was started by Robert Hill and was advanced significantly by Rebane (St. Petersburg), with some further contributions from our laboratory and from others.

Trygve Helgaker

University of Oslo

Density-functional theory in magnetic fields

I intend to discuss the universal density functional with emphasis on magnetic fields—in particular in relationship to the Lieb variation principle. We have generalized our scheme for the calculation of the universal density functional by Lieb maximization from full configuration interaction (FCI) wave functions to electrons in magnetic fields. As a first step, we will study the density functional in a finite field without introducing a current dependence, simply regarding the charge density as the conjugate to the scalar potential with a parametric dependence on the magnetic field. Subsequently, we intend to study the charge and current densities as conjugate to the scalar and vector potentials. Different formulations of the universal density functional in magnetic fields will be discussed.

Philippe Hiberty

Université de Paris 11

Valence Bond Theory and Reactivity: Correlation Between the Diradical Character of 1,3-Dipoles and their Reactivity Toward Ethylene and Acetylene.

Preliminary summary: The influence of the diradical character of 1,3-dipoles on the barrier to 1,3-dipolar cycloaddition is studied by means of ab initio valence bond theory. Each 1,3-dipole is described as a linear combination of three valence bond structures, two zwitterions and one diradical. The diradical character of 1,3-dipoles is shown to be a critical feature to favor 1,3-dipolar cycloaddition. Within each family of 1,3-dipoles, involving diazonium betaines, nitrilium betaines and azomethine betaines, a linear relationship is evidenced between the weight of the diradical structure in the 1,3-dipole and the barrier to cycloaddition to ethylene or acetylene. The barrier heights also correlate with the transition energies from ground state to pure diradical states of the 1,3-dipoles at equilibrium geometry. From these results, we propose a reaction mechanism in which the 1,3-dipole first distorts so as to reach a “reactive electronic state” that has a significant diradical character, then adds with little or no barrier to the dipolarophile. This mechanism is in line with the recently proposed distortion/interaction energy model of Ess and Houk2 and their finding that the barrier heights for the cycloaddition of a given 1,3-dipole to ethylene and acetylene are nearly the same, despite the exothermicity difference.

Nasarul Islam and Altaf Hussain Pandith

University of Kashmir

Antimicrobial activity assessment of certain anilide derivatives; a DFT study

Several physiochemical, structural and quantum-mechanics based descriptors were derived for a set of anilide derivatives, using DFT-B3LYP/6-311G (d, p) level of theory. The aim of this study was to develop QSAR model using multiple linear regression to predict the antimicrobial activity of anilides towards E. Coli in terms of several electronic and molecular descriptors. The best-fit model involved electrophilicity index (ω) in conjunction with molecular weight (W) and logarithm of the octanol-water partition co-efficient (Log P) as antimicrobial activity descriptors. A comparison of the QSARs [ pIMC = -2.163 E_LUMO+ 0.050 log P + 0.81, R²_adj = 0.738, RSS = 0.109, F = 110.743], [ pIMC= 0.058 ω + 0.047 Log P+ 0.772, R²_adj = 0.771, RSS =0.095, F= 132.361], [ pIMC = -0.088ELUMO+ 0.012 α + 0.248, R²_adj = 0.688, RSS = 0.129, F = 87.307] and [ pIMC = 0.053ω +0.011α + 0.253, R²_adj = 0.722, RSS = 0.115, F = 102.235] suggesting that ω is marginally a better descriptor than ELUMO and Log P is slightly a superior descriptor than α for parameterization of electrophilic reactivity and hydrophobicity of molecules respectively.

References: 1. Okuma K., Iwakawa K., Turnidge J.D., W. B. Grubb W.B., Bell, J.M., O’Brien F.G., Coombs G.W., Pearman J.W., Tenover F.C., Kapi M., Tiensasitorn C., Ito, T. and Hiramatsu, K. 2002, J. Clin. Microbiol. 40, 4289

2. Klei E., Smith D.L. and Laxminarayan R. 2007, Emerg. Infect. Dis. 2007,13, 1840

3. Johnson E. M., Warnock D. W., Luker J., Portor S. R. and Crispian S. J. 1995, Antimicrob. Chemother. 35, 103

4. Emami S., Foroumadi A., Falahati M., Loffali E., Rajabalian S., Ebrahimi S.A., Farahyar S. and Shafiee A. 2008, Bioorg. Med. Chem. Lett. 18,141

5. Ozawa I., Takeuchi I., Yamomoto K., Hamada Y., Ito, T., Kuwahara M., and Takagaki T.1984, Chem. Pharm. Bull., 32, 305

B. Kaderiya^{1, 2}, Bhadra P. Pokharel³, R. K. Thapa⁴ and M. P. Ghimire^2,5

¹Central department of physics, Tribhuvan University, Kritipur, Nepal ² Nepal Academy of Science and Technology, Khumaltar, GPO Box: 3323, Kathmandu, Nepal ³ Department of Physics, Institute of Engineering, Tribhuvan University, Pulchowk, Lalitpur,Nepal ⁴ Department of Physics, Mizoram University, Tanhril- 796009, Aizawl, Mizoram, India ⁵ WPI Center for Materials Nanoarchitectonics (MANA), National Institute for Materials Science (NIMS), Tsukuba, Japan

First Principles density functional theory: A relevant tool for calculating electronic and magnetic properties of materials

Density functional theory (DFT) is an undisputed workhouse for the present day first principles electronic and magnetic properties calculations. It considers electron charge density ρ(r) as basic entity and rigorously demonstrates that ground state properties of an interacting electronic system can be computed provided charge density is known. For materials like double perovskites (A₂B’B’’O₆), DFT enlightens electronic and magnetic properties via computational approach with efficiency. A computational work on double perovskites (Ba₂TmNbO₆) based on DFT is presented. In this work, full-potential linearized augmented plane wave (FP-LAPW) method is applied to perform first principles total energy calculations. To take into account the exchange and correlation potential, GGA method is used. Computation had been done by using WIEN2k code .

Deba Bahadur Khadka

Tribhuvan University and Tokyo Institute of Technology

Optical model calculation of the total Penning ionization cross sections of Ne(3P1) by O2

Collisional deexcitation of excited rare gas atoms by atoms and molecules is of great importance in both fundamental and applied sciences, which provides the essential features of chemical reactions, in particular, those including electronic energy transfer [1-4]. The collisional deexcitation is a key also to understand fundamental processes in the interaction of ionizing radiation with matter and the phenomena in ionized gases [3-5]. In the present investigation, the quantum mechanical calculation of the total Penning ionization cross sections for Ne(3P1) by O2 have been reported as a function of the mean collisional energy using an optical potential model. The experimental cross sections for the deexcitation of Ne(3P1) by O2, CO2 and CH4 as a function of the mean collisional energy are shown in Figure 1. The deexcitation cross sections of Ne(3P1) are in the range of 23-28 Å2 for O2, 49-61 Å2 for CO2 and 10-24 Å2 for CH4, respectively. The cross sections are dependent on the present target molecules; the cross sections for O2 are slightly larger than those for CH4 but smaller than those for CO2. The behavior of the collisional energy dependence of the cross sections for CH4 is slightly different from those for O2 and CO2; the cross sections increase slightly with increasing the collisional energy for CH4, whereas for O2 and CO2 those are nearly constant as a function of collisional energy. The experimental cross sections for the deexcitation of Ne(3P1) by O2 are compared with the values calculated using optical model considering with and without electron exchange interaction, namely, between diex and di, respectively, as well as semi-classical approach (see Figure 2). The comparison of the experimental results with theoretical justifies the deexcitation of resonant Ne(3P1) atoms dominated by an electron-exchange interaction rather than dipole-dipole interaction. Details will be discussed at the workshop.

References

1. A. Niehaus, Adv. Chem. Phys., 45 (1981) p.399; in Physics of Electronic and Atomic Collisions, ed. by S. Datz, Amsterdam, North-Holland, 1982, p.237.

2. A. J. Yencha, in Electron Spectroscopy-Theory, Techniques and Applications, ed. by C. R. Brundle and A. D. Baker, Academic, New York, 5 (1984), p.197.

3. M. Ukai and Y. Hatano, in Gaseous Electronics and Its Applications, ed. by R. W. Crompton, M. Hayashi, D. E. Boyd and T. Makabe, KTR Scientific Publishers, Tokyo, 1991, p.51.

4.Y. Hatano, in Pulse Radiolysis, ed. by Y. Tabata, CRC Press, Boca Raton, 1991, p.199.

5. D. B. Khadka, Y. Fukuchi, M. Kitajima, K. Hidaka, N. Kouchi, Y. Hatano and M.Ukai, J. Chem. Phys., 107 (1997), 2386.

Leeor Kronik

Weizmann Institute of Science

Understanding photoelectron spectroscopy from first principles - progress and challenges

Preliminary summary: In this talk, I will discuss the pros, cons, progress made, and remaining limitations, of understanding photoelectron spectroscopy with density functional theory, using semi-local, conventional hybrid, and range split hybrid functionals. This will be achieved via judicious comparison with experiment and with the results of many-body perturbation theory calculations.

Wenjian Liu

College of Chemistry and Molecular Engineering, Peking University

The `Big Picture' of Relativistic Molecular Quantum Mechanics

Relativistic Molecular Quantum Mechanics (RMQM) as the union of Relativistic Quantum Chemistry (RQC) and Quantum Electrodynamics (QED) consists of three components (i.e., Hamiltonian, wave function, and property), each of which is confronted with some fundamental issues, including, e.g., 'What is the appropriate relativistic many-electron Hamiltonian?'[1,2], 'How to make explicit and/or local representations of relativistic wave functions?'[1,3,4], 'How to formulate relativistic properties?'[5], 'How to interface RQC and QED?'[1], etc. In this lecture I shall try to address these fundamental issues from both conceptual and methodological standpoints, so as to establish the `big picture' of RMQM[6].

1. W. Liu, Perspectives of relativistic quantum chemistry: The negative energy cat smiles, Phys. Chem. Chem. Phys. 14, 35-48 (2012).

2. W. Liu, Ideas of relativistic quantum chemistry, Mol. Phys. 108, 1679-1706 (2010).

3. Z. Li, S. Shao, and W. Liu, Relativistic explicit correlation: Coalescence conditions and practical suggestions, J. Chem. Phys. 136, 144117 (2012). 4. F. Wu, W. Liu, Y. Zhang, and Z. Li, Linear-scaling time-dependent density functional theory based on the idea of `from fragments to molecule', J. Chem. Theor. Comput. 7, 3643-3660 (2011).

5.Y. Xiao, Q. Sun, and W. Liu, Fully relativistic theories and methods for NMR parameters, Theor. Chem. Acc. 131, 1080-1-17 (2012).

6. W. Liu, The `big picture' of relativistic molecular quantum mechanics in AIP proceedings Volume: "Theory and Application in Computational Chemistry. The First Decade of the Second Millennium", edited by E. Clementi, et al. (Sept., 2012).

Jean-Paul Malrieu

Université de Toulouse

Scale changes and reduction of the degrees of freedom in wave-function calculations through contraction and real space renormalization techniques

Post-mean field calculations in principle have to work in a Hilbert space of huge dimension. Two tools should enable us to reduce this size problem.

The first one consists in contracting sets of excitations into a composite vector. Multi-reference CI approaches, either perturbative or variational, frequently make use of such contractions, the form of which is very flexible. Other methods may contract excitations from topological criteria, using a unique vector for the excitations from the same couple of occupied localized MOs, or from the same region of space.

The second strategy is based on the concept of Real Space Renormalization. It divides the space into blocks and builds the wave function in a reduced space, composed of products of low energy eigenstates of the blocks. The energies of the block states and of their interactions is evaluated from accurate calculations on block pairs or triads, through effective Hamiltonian theory. Such a strategy may be used to compute excitation energies of large or infinite periodic systems in a Renormalized Excitonic Method, which represents a local approach to delocalized excitations.

Alexis Markovits

Laboratoire de Chimie théorique UMR7616 UPMC/CNRS

THE ACTIVE ROLE OF THE SURFACE IN HETEROGENEOUS CATALYSIS

Reaction mechanisms studies in heterogeneous catalysis have been focusing on adsorbate’s behavior for many years. However, in recent years, the role of the surface itself has been emphasized. “Modern surface science techniques have shattered the myth of the rigid surface waiting for the reaction to occur [1], the molecule adsorbing strongly, reacting and desorbing.

Particle shape, size and faceting are already a proof of that. In my talk, I present several examples of the active role of the surface. Surface flexibility during hydrogenation processes is a key feature of catalysts. Ethylidyne is shown to have a crucial role even if it does not directly participate to the catalytic process. Being strongly bound, it remodels the active site. It moves on the metal surface allowing a high turnover. Even though this mobility has been evidenced, it contains an apparent contradiction with the strength of the binding between the adsorbate and the surface. Another very large surface reorganization is due to oxygen. Oxygen yields pinholes on the surface which are mandatory for catalysis.

Ángel Martín Pendás

Universidad de Oviedo. Spain

Fluctuation of electron populations and chemical bonding.

An interesting description of chemical bonds is emerging from the study of the fluctuations of the electron population in real space domains. The latter include the atoms of the Quantum Theory of Atoms in Molecules (QTAIM), as well as the different attraction basins of the Electron Localization Function (ELF). These lecture will present a didactic model of chemical bonding in an N-electron, m-nuclei molecule in terms of the probabilities of the different statistical events coming from distributing N balls in m cages.

>> slides of this talk

Christian Minot

LCT, UPMC, ParisVI

Reducibility of metal oxides

The properties of metal oxides depend on the reducibility of the metal cation. When the cation oxidation states vary, the adsorption takes place on another site with a different force. The dissociation of H2 on reducible oxides is different from that of irreducible ones. We analyze the mechanisms of formation of gaps and O hydrogenation that reduces oxides. When the cations are reducible, they are the seats of the reduction. When the cations are not, the electrons are localized in the cavity, trapped by the Madelung field. The formation of the vacancy is more costly in energy and reduced the surface more reactive. The analysis is supported by VASP calculations.

Om Prakash Niraula

Tribhuvan University

Survey of literature on mathematical chemistry

A brief survey of literature on mathematical chemistry is presented. This contribution draws attention to the literature in the areas of development on mathematical chemistry. Mathematical modelling in chemistry begins in the early primary grades even though the language and ideas of mathematical modelling are not employed. Further, this literature survey on mathematical chemistry provides guidelines for researchers. The survey concludes theoretical feedbacks in mathematical chemistry.

Anna Okopinska

Jan Kochanowski University

Entanglement in natural and artificial atoms and molecules.

The recent progress in nanoscale technology made possible to address single quantum objects. Very small clusters containing down to a few atoms, molecules or ions can be isolated in various kinds of electromagnetic and optical traps at ultracold temperatures. Apart of nature-made atoms and molecules, the artificial few-body quantum systems become available, such as superconducting circuits or semiconductor quantum dots, that can be also individually addressed. The correlation effects are crucial for determining the properties of such systems. Especially useful is the concept of entanglement which refers to the correlations that have no classical counterpart. The problem of measuring entanglement is very complex and different methods have been proposed for its quantification. I will review several measures that are being used to quantify entanglement in few-body systems and discuss their behavior for simple models of natural and artificial quantum systems.

Sourav Pal

National Chemical Laboratory

Coupled cluster theory: stationary or non-stationary?

The coupled cluster theory has been viewed primarily as a non- stationary theory and is often formulated as a similarity-transformed form of the Hamiltonian. However, in this presentation, it will be shown that it is possible to have explicit stationary forms of this theory, which are more useful for various properties. There exist many alternate stationary forms of the theory. The merits and demerits of several such forms will be discussed and the new developments from our group will be presented.

Mario Piris

University of the Basque Country

Can NOFT bridge the gap between DFT and WFT?

Since the molecular Hamiltonian operator contains only one- and two-electron operators, the energy of a molecule can be determined exactly from the knowledge of the one- and two-particle reduced density matrices (1- and 2-RDMs). The most accurate electronic structure methods are based on N-particle wave functions. Given an N-particle wave function, we have the N-RDM, and by contraction the 1- and 2-RDMs can be derived. Unfortunately, the N-particle wave-function is a too complex object and its manipulation becomes cumbersome as the system grows larger. In 1964, Hohenberg and Kohn demonstrated that the ground state energy can be expressed as a functional of the one-electron density only. The density functional theory (DFT) has become very popular thanks to its relatively low computational cost. In the exact DFT, we should reconstruct the 1- and 2-RDMs from the density, however, most practical implementations of DFT are based on the Kohn-Sham formulation, in which the kinetic energy is not constructed as a functional of the density but rather from an auxiliary Slater determinant. The contribution from a part of the kinetic energy in the correlation potential is probably the main source of problems of present-day KS functionals. Another obstacle is the construction of a functional capable of describing the N-particle system. This functional N-representability is related to the N-representability of the 2-RDM. Even though DFT energies may lie quite close to the exact ones, it is not fully guaranteed not to be below the exact ones, as required by the variational principle. In 1974, Gilbert proved for the 1-RDMs an analogous theorem to the Hohenberg-Kohn theorem for the electron density. He suggested an alternative viewpoint regarding 1-RDM functional theory. One can employ the exact functional with an approximate 2-RDM that is built from the 1-RDM using a reconstruction functional. The major advantage of a 1-RDM formulation is that the kinetic energy is explicitly constructed and does not require a functional. Like for the density, the ensemble N-representability conditions of the 1-RDM are well-known, but naturally, this does not overcome the N-representability problem of the energy functional. The 1-RDM functional is called Natural Orbital Functional (NOF) when it is based upon the spectral expansion of the 1-RDM. A reconstruction of the 2-RDM has been achieved using the cumulant expansion leading to an approximate NOF known in the literature as PNOF. The PNOF is based on an explicit ansatz of the two-particle cumulant λ(Δ,Π) satisfying the D-, Q- and G-necessary positivity conditions for the 2-RDM. In this presentation, the theory behind the PNOF is outlined. Special emphasis will be put on the spin conserving NOF theory and on the recent proposed algorithm which yields the natural orbitals by an iterative diagonalization of a generalized pseudo-Fockian matrix. Some examples of strongly correlated systems, where density functionals yields pathological failures, are also presented to illustrate the potentiality of the NOF theory.

Claire C. Ralph

Cornell University

Time Evolution of Matrix Product States and its Application to NMR

Abstract missing

Nino Russo

Università della Calabria

How to choose the exchange-correlation potential for different systems or processes: menu à la carte ou menu du jour ?

In the last decade many new exchange-correlation functionals have been proposed and tested. Looking at the applications it seems that the best way to work is to choose the exchange-correlation functional on the basis of the system of the physical process under investigation. Establishing criteria could be useful to people that live in this Babel in order to avoid the philosophy of “one problem one XC”.

Dennis R. Salahub

University of Calgary

Electron transfer and other reactions in proteins – towards an understanding of the effects of quantum decoherence

We have embarked on a multistage research program on the multiscale theory, simulation, computation and understanding of electron transfer and other reactions in complex bio-systemsi.

Our entry into the fieldi was our recent tunneling pathway analysis on molecular dynamics simulations of the methylamine dehydrogenase (MADH)—amicyanin (Am) redox pair. We found that the most frequently occurring molecular configurations afford superior electronic coupling, via a hydrogen-bonded “water bridge” between donor and acceptor. Surface residues are crucial to the recognition and dynamic docking of the proteins as well as the organisation of the aqueous environment at the active site, increasing the lifetime of the water bridge. Mutant complexes fail to achieve the same bridge stability.

A second contributionii reports our first attempts to understand the effects of quantum decoherence on the rates of chemical reactions. Multiple-state reaction rates can be estimated within semi-classical approaches provided the hopping probability between the quantum states is taken into account. This probability is intimately related to the transition from the fully quantum to the semi-classical description, but this issue is not adequately handled with kinetic models commonly in use that so far have treated this transition only in a perturbative manner. Quantum nuclear effects like decoherence and dephasing are not present in the rate constant expressions. Retaining the intuitive semi-classical picture, we included these effects through the introduction of a phenomenological quantum decoherence function. In addition to the electronic coupling term, a characteristic decoherence time tdec now also appears as a key parameter of the rate constant. The introduction of this new dimension may imply profound changes to our understanding of chemical reactivity. The new formula has been tested by means of Density Functional Theory molecular dynamics simulations for a triplet to singlet transition within a copper dioxygen adduct and for an electron-transfer model involving a Li donor and a Li+ acceptor, separated by up to five peptide units. We are now setting up to re-examine the MADH-Am with this new method, hence avoiding the empiricism of the pathway model.

W. H. Eugen Schwarz

Tsinghua U Beijing & U Siegen Germany

Descriptive and Explanative Concepts of Theory for Chemistry

The basic experimental facts of chemistry are reproducible by numerical physical theory – chemistry is reducible to physics. The basic concepts and rules of chemistry are fuzzy constructs weakly related to two-valued logics – chemistry is an ‘autonomous’ science. Theoretical Chemistry has three aims: i) Predict or improve or corroborate the numerical facts; ii) Work out the details not easily obtainable experimentally, thereby refining the description of the individual facts; iii) Underpin or develop chemically useful and fruitful concepts and rules that lead to an intuitive understanding and explanation of the phenomena. Some discussion in chemistry may become more fruitful upon accounting for these conceptual differences. Five points may help towards softer discussions. (1) The construction of theoretical concepts should be guided by both, physical rigor (such as, e.g. in QTAIM) and the aim of recovering the notions that have been found chemically fruitful (such as, e.g. the various types of primary and secondary bond-interactions). (2) Partitioning the chemical phenomena into elementary physical steps should not only consider the stationary initial and final states (such as in QTAIM or NBO approaches) but also include non-stationary intermediate states that exhibit the physically characteristic internal relaxation mechanism. (3) Even if sufficiently accurate, the partitioning into large contributions of opposite sign is less valuable for a qualitative chemical understanding, as long as the trend of one big decisive term or sum of terms cannot be made obvious (e.g. on the basis of the variation principle - or by chemical intuition). (4) Causal explanatory notions, even if more vague or fuzzy than some more rigorous and unique descriptive concepts, must be advanced towards fruitful chemical theory. (5) The analysis of real though seemingly paradoxical relaxation mechanisms in chemical and physical processes helps towards a better understanding of scientific as well as sociological phenomena.

Peter Schwerdtfeger

Massey University Auckland

High Pressure Simulations – Squeezing the Hell out of Atoms

The pressure range accessible to laboratory experiments exceeds now a remarkable 20 orders of magnitude, from ultra-high vacuum (< 1 nPa) to ultra-high pressures (> 100 GPa). With the development of high-pressure diamond-anvil cells we are now able to study materials at pressures equivalent to the pressure at the centre of our earth (350 GPa). In other planets and stars pressures beyond the TPa range are reached, which can only be explored by thermonuclear explosions or by theoretical methods. At high pressures unusual structures and materials properties are observed. It is, however, a formidable task to accurately derive equations of state (EOS), f(P,V,T)=0, and corresponding phase diagrams, for gases, liquids and the solid state up to high pressures and temperatures from first principles, that is from quantum theory and statistical physics. Our research group has just achieved that recently for neon, where the isotherms are in excellent agreement with experimental data. Fundamental questions we are currently exploring are, for example, if we can already understand the density-pressure relationship of simple atomic crystals (like helium or neon) from squeezing atoms. Is the EOS virial equation applicable for mercury in the gas phase? Can we obtain accurately melting temperatures up to the high-pressure range? Moving to more complex systems, we present new results on optical properties of ice under pressure, which is important for understanding the physics of icy planets. And finally, can we model the melting of mercury using first principle methods? Mercury is a notoriously difficult element to treat by quantum theoretical methods as not only electron correlation effects but also relativistic effects need to be considered, and the many-body expansion of the interaction energy between mercury atoms does not converge in the overlap region of the interaction.

Gustavo E. Scuseria

Rice University

Symmetry breaking & restoration

We derive and implement symmetry-projected Hartree-Fock-Bogoliubov (HFB) equations and apply them to the molecular electronic structure problem. All symmetries (particle number, spin, spatial, and complex conjugation) are deliberately broken and restored in a self-consistent variation after-projection approach. We show that the resulting method yields a comprehensive black-box treatment of static correlations with effective one-electron (mean-field) computational cost. The ensuing wave function is of multireference character and permeates the entire Hilbert space of the problem. The energy expression is different from regular HFB theory but remains a functional of an independent quasiparticle density matrix. All reduced density matrices are expressible as an integration of transition density matrices over a gauge grid. We present several proof-of-principle examples demonstrating the compelling power of projected quasiparticle theory for quantum chemistry.

Tomasz Wesolowski

University of Geneva

Joining seamlessly microscopic and macroscopic levels of description of matter: challenges and perspectives for modelling methods based on Frozen-Density Embedding Theory.

We target static properties of embedded systems. Using the formal framework of Frozen-Density Embedding Theory as the basis for numerical simulations of the multilevel type, hinges on a number of approximations, assumptions or even conjunctures of universal or system-specific nature. They will be overview taking into account our understanding of Frozen-Density Embedding Theory and numerical experience accumulated so far.

Henryk Witek

National Chiao Tung University

Exact solution of Schrodinger equation for helium: Where are we?

Modern quantum chemistry is built upon exact solutions to the Schrodinger equation for the simplest chemical system, hydrogen atom. In that way the dynamic correlation between the electrons is neglected in the first approximation, requiring quite sophisticated mathematical methods to recover it (usually only partially) in the afterward treatment. It is clear that it would be advantageous to build quantum chemical apparatus from models incorporating exactly the electron correlation, e.g., the helium atom.

A poll conducted in the community of quantum and computational chemists shows that most of the respondents consider the helium problem unsolvable and simultaneously are not able to point out any proof of this fact. The review of existing literature, however, suggests the contrary... The present talk is supposed to summarize the current state of knowledge about the solution of the Schrodinger equation for the ground state of the helium atom and to discuss its future perspectives.

Khumbu Icefall seen from the Everest Base Camp

SLIDES: